二分类评估器-----ROC以及AUC【含python实现】

2019.06.30晚
下周四面试nlp，顺便复习一下机器学习

A

引：以正负标签为例，在正负样本均衡情况下，单纯的使用准确率即可。但如果样本正负分布极端不平衡，这将导致准确率很高但实际模型效果很差的情况。比如预测地震，1000个地质状态里面可能只有一个将发生地震，模型直接全部预测为不发生那么准确率为100%，但效果很差。因此单纯准确率有时是不可信的！！！

B

sample：{P, N} 样本集合 P(positive)，N(negative)，假设 10 , 3
FP: N中被分类器预测为正样本的个数 ；TP：P中被分类器预测为正样本的个数
ROC曲线的
横坐标是FPR(false positive rate)假阳性率；
纵坐标是TPR真阳性率
$\{\begin{array}{l}FPR=FP/N\\ TPR=TP/P\end{array}$
可以看出 ，ROC考虑的是预测的正样本的分布情况。一般情况下，模型预测是根据所得概率与设置的概率阈值相比较从而输出类别。比如sigmod函数以0.5为例
所以模型实际输出的情况是由你所设置的阈值决定，我们人为的从0到1设置阈值，将得到一个完整的ROC曲线

为方便理解先用两个极限描述一下
当阈值为1的时候，预测结果都是负的（FP == TP == 0）所以ROC点为（0,0）
但阈值为0的时候，预测结果都是正的（FP == N,TP == P）所以ROC点为（1,1）
以图为例

样本序号	真实标签	模型输出概率
1	p	0.9
2	p	0.8
3	n	0.7
4	p	0.6
5	p	0.55
6	p	0.54
7	p	0.51
8	n	0.35
9	n	0.53
10	p	0.48

实现代码如下【有点初级…没看sklearn源码】

y = np.array([1,1,0,1,1,1,1,0,0,1]);y = y.tolist()
P = [i for i,x in enumerate(y) if x == 1]
N = [i for i,x in enumerate(y) if x == 0]
probs = np.array([0.9,0.8,0.7,0.6,0.55,0.54,0.51,0.35,0.21,0.17])
threesholds = np.array([0.0,0.2,0.35,0.4,0.61,0.77,1.0])
ROC = []
for i in threesholds:
    p_index = []
    n_index = []
    for idx,prob in enumerate(probs):
        if prob >= i:
            p_index.append(idx)
        else:
            n_index.append(idx)
    tp = 0;fp = 0
    for k in p_index:
        if k in P:
            tp += 1
    for k in p_index:
        if k in N:
            fp += 1

    roc = [fp/len(N),tp/len(P)]
    ROC.append(roc)
ROC = np.array(ROC)

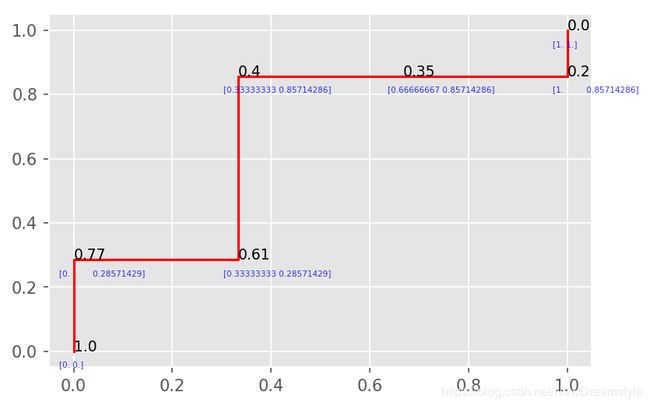
for i,threeshold in enumerate(threesholds):
    plt.text(ROC[i,0],ROC[i,1],threeshold, fontsize=9,)
    plt.text(ROC[i,0]-0.03,ROC[i,1]-0.05,ROC[i], fontsize=5,color = 'b',alpha = 0.8)
plt.plot(ROC[:,0],ROC[:,1],color='red')
plt.show()

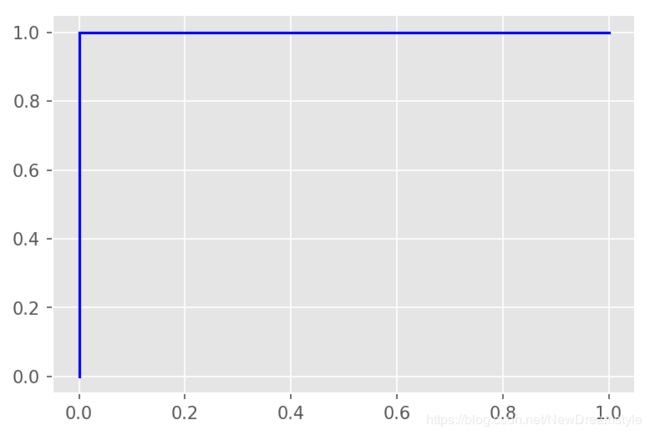
AUC就是对ROC曲线求积分，意为曲下面积，一般取值为(0.5,1) 越大表示模型性能越好
AUC == 1(理想模型)，ROC曲线为

下一篇再写写混淆矩阵 ，召回率和查准率