CART树用于回归应用（python实现）

一、CART ( Classification And Regression Tree) 分类回归树

1、基尼指数：

在分类问题中，假设有KK 个类，样本点属于第kk 类的概率为PkPk ，则概率分布的基尼指数定义为：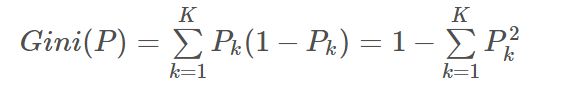 

在CART 分类问题中，基尼指数作为特征选择的依据：选择基尼指数最小的特征及切分点做为最优特征和最优切分点。

2、在回归问题中，特征选择及最佳划分特征值的依据是：划分后样本的均方差之和最小！

二、算法分析：

CART 主要包括特征选择、回归树的生成、剪枝三部分

数据特征停止划分的条件： 
1、当前数据集中的标签相同，返回当前的标签 
2、划分前后的总方差差距很小，数据不划分，返回的属性为空，返回的最佳划分值为当前所有标签的均值。 
3、划分后的左右两个数据集的样本数量较小，返回的属性为空，返回的最佳划分值为当前所有标签的均值。

若满足上述三个特征停止划分的条件，则返回的最佳特征为空，返回的最佳划分特征值会作为叶子结点。

注：CART是一棵二叉树。 在生成CART回归树过程中，一个特征可能会被使用不止一次，所以，不存在当前属性集为空的情况；

1、特征选择（依据：总方差最小）

输入：数据集、op = [m,n] 
输出：最佳特征、最佳划分特征值

m表示剪枝前总方差与剪枝后总方差差值的最小值； n: 数据集划分为左右两个子数据集后，子数据集中的样本的最少数量；

1、判断数据集中所有的样本标签是否相同，是：返回当前标签； 
2、遍历所有的样本特征，遍历每一个特征的特征值。计算出每一个特征值下的数据总方差，找出使总方差最小的特征、特征值 
3、比较划分前和划分后的总方差大小；若划分后总方差减少较小，则返回的最佳特征为空，返回的最佳划分特征值会为当前数据集标签的平均值。 
4、比较划分后的左右分支数据集样本中的数量，若某一分支数据集中样本少于指定数量op[1]，则返回的最佳特征为空， 
返回的最佳划分特征值会为当前数据集标签的平均值。 
5、否则，返回使总方差最小的特征、特征值

二、回归树的生成函数 createTree 
输入：数据集 
输出：生成回归树 
1、得到当前数据集的最佳划分特征、最佳划分特征值 
2、若返回的最佳特征为空，则返回最佳划分特征值（作为叶子节点） 
3、声明一个字典，用于保存当前的最佳划分特征、最佳划分特征值 
4、执行二元切分；根据最佳划分特征、最佳划分特征值，将当前的数据划分为两部分 
5、在左子树中调用createTree 函数, 在右子树调用createTree 函数。 
6、返回树。

注：在生成的回归树模型中，划分特征、特征值、左节点、右节点均有相应的关键词对应。

三、（后）剪枝：（CART 树一定是二叉树，所以，如果发生剪枝，肯定是将两个叶子节点合并）

输入：树、测试集 
输出：树

1、判断测试集是否为空，是：对树进行塌陷处理 
2、判断树的左右分支是否为树结构，是：根据树当前的特征值、划分值将测试集分为Lset、Rset两个集合； 
3、判断树的左分支是否是树结构：是：在该子集递归调用剪枝过程； 
4、判断树的右分支是否是树结构：是：在该子集递归调用剪枝过程； 
5、判断当前树结构的两个节点是否为叶子节点： 
是: 
a、根据当前树结构，测试集划分为Lset,Rset两部分； 
b、计算没有合并时的总方差NoMergeError，即：测试集在Lset 和 Rset 的总方差之和； 
c、合并后，取叶子节点值为原左右叶子结点的均值。求取测试集在该节点处的总方差MergeError，； 
d、比较合并前后总方差的大小；若NoMergeError > MergeError,返回合并后的节点；否则，返回原来的树结构； 
否： 
返回树结构。
 

 

代码：

#-*- coding:utf-8 -*-
from numpy import *
import numpy as np
# 三大步骤：
'''
1、特征的选择：标准：总方差最小
2、回归树的生成：停止划分的标准
3、剪枝：
'''

# 导入数据集
def loadData(filaName):
    dataSet = []
    fr = open(filaName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        theLine = map(float, curLine)                 # map all elements to float()
        dataSet.append(theLine)
    return dataSet

# 特征选择：输入：       输出：最佳特征、最佳划分值
'''
1、选择标准
遍历所有的特征Fi：遍历每个特征的所有特征值Zi；找到Zi,划分后总的方差最小
停止划分的条件：
1、当前数据集中的标签相同，返回当前的标签
2、划分前后的总方差差距很小，数据不划分，返回的属性为空，返回的最佳划分值为当前所有标签的均值。
3、划分后的左右两个数据集的样本数量较小，返回的属性为空，返回的最佳划分值为当前所有标签的均值。
当划分的数据集满足上述条件之一，返回的最佳划分值作为叶子节点；
当划分后的数据集不满足上述要求时，找到最佳划分的属性，及最佳划分特征值
'''

# 计算总的方差
def GetAllVar(dataSet):
    return var(dataSet[:,-1])*shape(dataSet)[0]

# 根据给定的特征、特征值划分数据集
def dataSplit(dataSet,feature,featNumber):
    dataL =  dataSet[nonzero(dataSet[:,feature] > featNumber)[0],:]
    dataR = dataSet[nonzero(dataSet[:,feature] <= featNumber)[0],:]
    return dataL,dataR

# 特征划分
def choseBestFeature(dataSet,op = [1,4]):          # 三个停止条件可否当作是三个预剪枝操作
    if len(set(dataSet[:,-1].T.tolist()[0]))==1:     # 停止条件 1
        regLeaf = mean(dataSet[:,-1])         
        return None, regLeaf                   # 返回标签的均值作为叶子节点
    Serror = GetAllVar(dataSet)
    BestFeature = -1; BestNumber = 0; lowError = inf
    m,n = shape(dataSet)  # m 个样本， n -1 个特征
    for i in range(n-1):    # 遍历每一个特征值
        for j in set(dataSet[:,i].T.tolist()[0]):
            dataL,dataR = dataSplit(dataSet,i,j)
            if shape(dataR)[0] errorMerge:
            print"the leaf merge"
            return leafMean
        else:
            return Tree
    else:
        return Tree

# 预测
def forecastSample(Tree,testData):
    if not isTree(Tree): return float(tree)
    # print"选择的特征是：" ,Tree['spInd']
    # print"测试数据的特征值是：" ,testData[Tree['spInd']]
    if testData[0,Tree['spInd']]>Tree['spVal']:
        if isTree(Tree['left']):
            return forecastSample(Tree['left'],testData)
        else:
            return float(Tree['left'])
    else:
        if isTree(Tree['right']):
            return forecastSample(Tree['right'],testData)
        else:
            return float(Tree['right'])

def TreeForecast(Tree,testData):
    m = shape(testData)[0]
    y_hat = mat(zeros((m,1)))
    for i in range(m):
        y_hat[i,0] = forecastSample(Tree,testData[i])
    return y_hat

if __name__=="__main__":
    print "hello world"
    dataMat = loadData("ex2.txt")
    dataMat = mat(dataMat)
    op = [1, 6]    # 参数1：剪枝前总方差与剪枝后总方差差值的最小值；参数2：将数据集划分为两个子数据集后，子数据集中的样本的最少数量；
    theCreateTree = createTree(dataMat, op)
   # 测试数据
    dataMat2 = loadData("ex2.txt")
    dataMat2 = mat(dataMat2)
    # thePruneTree = pruneTree(theCreateTree, dataMat2)
    #print"剪枝后的后树：\n",thePruneTree
    y = dataMat2[:, -1]
    y_hat = TreeForecast(theCreateTree,dataMat2)
    # y_hat = TreeForecast(thePruneTree,dataMat2)
    print corrcoef(y_hat,y,rowvar=0)[0,1]              # 用预测值与真实值计算相关系数

 

数据集如下：

0.228628	-2.266273
0.965969	112.386764
0.342761	-31.584855
0.901444	87.300625
0.585413	125.295113
0.334900	18.976650
0.769043	64.041941
0.297107	-1.798377
0.901421	100.133819
0.176523	0.946348
0.710234	108.553919
0.981980	86.399637
0.085873	-10.137104
0.537834	90.995536
0.806158	62.877698
0.708890	135.416767
0.787755	118.642009
0.463241	17.171057
0.300318	-18.051318
0.815215	118.319942
0.139880	7.336784
0.068373	-15.160836
0.457563	-34.044555
0.665652	105.547997
0.084661	-24.132226
0.954711	100.935789
0.953902	130.926480
0.487381	27.729263
0.759504	81.106762
0.454312	-20.360067
0.295993	-14.988279
0.156067	7.557349
0.428582	15.224266
0.847219	76.240984
0.499171	11.924204
0.203993	-22.379119
0.548539	83.114502
0.790312	110.159730
0.937766	119.949824
0.218321	1.410768
0.223200	15.501642
0.896683	107.001620
0.582311	82.589328
0.698920	92.470636
0.823848	59.342323
0.385021	24.816941
0.061219	6.695567
0.841547	115.669032
0.763328	115.199195
0.934853	115.753994
0.222271	-9.255852
0.217214	-3.958752
0.706961	106.180427
0.888426	94.896354
0.549814	137.267576
0.107960	-1.293195
0.085111	37.820659
0.388789	21.578007
0.467383	-9.712925
0.623909	87.181863
0.373501	-8.228297
0.513332	101.075609
0.350725	-40.086564
0.716211	103.345308
0.731636	73.912028
0.273863	-9.457556
0.211633	-8.332207
0.944221	100.120253
0.053764	-13.731698
0.126833	22.891675
0.952833	100.649591
0.391609	3.001104
0.560301	82.903945
0.124723	-1.402796
0.465680	-23.777531
0.699873	115.586605
0.164134	-27.405211
0.455761	9.841938
0.508542	96.403373
0.138619	-29.087463
0.335182	2.768225
0.908629	118.513475
0.546601	96.319043
0.378965	13.583555
0.968621	98.648346
0.637999	91.656617
0.350065	-1.319852
0.632691	93.645293
0.936524	65.548418
0.310956	-49.939516
0.437652	19.745224
0.166765	-14.740059
0.571214	114.872056
0.952377	73.520802
0.665329	121.980607
0.258070	-20.425137
0.912161	85.005351
0.777582	100.838446
0.642707	82.500766
0.885676	108.045948
0.080061	2.229873
0.039914	11.220099
0.958512	135.837013
0.377383	5.241196
0.661073	115.687524
0.454375	3.043912
0.412516	-26.419289
0.854970	89.209930
0.698472	120.521925
0.465561	30.051931
0.328890	39.783113
0.309133	8.814725
0.418943	44.161493
0.553797	120.857321
0.799873	91.368473
0.811363	112.981216
0.785574	107.024467
0.949198	105.752508
0.666452	120.014736
0.652462	112.715799
0.290749	-14.391613
0.508548	93.292829
0.680486	110.367074
0.356790	-19.526539
0.199903	-3.372472
0.264926	5.280579
0.166431	-6.512506
0.370042	-32.124495
0.628061	117.628346
0.228473	19.425158
0.044737	3.855393
0.193282	18.208423
0.519150	116.176162
0.351478	-0.461116
0.872199	111.552716
0.115150	13.795828
0.324274	-13.189243
0.446196	-5.108172
0.613004	168.180746
0.533511	129.766743
0.740859	93.773929
0.667851	92.449664
0.900699	109.188248
0.599142	130.378529
0.232802	1.222318
0.838587	134.089674
0.284794	35.623746
0.130626	-39.524461
0.642373	140.613941
0.786865	100.598825
0.403228	-1.729244
0.883615	95.348184
0.910975	106.814667
0.819722	70.054508
0.798198	76.853728
0.606417	93.521396
0.108801	-16.106164
0.318309	-27.605424
0.856421	107.166848
0.842940	95.893131
0.618868	76.917665
0.531944	124.795495
0.028546	-8.377094
0.915263	96.717610
0.925782	92.074619
0.624827	105.970743
0.331364	-1.290825
0.341700	-23.547711
0.342155	-16.930416
0.729397	110.902830
0.640515	82.713621
0.228751	-30.812912
0.948822	69.318649
0.706390	105.062147
0.079632	29.420068
0.451087	-28.724685
0.833026	76.723835
0.589806	98.674874
0.426711	-21.594268
0.872883	95.887712
0.866451	94.402102
0.960398	123.559747
0.483803	5.224234
0.811602	99.841379
0.757527	63.549854
0.569327	108.435392
0.841625	60.552308
0.264639	2.557923
0.202161	-1.983889
0.055862	-3.131497
0.543843	98.362010
0.689099	112.378209
0.956951	82.016541
0.382037	-29.007783
0.131833	22.478291
0.156273	0.225886
0.000256	9.668106
0.892999	82.436686
0.206207	-12.619036
0.487537	5.149336

运行结果：

只进行前剪枝：

进行前、后 两次剪枝：

 

注：

• 由于.txt文档中给出的数据集，y = f(x) 的回归问题中，x只有一个维度，因此在维度选择时只有一次，比较特殊
• 因此导致了，在进行前、后剪枝操作后，求得的“相关系数”与只进行前剪枝操作后的“相关系数”相等。而一般情况下是进行两次剪枝后，回归树的性能更好

 

参考资料：

https://blog.csdn.net/qq_32933503/article/details/78408259#commentsedit