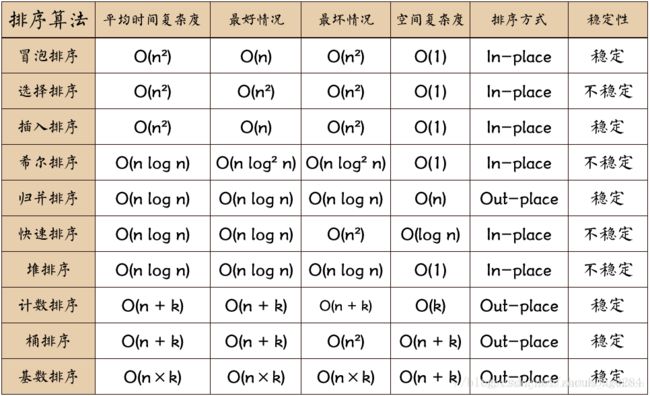
在编程中比较常用的几种排序

在编程中一般有十种而常用排序分别是：冒泡排序，选择排序，插入排序，希尔排序，归并排序，快速排序。

不常用排序有：堆排序，计数排序，桶排序，基数排序

冒泡排序

冒泡排序（英语：Bubble Sort）是⼀种简单的排序算法。它重复地遍历要排序的数列，⼀次⽐较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的⼯作是重复地进⾏直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越⼩的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下：

• ⽐较相邻的元素。如果第⼀个⽐第⼆个⼤（升序），就交换他们两个。
• 对每⼀对相邻元素作同样的⼯作，从开始第⼀对到结尾的最后⼀对。
• 这步做完后，最后的元素会是最⼤的数。针对所有的元素重复以上的步骤，除了最后⼀个。
• 持续每次对越来越少的元素重复上⾯的步骤，直到没有任何⼀对数字需要⽐较。

程序

a=[2,3,4,5,0,1,6,7,9,8]
def sort ():
    """冒泡排序"""
    n=len(a)
    for i in range (n-1,0,-1):
        for j in range (i):
            if a[j]>a[j+1]:
                a[j],a[j+1]=a[j+1],a[j]
if __name__ == '__main__':
    sort()
    print(a)	

选择排序

选择排序（Selection sort）是⼀种简单直观的排序算法。它的⼯作原理如下。⾸先在未排序序列中找到最⼩（⼤）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最（⼤）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

程序

a=[2,3,4,5,0,1,6,7,9,8]
def sort():
	"""选择排序 """
    n = len(a)
 	#需要进⾏n-1次选择操作
    for i in range(n-1):# 记录最⼩位置
        min_index = i
 		#从i+1位置到末尾选择出最⼩数据
        for j in range(i+1, n):
            if a[j] < a[min_index]:
                min_index = j
		# 如果选择出的数据不在正确位置，进⾏交换
        if min_index != i:
            a[i], a[min_index] = a[min_index], a[i]
if __name__ == '__main__':
    sort()
    print(a)

插入排序

插⼊排序（英语：Insertion Sort）是⼀种简单直观的排序算法。它的⼯作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插⼊。插⼊排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插⼊空。

程序

a=[2,3,4,5,0,1,6,7,9,8]
def sort():
    """插入排序"""
    n=len(a)
    #从第二个位置，即下标为1的元素开始向前插入
    for i in range (1,n):
        #从第i个元素开始向前比较，如果小于前一个元素交换元素
        for j in range (i,0,-1):
            if a[j] < a[j - 1]:
                a[j], a[j - 1] = a[j -1], a[j]
if __name__ == '__main__':
    sort()
    print(a）

希尔排序

希尔排序(Shell Sort)是插⼊排序的⼀种。也称缩⼩增量排序，是直接插⼊排序算法的⼀种更⾼效的改进版本。希尔排序是⾮稳定排序算法。该⽅法因DL．Shell于1959年提出⽽得名。 希尔排序是把记录按下标的⼀定增量分组，对每组使⽤直接插⼊排序算法排序；随着增量逐渐减少，每组包含的关
键词越来越多，当增量减⾄1时，整个⽂件恰被分成⼀组，算法便终⽌。

程序

  a = [2, 3, 4, 5, 0, 1, 6, 7, 9, 8]
def sort():
    """希尔排序"""
    n=len(a)
    gap=n//2
    while gap>0:
        #按步长进行插入排序
        for i in range (gap,n):
            j =i
            while j>=gap and a[j-gap]>a[j]:
                a[j-gap],a[j]=a[j],a[j-gap]
                j-=gap
        #得到新的步长
        gap=gap//2
if __name__ == '__main__':
    sort()
    print(a)  

归并排序

归并排序是采⽤分治法的⼀个⾮常典型的应⽤。归并排序的思想就是先递归分解数组，再合并数组。将数组分解最⼩之后，然后合并两个有序数组，基本思路是⽐较两个数组的最前⾯的数，谁⼩就先取谁，取了后相应的指针就往后移⼀位。然后再⽐较，直⾄⼀个数组为空，最后把另⼀个数组的剩余部分复制过来即可。

程序

a=[2,3,4,5,0,1,6,7,9,8]
def merge_sort(a):
    if len(a) <= 1:
        return a
    # ⼆分分解
    num = len(a)//2
    left = merge_sort(a[:num])
    right = merge_sort(a[num:])
    # 合并
    return merge(left,right)#递归调用
def merge(left, right):
    """合并操作，将两个有序数组left[]和right[]合并成⼀个⼤的有序数组'"""
    """归并排序"""
#left与right的下标指针
    l, r = 0, 0
    result = []
    while l

快速排序

快速排序（英语：Quicksort），⼜称划分交换排序（partition-exchangesort），通过⼀趟排序将要排序的数据分割成独⽴的两部分，其中⼀部分的所有数据都⽐另外⼀部分的所有数据都要⼩，然后再按此⽅法对这两部分数据分别进⾏快速排序，整个排序过程可以递归进⾏，以此达到整个数据变成
有序序列。
步骤为：

1. 从数列中挑出⼀个元素，称为"基准"（pivot），
2. 重新排序数列，所有元素⽐基准值⼩的摆放在基准前⾯，所有元素⽐基准值⼤的摆在基准的后⾯（相同的数可以到任⼀边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把⼩于基准值元素的⼦数列和⼤于基准值元素的子数列排序。
4. 递归的最底部情形，是数列的⼤⼩是零或⼀，也就是永远都已经被排序好了。虽然⼀直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它⾄少会把⼀个元素摆到它最后的位置去。

程序

a=[2,3,4,5,0,1,6,7,9,8]
	def sort (a,start,end):
	    """快速排序"""
	    if start>=end:#递归的退出条件
	        return
	    mid=a[start]#设定起始元素
	    low=start#low为序列左边的由左向右移动的游标
	    high=end# high为序列右边的由右向左移动的游标
	    while low =mid:
	            high -= 1
	        a[low]=a[high]# 将high指向的元素放到low的位置上
	        # 如果low与high未重合，low指向的元素⽐基准元素⼩，则low向右
	        while low

排序的稳定性和复杂性