最短路径算法之Dijkstra算法
基本思想
通过Dijstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始),引进两个集合S和U。S的作用是记录已求出最短路径的顶点 (以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点。初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。重复改操作,直到遍历完所有顶点。
步骤
(1)初始时,S中只包含起点s;U中包含出s外的其他顶点,且U中顶点的距离为"起点到该顶点的距离"。
(2)从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3)更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出的最短路径的顶点,从而可以利用k来更新其他顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4)重复步骤(2)和(3),直到遍历完所有顶点。
实例讲解
以图G4为例,下面进行Dijkstra的算法步骤。
首先我们以图中D为起点为例。
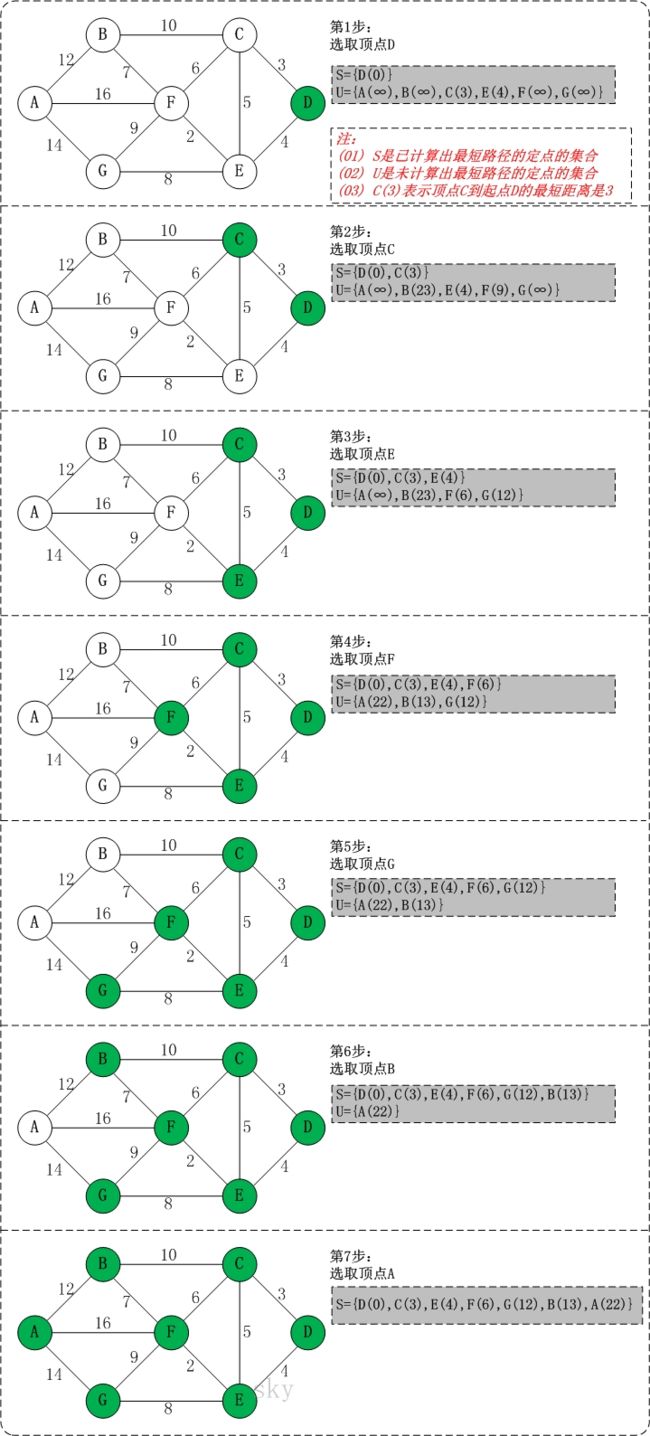
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
算法实现
public class Dijkstra {
private static int N = 1000;
private static int[][] Graph = {
{ 0, 1, 5, N, N, N, N, N, N },
{ 1, 0, 3, 7, 5, N, N, N, N },
{ 5, 3, 0, N, 1, 7, N, N, N },
{ N, 7, N, 0, 2, N, 3, N, N },
{ N, 5, 1, 2, 0, 3, 6, 9, N },
{ N, N, 7, N, 3, 0, N, 5, N },
{ N, N, N, 3, 6, N, 0, 2, 7 },
{ N, N, N, N, 9, 5, 2, 0, 4 },
{ N, N, N, N, N, N, 7, 4, 0 } };
public static void main(String[] args) {
dijkstra(0, Graph);
}
/**
* Dijkstra最短路径。
* 即图中"节点vs"到其它各个节点的最短路径。
* @param vs 起始节点
* @param Graph 图
*/
public static void dijkstra(int vs, int[][] Graph) {
int NUM = Graph[0].length;
// 前驱节点数组
int[] prenode = new int[NUM];
// 最短距离数组
int[] mindist = new int[NUM];
// 该节点是否已经找到最短路径
boolean[] find = new boolean[NUM];
int vnear = 0;
for (int i = 0; i < mindist.length; i++) {
prenode[i] = i;
mindist[i] = Graph[vs][i];
find[i] = false;
}
find[vs] = true;
for (int v = 1; v < Graph.length; v++) {
// 每次循环求得距离vs最近的节点vnear和最短距离min
int min = N;
for (int j = 0; j < Graph.length; j++) {
if (!find[j] && mindist[j] < min) {
min = mindist[j];
vnear = j;
}
}
find[vnear] = true;
// 根据vnear修正vs到其他所有节点的前驱节点及距离
for (int k = 0; k < Graph.length; k++) {
if (!find[k] && (min + Graph[vnear][k]) < mindist[k]) {
prenode[k] = vnear;
mindist[k] = min + Graph[vnear][k];
}
}
}
for (int i = 0; i < NUM; i++) {
System.out.println("v" + vs + "...v" + prenode[i] + "->v" + i + ", s=" + mindist[i]);
}
}
}