Java版高级数据结构算法 - 红黑树

知识的学习在于点滴记录，坚持不懈；知识的学习要有深度和广度，不能只流于表面，坐井观天；知识要善于总结，不仅能够理解，更知道如何表达！

红黑树的定义

AVL树为了维护节点平衡，在插入和删除时做了大量的旋转操作，当数据量大了以后，AVL树的旋转操作就拖慢了插入删除的时间，那么红黑树相比于AVL树，插入删除的旋转次数要少了很多，那是因为红黑树并不是一颗绝对平衡的树，它的节点左右子树的高度差不超过2倍（长不超过短的2倍）。

红黑树的性质定义：
1.每一节点都有颜色，不是黑色就是红色
2.根节点root是黑色的
3.叶子节点都是黑色（指叶子节点的地址域null为黑色，一般null节点默认颜色是黑色）
4.不能出现连续的红色节点，也就是说红色节点的孩子节点必须是黑色的
5.从根节点到每一个叶子节点的路径上，黑色节点的数量是一样多的

在进行红黑树的插入删除操作的时候，会涉及节点的旋转和重新着色问题，红黑树的旋转次数要比AVL少很多，插入最多旋转两次，删除最多旋转三次。

像Java的TreeMap，TreeSet，C++的set和map容器，Linux的虚拟内存管理，epoll的内核层实现都应用到了红黑树这种数据结构，其增删查时间复杂度能达到$O(lo{g}_{2}n)$。

下面给出红黑树的基本定义：

/**
 * 红黑树节点颜色定义
 */
enum COLOR{
    BLACK,
    RED
}

/**
 * 红黑树节点类型定义
 * @param 
 */
class RBNode<T extends Comparable<T>>{
    private T data;
    private RBNode<T> left;
    private RBNode<T> right;
    private RBNode<T> parent;
    private COLOR color;

    public RBNode(T data, COLOR color) {
        this.data = data;
        this.color = color;
        this.left = this.right = this.parent = null;
    }

    public RBNode(T data, COLOR color, RBNode<T> parent, RBNode<T> left, RBNode<T> right) {
        this.data = data;
        this.left = left;
        this.right = right;
        this.parent = parent;
        this.color = color;
    }

    public T getData() {
        return data;
    }

    public void setData(T data) {
        this.data = data;
    }

    public RBNode<T> getLeft() {
        return left;
    }

    public void setLeft(RBNode<T> left) {
        this.left = left;
    }

    public RBNode<T> getRight() {
        return right;
    }

    public void setRight(RBNode<T> right) {
        this.right = right;
    }

    public RBNode<T> getParent() {
        return parent;
    }

    public void setParent(RBNode<T> parent) {
        this.parent = parent;
    }

    public COLOR getColor() {
        return color;
    }

    public void setColor(COLOR color) {
        this.color = color;
    }
}

/**
 * 红黑树定义
 * @param 
 */
class RBTree<T extends Comparable<T>>{
    private RBNode<T> root;

    /**
     * 获取红黑树节点颜色
     * @param node
     * @return
     */
    private COLOR color(RBNode<T> node){
        return node == null ? COLOR.BLACK : node.getColor();
    }
    
    /**
     * 设置节点颜色
     * @param node
     * @param color
     */
    private void setColor(RBNode<T> node, Color color){
        node.setColor(color);
    }

    /**
     * 获取当前节点的父节点
     * @param node
     * @return
     */
    private RBNode<T> parent(RBNode<T> node){
        return node.getParent();
    }

    /**
     * 获取node节点的左孩子节点
     * @param node
     * @return
     */
    private RBNode<T> left(RBNode<T> node){
        return node.getLeft();
    }

    /**
     * 获取node节点的右孩子节点
     * @param node
     * @return
     */
    private RBNode<T> right(RBNode<T> node){
        return node.getRight();
    }
}

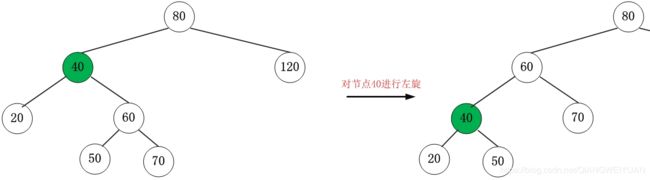
红黑树的左旋和右旋

红黑树的旋转操作比AVL少，主要分为左旋和右旋操作，由于红黑树在调整节点颜色的时候，需要经常访问父节点，祖先节点，叔叔节点，兄弟节点，因此每一个节点都记录了它的parent，用于从当前节点向上访问节点，如下：

红黑树的左旋代码：

/**
 * 红黑树节点的左旋转操作
 * @param node
 * @return
 */
private void leftRotate(RBNode<T> node){
    RBNode<T> child = node.getRight();
    child.setParent(node.getParent());
    if(node.getParent() == null)
        this.root = child;
    else if(node.getParent().getLeft() == node)
        node.getParent().setLeft(child);
    else
        node.getParent().setRight(child);
    node.setParent(child);
    node.setRight(child.getLeft());
    if(child.getLeft() != null)
        child.getLeft().setParent(node);
    child.setLeft(node);
}

红黑树的右旋代码：

/**
 * 红黑树节点的右旋转操作
 * @param node
 * @return
 */
private void rightRotate(RBNode<T> node){
    RBNode<T> child = node.getLeft();
    child.setParent(node.getParent());
    if(node.getParent() == null)
        this.root = child;
    else if(node.getParent().getLeft() == node)
        node.getParent().setLeft(child);
    else
        node.getParent().setRight(child);
    node.setParent(child);
    node.setLeft(child.getRight());
    if(child.getRight() != null)
        child.getRight().setParent(node);
    child.setRight(node);
}

红黑树的插入操作

红黑树的根节点是黑色，其它新插入的节点都是红色节点，因为红色节点不影响红黑树的性质，不会影响某一个路径上黑色节点的数量，如果新插入的红色节点，其父节点是黑色的，那么插入直接结束；但是如果新插入的红色节点的父节点也是红色的，那么就不满足红黑树的性质了，需要进行调整。

红黑树的节点插入过程和BST树一样，只不过插入节点以后，要进行一个判断是否调整的过程，其主要分为三种情况：

1.叔叔节点如果也是红色，把父节点和叔叔节点都设置成黑色，把祖父节点设置成红色，然后从祖父节点开始继续向上回溯

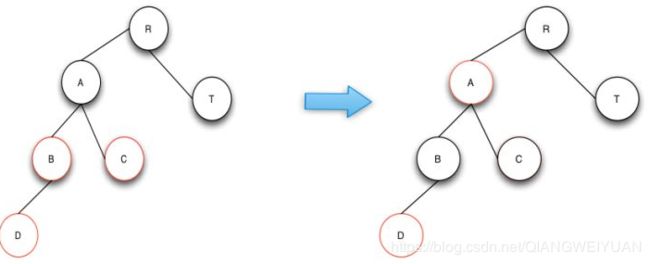
2.叔叔节点是黑色，当前节点和父节点，祖父节点在一条线上，直接进行一个旋转操作，把父节点设置成黑色，祖父节点都设置成红色，相当于把父节点和祖父节点的颜色进行交换

3.叔叔节点是黑色，当前节点和父节点，祖父节点不在一条线上，要进行两次旋转操作

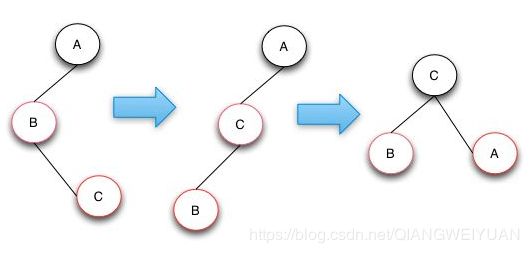
通过上面的三种情况的判断处理，才能继续保持红黑树的性质不被破坏，代码示例：

/**
 * 红黑树插入操作
 * @param val
 */
public void insert(T val){
    if(root == null){
        root = new RBNode<>(val, COLOR.BLACK);
        return;
    }

    RBNode<T> parent = null;
    RBNode<T> cur = root;
    while(cur != null){
        if(cur.getData().compareTo(val) > 0){
            parent = cur;
            cur = cur.getLeft();
        } else if(cur.getData().compareTo(val) < 0){
            parent = cur;
            cur = cur.getRight();
        } else {
            return;
        }
    }

    RBNode<T> node = new RBNode<T>(val, COLOR.RED, parent, null, null);
    if(parent.getData().compareTo(node.getData()) > 0){
        parent.setLeft(node);
    } else{
        parent.setRight(node);
    }

    // 如果新插入节点的父节点是红色，则进行红黑树的插入调整
    if(color(parent) == COLOR.RED){
        fixAfterInsert(node);
    }
}

/**
 * 红黑树插入调整函数
 * @param node
 */
private void fixAfterInsert(RBNode<T> node) {

    // node节点的父节点是红色，出现连续的红色节点，需要调整颜色
    while(color(parent(node)) == COLOR.RED){
        // 插入节点在祖父节点的左子树上
        if(left(parent(parent(node))) == parent(node)){
            // 叔叔节点是红色
            RBNode<T> uncle = right(parent(parent(node)));
            if(color(uncle) == COLOR.RED){
                setColor(parent(node), COLOR.BLACK);// 父节点置黑色
                setColor(uncle, COLOR.BLACK); //叔叔节点置黑色
                setColor(parent(parent(node)), COLOR.RED); // 祖父节点置红色
                node = parent(parent(node)); // node指向祖父节点，继续向上回溯调整
            } else {
                // 叔叔节点是黑色，祖父，父亲，当前节点不在一条直线上
                if(right(parent(node)) == node){
                    // 做一个左旋转操作
                    node = parent(node);
                    leftRotate(node);
                }

                // 祖父，父亲，当前节点在一条直线上，直接做右旋转操作
                setColor(parent(node), COLOR.BLACK);// 父节点设置成黑色，旋转以后就成为根节点了
                setColor(parent(parent(node)), COLOR.RED);// 祖父节点设置成红色
                // 以祖父节点为根节点做一个右旋转操作
                rightRotate(parent(parent(node)));
                break; // 调整完成，跳出循环
            }
        } else {
            // 插入节点在祖父节点的右子树上，和上面的所有情况刚好相反
            RBNode<T> uncle = left(parent(parent(node)));
            if(color(uncle) == COLOR.RED){
                setColor(parent(node), COLOR.BLACK);
                setColor(uncle, COLOR.BLACK);
                setColor(parent(parent(node)), COLOR.RED);
                node = parent(parent(node));
            } else {
                if(left(parent(node)) == node){
                    node = parent(node);
                    rightRotate(node);
                }

                setColor(parent(node), COLOR.BLACK);
                setColor(parent(parent(node)), COLOR.RED);
                leftRotate(parent(parent(node)));
                break; // 调整完成，跳出循环
            }
        }
    }

    // 有可能回溯时把根节点置成红色，直接把根节点设置成黑色
    setColor(this.root, Color.BLACK);
}

红黑树的删除操作

红黑树的删除操作比插入操作要复杂一点，如果删除的是红色节点，直接删除就可以；如果删除的是黑色节点，删除完节点需要进行调整，因为破坏了红黑树的性质，某一个分支路径上的黑色节点少了一个。删除主要分为四种情况：

1.兄弟节点是红色，无法借调一个黑色节点过来，但是兄弟节点的孩子节点肯定都是黑色的，旋转以后，把黑色的兄弟节点提上来，就可以借调黑色节点了。

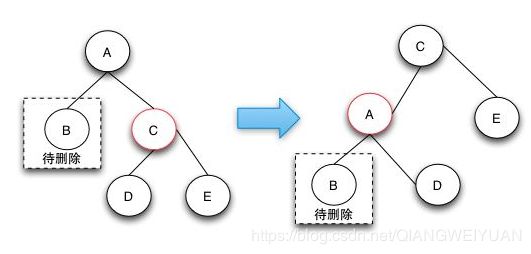
2.兄弟节点是黑色的，而且兄弟节点的两个孩子也都是黑色的，直接把兄弟节点设置成红色，然后从父节点开始继续回溯调整。

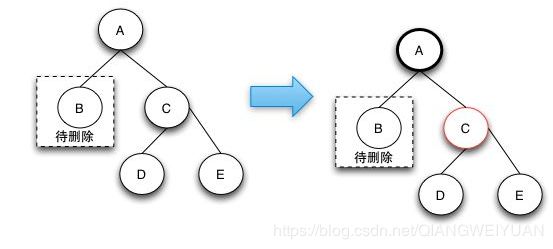
3.兄弟节点是黑色，而且兄弟节点的左孩子是红色的，右孩子是黑色的（兄弟节点在右边），如果兄弟节点在左边的话，就是兄弟节点的右孩子是红色的，左孩子是黑色的，进行一次旋转操作。

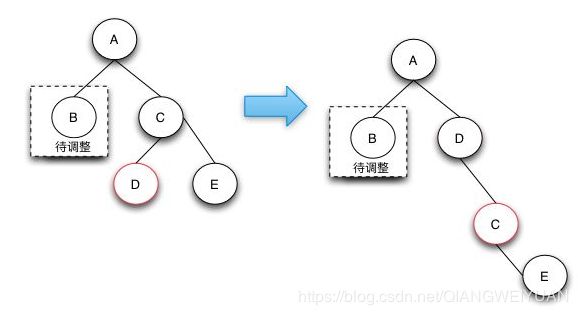
4.兄弟节点是黑色，右孩子是红色的（兄弟节点在右边），如果兄弟节点在左边的话，就是兄弟节点的左孩子是红色的，进行一次旋转操作结束。

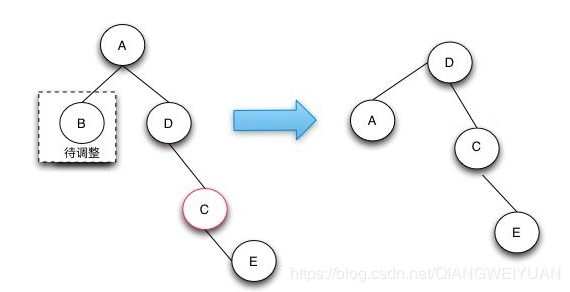
红黑树的删除代码如下：

/**
 * 红黑树删除操作
 * @param val
 */
public void remove(T val){
    if(this.root == null){
        return;
    }

    RBNode<T> cur = this.root;
    while(cur != null){
        if(cur.getData().compareTo(val) > 0){
            cur = cur.getLeft();
        } else if(cur.getData().compareTo(val) < 0){
            cur = cur.getRight();
        } else {
            break;
        }
    }

    if(cur == null){
        return;
    }

    // 情况3 待删除节点有两个孩子 转换成 有一个孩子的节点，或者叶子节点的删除
    if(cur.getLeft() != null && cur.getRight() != null){
        // 用后继节点代替
        RBNode<T> old = cur;
        cur = cur.getRight();
        while(cur.getLeft() != null){
            cur = cur.getLeft();
        }
        old.setData(cur.getData());
    }

    // 处理情况1，2  删除节点没有孩子或者有一个孩子
    RBNode<T> child = (cur.getLeft() != null ? cur.getLeft() : cur.getRight());
    if(child != null){
        child.setParent(cur.getParent());
        if(cur.getParent() == null){
            this.root = child;
        } else if(cur.getParent().getLeft() == cur){
            cur.getParent().setLeft(child);
        } else {
            cur.getParent().setRight(child);
        }

        // 如果删除的是黑色节点，需要进行调整
        if(cur.getColor() == COLOR.BLACK){
            fixAfterDelete(child);
        }
    } else {
        if(cur.getParent() == null){
            this.root = null;
        } else {
            // 删除的是叶子节点
            if(cur.getColor() == COLOR.BLACK){
                fixAfterDelete(cur);
            }

            // 当前删除节点cur没有孩子节点，上面把cur当作虚拟节点，进行红黑树的删除调整，完成后，把cur节点删除掉
            if(cur.getParent().getLeft() == cur){
                cur.getParent().setLeft(null);
            } else {
                cur.getParent().setRight(null);
            }
        }
    }
}

/**
 * 红黑树删除调整函数
 * @param node
 */
private void fixAfterDelete(RBNode<T> node) {
    // 回溯过程中遇到根节点或者红色节点结束循环
    while(node != this.root
            && color(node) == COLOR.BLACK){
        if(node == left(parent(node))){
            RBNode<T> b = right(parent(node));
            // 情况一，兄弟节点是红色，无法借一个黑色节点，需要左旋转，把兄弟节点的子节点黑色节点往上提
            if(color(b) == COLOR.RED){
                b.setColor(COLOR.BLACK);
                parent(node).setColor(COLOR.RED);
                leftRotate(parent(node));
                b = right(parent(node));
            }

            // 情况二，兄弟节点是黑色，而且兄弟节点的两个孩子也是黑色节点，把兄弟节点改成红色，继续回溯父节点
            if(color(left(b)) == COLOR.BLACK
                    && color(right(b)) == COLOR.BLACK){
                b.setColor(COLOR.RED);
                node = parent(node);
            } else {
                // 情况三，兄弟节点是黑色，但是右孩子没有红色节点（借给左子树后，右子树设法给自己添加一个黑色节点保证黑色节点数量不变）
                if(color(right(b)) == COLOR.BLACK){
                    left(b).setColor(COLOR.BLACK);
                    b.setColor(COLOR.RED);
                    rightRotate(b);
                    b = right(parent(node));
                }

                // 情况四， 兄弟节点是黑色，而且右孩子是红色，直接左旋，并把有孩子直接调成黑色
                b.setColor(parent(node).getColor());
                parent(node).setColor(COLOR.BLACK);
                right(b).setColor(COLOR.BLACK);
                leftRotate(parent(node));
                node = this.root;
            }
        } else {
            RBNode<T> b = left(parent(node));
            // 情况一，兄弟节点是红色，无法借一个黑色节点，需要右旋转，把兄弟节点的子节点黑色节点往上提
            if(color(b) == COLOR.RED){
                b.setColor(COLOR.BLACK);
                parent(node).setColor(COLOR.RED);
                rightRotate(parent(node));
                b = left(parent(node));
            }

            // 情况二，兄弟节点是黑色，而且兄弟节点的两个孩子也是黑色节点
            if(color(left(b)) == COLOR.BLACK
                    && color(right(b)) == COLOR.BLACK){
                b.setColor(COLOR.RED);
                node = parent(b);
            } else {
                // 情况三，兄弟节点是黑色，但是左孩子没有红色节点
                if(color(left(b)) == COLOR.BLACK){
                    right(b).setColor(COLOR.BLACK);
                    b.setColor(COLOR.RED);
                    leftRotate(b);
                    b = left(parent(node));
                }

                // 情况四， 兄弟节点是黑色，而且左孩子是红色，直接左旋，并把有孩子直接调成黑色
                b.setColor(parent(node).getColor());
                parent(node).setColor(COLOR.BLACK);
                left(b).setColor(COLOR.BLACK);
                rightRotate(parent(node));
                node = this.root;
            }
        }
    }

    /**
     * 删除黑色节点后，其孩子节点是红色，直接调成黑色，结束上面循环，保持黑色节点数量不变；
     * 删除黑色节点后，其孩子节点是黑色，但是向上回溯的时候，遇到红色节点，直接改成黑色节点，结束上面循环，保持黑色节点数量不变
     */
    node.setColor(COLOR.BLACK);
}