2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛题解

2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛题解

萌新又来写题解啦
原题链接

(不是按照题号顺序来的QWQ）

L. Lottery Tickets
题意：给0-9的卡片若干，要求组成一个数，该数能被4整除且最大。卡片可以不全用上。

tips：能被4整除的数字，末尾两位必可以被4整除。
注意分类讨论（特判）的情况有点多qwq:
A.只有0(区别于B） 输出0
B.有一个0 但是没2468 输出0 （只有13579和0无法组成两位数被4整除）
C.有一个4 但是没0268 输出4
D.有一个8 但是没0246 输出8
E.其他
E1.有多于1个零，且有别的数字，零放最后。（整百可以被4整除）
E2.按照如下顺序输出。
{20,12,32,40,24,44,52,60,16,36,64,56,72,76,80,28,84,48,68,88,92,96};
排序规则：按照最大数字最小，最大数字相同则最小数字最小的顺序排序。（其实就是个贪心）

代码：（写的比较乱，但是就是这几种分类讨论）

#include
using namespace std;

int book[25] = {20,12,32,40,24,44,52,60,16,36,64,56,72,76,80,28,84,48,68,88,92,96};
int card[15],t;

bool judge(int x){
	if(x == 44)		return (card[4] >= 2) ? true : false; 
	if(x == 88)		return (card[8] >= 2) ? true : false; 
	else	return (card[x % 10] >= 1 && card[x / 10] >= 1)	? true : false; 
}

int main(){
	scanf("%d",&t);
	while(t--){
		string s = "";
		for(int i = 0; i <= 9; ++i)
			scanf("%d",&card[i]);
		if(card[0] == 1 && !card[2] && !card[4] && !card[6] && !card[8] && (card[1] || card[3] || card[5] || card[7] || card[9]))	s = "0";//A
		else if(card[0] > 0 && !card[2] && !card[4] && !card[6] && !card[8] && !card[1] && !card[3] && !card[5] && !card[7] && !card[9])	s = "0";		//B
		else if(card[4] == 1 && !card[2] && !card[8] && !card[6] && !card[0])	s = "4";		//C
		else if(card[8] == 1 && !card[2] && !card[4] && !card[6] && !card[0])	s = "8";		//D
		else if(card[0] >= 2 && (card[1] || card[2] || card[3] || card[5] || card[6] || card[7] || card[4] || card[9] || card[8])){		//E1
			s += "00";
			card[0] -= 2;
			for(int i = 0; i <= 9; ++i){
				for(int j = card[i]; j > 0; --j)
					s += i + '0';
			}
			reverse(s.begin(),s.end());
		}else{			//E2
			int idx;
			for(idx = 0; idx < 22; ++idx){
				if(judge(book[idx])){
					s += book[idx] % 10 + '0', card[book[idx] % 10]--;
					s += book[idx] / 10 + '0', card[book[idx] / 10]--;
					break;
				}
			}
			if(idx == 22){
				printf("-1\n");
				continue;
			}	
			for(int i = 0; i <= 9; ++i){
				for(int j = card[i]; j > 0; --j)
					s += i + '0';
			}
			reverse(s.begin(),s.end());
		}
		cout << s << endl;
	}
	return 0;
}

D. Disaster Recovery
题意：n 点 m 边无向联通图，第 i 个点的点权是斐波那契数列第 i
项，边权是两端点点权之和，求原图的一个最小生成树使得度数最
大的点的度数最小。
看图qwq.城市编号是fib数列，权值是两个数相加。问怎么修路，能把城市连通起来！

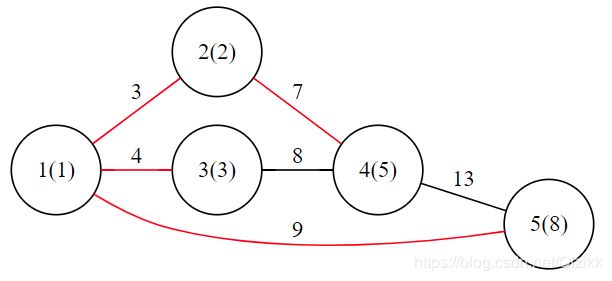
tips:几乎裸kruskal最小生成树。利用fib数列的性质，按照pair排序，可以得到边权从小到大的排列。（pair排序按照从小到大的顺序排序，fib数列，max大的一定大。因为就算另外一个是max-1项,max-2项,也有max-1项+max-2项= max项.)
然后直接算kruskal。

注意用vector写，否则会mle……

#include
using namespace std;
typedef pair<int, int> p;
const int maxn = 200005;
int n,m,cnt,f[100005],degree[100005],ans,x,y;
int find(int x){return f[x] == x ? x : f[x] = find(f[x]);}
int unite(int x, int y){
	int fa = find(x), fb = find(y);
	if(fa == fb)	return 0;
	else	f[fb] = f[fa];
	return 1;
} 
void init(){
	for(int i = 1; i <= n; ++i)	f[i] = i;
	ans = cnt = 0;
}
vector<p> edge;

int cmp(p r1, p r2){
	//return r1.second == r2.second ? r1.first < r2.first : r1.second < r2.second; 一样的写法
	if(r1.second != r2.second)
		return r1.second < r2.second;
	else	return r1.first < r2.first;
}

int main(){
	scanf("%d%d",&n,&m);
	init();
	for(int i = 1; i <= m; ++i){
		scanf("%d%d",&x, &y);
		if (x > y) swap(x, y);
		edge.push_back(make_pair(x, y));
	}
	sort(edge.begin(), edge.end(), cmp);
	for(int i = 0; i < m; ++i){
		int u = edge[i].first, v = edge[i].second;
		if(unite(u,v))
			degree[u]++, degree[v]++;
	}
	int res = 0;
    for (int i = 1; i <= n; i++) res = max(res, degree[i]);
	printf("%d\n",res);
	return 0;
}
 

但是！！这个题有一种看似正确实际错误的贪心！比较值得积累。
“贪心先把1连完 再连2 以此类推，因为某一个点和其他点相连，编号总是越小越好”。代码实现即把上面的cmp函数换一下first/second的位置。
这样会WA!!!
结论是，不能这么贪！！
1-4，1-5，2-3，2-5，3-4
按1-5的顺序贪:1-4,1-5,2-3,2-5
按边权贪：2-3,1-4,3-4,1-5

以上述为例，5在连了1之后已经被连入，不一定要和2直接相连。（可以通过其他点间接到达2号点）。所以贪心是错误的qwqqqq

其次！！ 加深一下kruskal的理解，为什么要用并查集，而不直接使用set.
抛开本题，如果边权按小到大顺序是1-3，2-4，2-3.如果用set，2-3这条边就连不起来了qwq……

D. Disaster Recovery
t题意：生草题。n × m 网格图，每个格子内的草每秒增加 ai,j，接下
来 k 个操作，每个操作会在某个时间把某一列或某一行的草割光，
求最终割掉的草的总和。

tips:每个格子的贡献只取决于它最后一次被割的时间.用标记记录一下即可。注意如果循环每一行/列的格子标记，会TLE.直接对一行/一列作为整体标记，算的时候对于行和列的标记比较大小即可。
注意（a % mod) * ( b % mod) % mod,直接乘会爆。

#include			
#define ll long long 
#define mod 998244353
using namespace std;
int n,m,k,idx;
ll ans,ttime,mp[505][505],lie[505],hang[505],book[505][505];
char c;

int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j)
			scanf("%lld",&mp[i][j]);
	}
	for(int i = 1; i <= k; ++i){
		getchar();
		scanf("%c%d%lld",&c,&idx,&ttime);
		if(c == 'r'){
			for(int i = 1; i <= m; ++i){
				ll tmp = (ttime - max(hang[idx],lie[i]));
				book[idx][i] = (book[idx][i] % mod + tmp % mod) % mod;
			}
			hang[idx] = ttime;
		}else{
			for(int i = 1; i <= n; ++i){
				ll tmp = (ttime - max(lie[idx],hang[i]));
				book[i][idx] = (book[i][idx] % mod + tmp % mod) % mod;
			}
			lie[idx] = ttime;
		}
	}
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j){
			ll tmp = (mp[i][j] % mod * book[i][j] % mod ) % mod;
			ans = (ans % mod + tmp % mod) % mod;
		}
	}
	printf("%lld",ans);
	return 0;
}

A. Archmage
题意：大法师蓝量上限为 n ，每秒可以花费 x 释放一次技能，每秒
会自动回蓝 y 点，后结算回蓝，问 m 秒内能最多放几次技能。
tips:一个公式（见代码）。
A.如果有 x ≤ y, 则他显然每秒都能释放一次技能
B.如果有 x > y, 则前 m - 1 秒内恢复的魔法值都可以被利用上。

#include
#define ll long long
using namespace std;

ll n,m,x,y,t;

int main(){
	scanf("%d",&t);
    while(t--){
        scanf("%lld%lld%lld%lld",&n,&m,&x,&y);
        printf("%lld\n",min(m, (n + (m - 1) * y) / x));
    }
    return 0;
}

B/C略 签到题qwq