动手学深度学习(tensorflow)---学习笔记整理（二、线性回归篇）

（有关公式、基本理论等大量内容摘自《动手学深度学习》(TF2.0版)）

首先说一下线性回归是什么？

个人理解：线性回归利用某种方法来确定两种或两种以上变量间相互依赖的定量关系的一种分析方法。简单点说，现在有一些随机点，通过某种方法找出来他所符合的线性方程。用途嘛～例如，我们有房价和决定因素的相关数据，可以找到它符合的线性函数，然后对房价进行预测～

线性回归的基本要素

简单点说就是自变量们和因变量。用一个例子来说，以一个房屋价格预测为例，这个应用的目标是预测一栋房子的售出价格（元）。我们知道这个价格取决于很多因素，如房屋状况、地段、市场行情等。为了简单起见，这里我们假设价格只取决于房屋状况的两个因素，即面积（平方米）和房龄（年）。接下来我们希望探索价格与这两个因素的具体关系。

模型的定义

模型的训练

模型的训练指通过利用数据来寻找特定的神经网络模型的参数值，使模型在数据上的误差尽可能小。主要有以下三个方面的内容。

（1）训练数据

（2）损失函数

（3）优化算法

模型的预测

为什么学习深度学习要先学习线性回归？

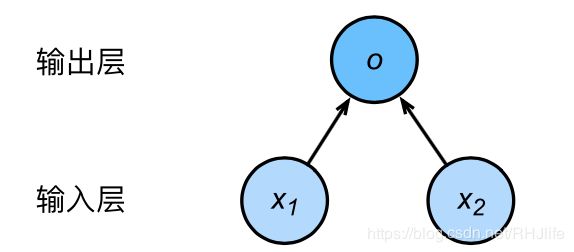
线性回归可以理解成一层的神经网络，是最简单的神经网络，学会线性回归可以更好的学习更深层的网络。以上述房价预测为例的线性回归的神经网络如下图所示：

输入分别为 x1​ 和 x2，因此输入层的输入个数为2。输入个数也叫特征数或特征向量维度。输出结果为y，所以输出层的输出个数为1。

∇劈形算符，就是对倒三角后面的量做如下操作：表示对函数在各个正交方向上求导数以后再分别乘上各个方向上的单位向量

（相关公式直接抄自开头所提到的开源资料中，有兴趣大家可以推导试试）

线性回归的从零开始实现

（各种解释都在代码中了，代码源自引文～）

import tensorflow as tf
print(tf.__version__)
from matplotlib import pyplot as plt
import random
num_inputs = 2
num_examples = 1000
#实际参数
true_w = [2, -3.4]
true_b = 4.2
#1.x版本
#sess = tf.Session()
#2.0版本
sess=tf.compat.v1.Session()
# tf.random_normal()函数用于从“服从指定正态分布的序列”中随机取出指定个数的值。
# tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
# shape: 输出张量的形状，必选
# mean: 正态分布的均值，默认为0
# stddev: 正态分布的标准差，默认为1.0
# dtype: 输出的类型，默认为tf.float32
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样
# name: 操作的名称

#1.x:random_normal
features = tf.random.normal((num_examples, num_inputs),stddev = 1)
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += tf.random.normal(labels.shape,stddev=0.01)

#随机返回batch_size个随机个样例+特征值
def data_iter(batch_size, features, labels):
    #num_examples = len(features)
    num_examples = features.shape[0]
    indices = list(range(num_examples))
    #shuffle() 方法将序列的所有元素随机排序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        #以batch_size=10为例子， 将数据划分为0 - 10, 10 - 20, 20 - 30等
        j = indices[i: min(i+batch_size, num_examples)]
        #params，按照axis坐标和indices标注的元素下标，把这些元素抽取出来组成新的tensor.
        #yield的作用： 就是把一个函数变成一个生成器，调用函数时候，输出返回的是一个iterable对象。，yield使得代码简洁的同时， 降低了计算消耗
        yield tf.gather(features, axis=0, indices=j), tf.gather(labels, axis=0, indices=j)
#随机样本数量
batch_size = 10
#提取随机样本并输出看看
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break
#初始化w、b,将权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0
w = tf.Variable(tf.random.normal((num_inputs, 1), stddev=0.01))
b = tf.Variable(tf.zeros((1,)))
#定义模型，其实就是矩阵乘法
def linreg(X, w, b):
    return tf.matmul(X, w) + b
#定义损失函数，y_hat为预测值，y为实际值
def squared_loss(y_hat, y):
    return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 /2
#优化函数，此方法为小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数，这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和，我们将它除以批量大小来得到平均值
def sgd(params, lr, batch_size, grads):
    """Mini-batch stochastic gradient descent."""
    for i, param in enumerate(params):
        param.assign_sub(lr * grads[i] / batch_size)
#lr学习率，num_epochs训练轮数，net模型名称，loss损失函数名
lr = 0.03
num_epochs = 30
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        with tf.GradientTape() as t:
            #w、b由tf.Variable创建，无需watch，如果为tf.constant或者tf.convert_to_tensor创建则需要watch
            #t.watch([w,b])
            #计算损失
            l = loss(net(X, w, b), y)
        #计算梯度
        grads = t.gradient(l, [w, b])
        #使用优化算法
        sgd([w, b], lr, batch_size, grads)
    #train_l是全部的损失值的数组,1000*1
    train_l = loss(net(features, w, b), labels)
    #print(train_l)
    #print(train_l.shape)
    print('epoch %d, loss %f' % (epoch + 1, tf.reduce_mean(train_l)))
print(true_w, w)
print(true_b, b)

线性回归的简洁实现

（各种解释都在代码中了，代码源自引文～）

import tensorflow as tf

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = tf.random.normal(shape=(num_examples, num_inputs), stddev=1)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += tf.random.normal(labels.shape, stddev=0.01)

from tensorflow import data as tfdata

batch_size = 10
# Dataset.from_tensor_slices，将训练数据的特征和标签组合
dataset = tfdata.Dataset.from_tensor_slices((features, labels))
# 随机读取小批量
#shuffle 的 buffer_size 参数应大于等于样本数
dataset = dataset.shuffle(buffer_size=num_examples)
#batch 可以指定 batch_size 的分割大小，分割为10个10个的小组
dataset = dataset.batch(batch_size)

#输出分组看看
#enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，返回值为索引值+遍历对象的对应索引内容
for (batch, (X, y)) in enumerate(dataset):
    print(X, y)
    break
#Tensorflow 2.0推荐使用Keras定义网络
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow import initializers as init
model = keras.Sequential()
#Keras 中初始化参数由 kernel_initializer 和 bias_initializer 选项分别设置权重和偏置的初始化方式。
# RandomNormal(stddev=0.01)指定权重参数每个元素将在初始化时随机采样于均值为0、标准差为0.01的正态分布。
# bias_initializer不设置，偏差参数默认会初始化为零。
model.add(layers.Dense(1, kernel_initializer=init.RandomNormal(stddev=0.01)))
#设置损失函数，均方误差损失
from tensorflow import losses
loss = losses.MeanSquaredError()
#设置优化器及学习率，小批量随机梯度下降（SGD）
from tensorflow.keras import optimizers
trainer = optimizers.SGD(learning_rate=0.1)
#训练次数
num_epochs = 30
#在使用Tensorflow训练模型时，我们通过调用tensorflow.GradientTape记录动态图梯度，执行tape.gradient获得动态图中各变量梯度。
# 通过 model.trainable_variables 找到需要更新的变量，并用 trainer.apply_gradients 更新权重，完成一步训练
for epoch in range(1, num_epochs + 1):
    for (batch, (X, y)) in enumerate(dataset):
        with tf.GradientTape() as tape:
            l = loss(model(X, training=True), y)
        #model.trainable_variables会获得需要用的量
        #获得梯度
        grads = tape.gradient(l, model.trainable_variables)
        #apply_gradients更新权重
        trainer.apply_gradients(zip(grads, model.trainable_variables))

    l = loss(model(features), labels)
    print('epoch %d, loss: %f' % (epoch, l))