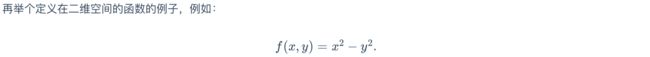动手学深度学习(tensorflow)---学习笔记整理(九、优化算法篇)
有关公式、基本理论等大量内容摘自《动手学深度学习》(TF2.0版))
优化与深度学习
优化在深度学习中有很多挑战。下面描述了其中的两个挑战,即局部最小值和鞍点。
局部最小值
运行代码:
import sys
import tensorflow as tf
sys.path.append("..")
from mpl_toolkits import mplot3d # 三维画图
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from IPython import display
from matplotlib import pyplot as plt
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#局部最小值
def f(x):
return x * np.cos(np.pi * x)
set_figsize((4.5, 2.5))
x = np.arange(-1.0, 2.0, 0.1)
fig, = plt.plot(x, f(x))
fig.axes.annotate('local minimum', xy=(-0.3, -0.25), xytext=(-0.77, -1.0),
arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum', xy=(1.1, -0.95), xytext=(0.6, 0.8),
arrowprops=dict(arrowstyle='->'))
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()
结果:
鞍点
代码:
import sys
import tensorflow as tf
sys.path.append("..")
from mpl_toolkits import mplot3d # 三维画图
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from IPython import display
from matplotlib import pyplot as plt
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#鞍点
x = np.arange(-2.0, 2.0, 0.1)
fig, = plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52, -5.0),
arrowprops=dict(arrowstyle='->'))
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()
结果:
代码:
import sys
import tensorflow as tf
sys.path.append("..")
from mpl_toolkits import mplot3d # 三维画图
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from IPython import display
from matplotlib import pyplot as plt
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#马鞍面
x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2
ax = plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'rx')
ticks = [-1, 0, 1]
plt.xticks(ticks)
plt.yticks(ticks)
ax.set_zticks(ticks)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
结果:
如果三维图片生成结果为一条线,如图所示:
取消下列选项即可生成三维图片
小结:
- 由于优化算法的目标函数通常是一个基于训练数据集的损失函数,优化的目标在于降低训练误差。
- 由于深度学习模型参数通常都是高维的,目标函数的鞍点通常比局部最小值更常见。
下面来谈谈具体的优化算法~~
梯度下降
一维梯度下降
![]()
代码如下:
import numpy as np
import tensorflow as tf
import math
from matplotlib import pyplot as plt
import sys
from IPython import display
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
def gd(eta):
x = 10
results = [x]
for i in range(10):
x -= eta * 2 * x # f(x) = x * x的导数为f'(x) = 2 * x
results.append(x)
print('epoch 10, x:', x)
return results
res = gd(0.2)
def show_trace(res,s=None):
s=str(s)
n = max(abs(min(res)), abs(max(res)), 10)
f_line = np.arange(-n, n, 0.1)
set_figsize()
plt.plot(f_line, [x * x for x in f_line])
plt.plot(res, [x * x for x in res], '-o')
plt.xlabel('x'+':'+s)
plt.ylabel('f(x)')
plt.show()
show_trace(gd(0.1),0.1)
show_trace(gd(0.3),0.3)
show_trace(gd(0.5),0.5)
show_trace(gd(0.7),0.7)
show_trace(gd(0.9),0.9)
show_trace(gd(1.1),1.1)
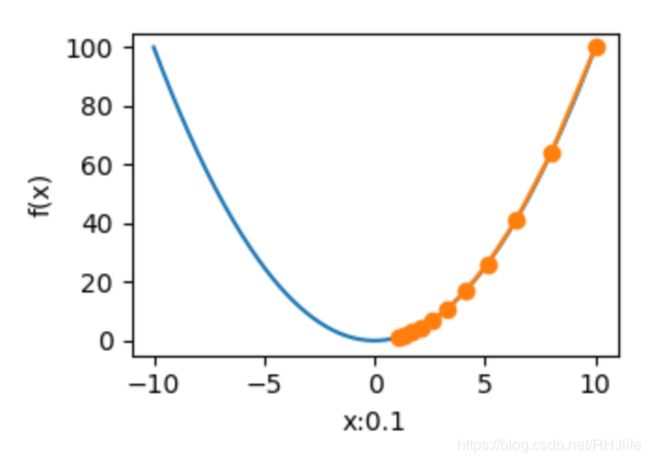
show_trace(gd(1.3),1.3)通过不同的学习率我们来进行观察
epoch 10, x: 0.06046617599999997
epoch 10, x: 1.0737418240000003
epoch 10, x: 0.0010485760000000007
epoch 10, x: 0.0
epoch 10, x: 0.0010485759999999981
epoch 10, x: 1.0737418240000007
epoch 10, x: 61.917364224000096
epoch 10, x: 1099.5116277760003通过上述损失和图像我们可以发现,学习率越小,其逼近最小值点越慢,在学习率为0.5时正好落到了最小值点处(如果是局部最小值点,就出不来,如果最小值点,就是完美值了)。0.7时,可以发现第一次越过了最小值点,后续慢慢趋于最小值,而0.9和1.1点则使loss越来越多,原因是每次更新的值由学习率和梯度决定,0.7由于初始值*学习率比较大,所以跨度比较大,但是第二个点的梯度很小,所以慢慢收敛,而学习率过大则会导致第二点的梯度很大,下次更新是跳跃值更大,导致后续点梯度越来越大。例如学习率1.5时:loss=10240.0,图像如下:
学习率
通过上述不同学习率图像进行对比,我们可以发现一些规律:学习率越小,越容易逼近最小值,但是太小了有两个问题,一是容易陷入局部最小值出不来,二是需要大量轮次训练才可以;学习率越大,而可能出现loss增大的现象。学会调整学习率来寻找最优解是至关重要的。
多维梯度下降
代码如下:
import numpy as np
import tensorflow as tf
import math
from matplotlib import pyplot as plt
import sys
from IPython import display
#二维绘图
def train_2d(trainer,eta):
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态,本章后续几节会使用
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2,eta)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
def show_trace_2d(f, results):
plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def f_2d(x1, x2): # 目标函数
return x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2,eta):
return (x1 - eta * 2 * x1, x2 - eta * 4 * x2, 0, 0)
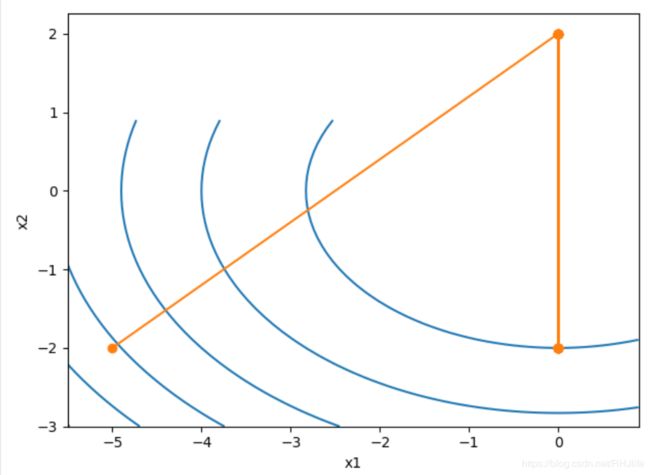
show_trace_2d(f_2d, train_2d(gd_2d,0.1))
show_trace_2d(f_2d, train_2d(gd_2d,0.3))
show_trace_2d(f_2d, train_2d(gd_2d,0.5))
show_trace_2d(f_2d, train_2d(gd_2d,0.7))
下面图片依次为学习率0.1、0.3、0.5、0.7的轨迹图
通过上述可以发现,学习率为0.1和0.3时,loss不断减少,x1x2轴都在不断收敛,0.5时收敛到0,完美值,而0.7而在x2上发生发散,结论与一维时相似,而此规律可以反映到多维上的。
随机梯度下降
下面图片依次为学习率0.1、0.3、0.5、0.7的轨迹图
通过观察随机梯度下降中自变量的迭代轨迹相对于梯度下降中的来说更为曲折。这是由于实验所添加的噪声使模拟的随机梯度的准确度下降。在实际中,这些噪声通常指训练数据集中的无意义的干扰。
小结:
- 使用适当的学习率,沿着梯度反方向更新自变量可能降低目标函数值。梯度下降重复这一更新过程直到得到满足要求的解。
- 学习率过大或过小都有问题。一个合适的学习率通常是需要通过多次实验找到的。
- 当训练数据集的样本较多时,梯度下降每次迭代的计算开销较大,因而随机梯度下降通常更受青睐。
小批量随机梯度下降
本章里我们将使用一个来自NASA的测试不同飞机机翼噪音的数据集来比较各个优化算法
从零开始实现:
import numpy as np
import time
import tensorflow as tf
from matplotlib import pyplot as plt
from IPython import display
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#获取前1500个数据库
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
features,labels = get_data_ch7()
print(features.shape)
def sgd(params, states,hyperparams,grads):
for i,p in enumerate(params):
p.assign_sub(hyperparams['lr'] * grads[i])
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = linreg, squared_loss
w = tf.Variable(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=tf.float32)
b = tf.Variable(tf.zeros(1,dtype=tf.float32))
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features, w, b), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features,labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X, w, b), y)) # 使用平均损失
grads = tape.gradient(l, [w,b])
optimizer_fn([w, b], states, hyperparams,grads) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
def train_sgd(lr, batch_size, num_epochs=2):
train_ch7(sgd, None, {'lr': lr}, features, labels, batch_size, num_epochs)
#学习率为1,梯度下降,6轮
train_sgd(1, 1500, 6)
#学习率为0.005,随机梯度下降,2轮
train_sgd(0.005, 1,6)
#学习率为0.005,小批量随机梯度下降,2轮
train_sgd(0.005, 10,6)
结果图:
梯度下降的1个迭代周期对模型参数只迭代1次。可以看到6次迭代后目标函数值(训练损失)的下降趋向了平稳
当批量大小为1时,优化使用的是随机梯度下降。未对学习率进行自我衰减,而是直接采用较小的常数学习率。随机梯度下降中,每处理一个样本会更新一次自变量(模型参数),一个迭代周期里会对自变量进行1,500次更新。可以看到,目标函数值的下降过程比较颠簸,也如我们之前展示的那样。
虽然随机梯度下降和梯度下降在一个迭代周期里都处理了1,500个样本,但实验中随机梯度下降的一个迭代周期耗时更多。这是因为随机梯度下降在一个迭代周期里做了更多次的自变量迭代,而且单样本的梯度计算难以有效利用矢量计算。
当批量大小为10时,优化使用的是小批量随机梯度下降。它在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间
简洁实现:
from tensorflow.keras import optimizers
from matplotlib import pyplot as plt
from IPython import display
import tensorflow as tf
import numpy as np
import time
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#获取前1500个数据库
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
features,labels = get_data_ch7()
trainer = optimizers.SGD(learning_rate=0.05)
def train_tensorflow2_ch7(trainer_name, trainer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1))
loss = tf.losses.MeanSquaredError()
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features,labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
# 创建Trainer实例来迭代模型参数
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X), y)) # 使用平均损失
grads = tape.gradient(l, net.trainable_variables)
trainer.apply_gradients(zip(grads, net.trainable_variables)) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
#使用
train_tensorflow2_ch7(trainer, {"lr": 0.05}, features, labels, 10)
小结:
- 小批量随机梯度每次随机均匀采样一个小批量的训练样本来计算梯度。
- 在实际中,(小批量)随机梯度下降的学习率可以在迭代过程中自我衰减。
- 通常,小批量随机梯度在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。
动量法
梯度下降的问题
import numpy as np
import time
import sys
import tensorflow as tf
from matplotlib import pyplot as plt
eta = 0.4 # 学习率
def show_trace_2d(f, results):
plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def train_2d(trainer):
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态,本章后续几节会使用
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)
show_trace_2d(f_2d, train_2d(gd_2d))
结果:
可以看到,同一位置上,目标函数在竖直方向(x2x2x2轴方向)比在水平方向(x1x1x1轴方向)的斜率的绝对值更大。因此,给定学习率,梯度下降迭代自变量时会使自变量在竖直方向比在水平方向移动幅度更大。那么,我们需要一个较小的学习率从而避免自变量在竖直方向上越过目标函数最优解。然而,这会造成自变量在水平方向上朝最优解移动变慢。
试着将学习率调得稍大一点(学习率为0.6),此时自变量在竖直方向不断越过最优解并逐渐发散,如下图:
import numpy as np
import time
import sys
import tensorflow as tf
from matplotlib import pyplot as plt
eta = 0.6 # 学习率
def show_trace_2d(f, results):
plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def train_2d(trainer):
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态,本章后续几节会使用
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)
def momentum_2d(x1, x2, v1, v2):
v1 = gamma * v1 + eta * 0.2 * x1
v2 = gamma * v2 + eta * 4 * x2
return x1 - v1, x2 - v2, v1, v2
eta, gamma = 0.4, 0.5
show_trace_2d(f_2d, train_2d(momentum_2d))
eta, gamma = 0.6, 0.5
show_trace_2d(f_2d, train_2d(momentum_2d))
结果如下:(学习率0.4、0.6和gamma=0.5)
可以看到使用较小的学习率η=0.4η=0.4η=0.4和动量超参数γ=0.5γ=0.5γ=0.5时,动量法在竖直方向上的移动更加平滑,且在水平方向上更快逼近最优解。下面使用较大的学习率η=0.6η=0.6η=0.6,此时自变量也不再发散。
指数加权移动平均(动量法原理)
说白了就是,把近期的影响考虑进来,不使用动量法时,x2轴上波动较大。考虑动力法时,从第二个数值开始,考虑第一次较大的波动,会让第二次波动较小,第三次波动考虑第一次波动时影响远不如第二次波动,第二次波动已经比较平稳,所以后续波动都会比较稳定下来。在x1轴由于方向相同,其实影响很小,但是使用较大学习率时,x1轴就会较快收敛,而x2轴还不会发散,就可以达到我们快速收敛的目的。
对于参数gamma,则可以看成对(1/1-gamma)加权平均(例如:0.95->20次,0.9->10次,0.5-〉2次)
import numpy as np
import time
import sys
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras import optimizers
eta = 0.6 # 学习率
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
def show_trace_2d(f, results):
plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def train_2d(trainer):
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态,本章后续几节会使用
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
features, labels = get_data_ch7()
def init_momentum_states():
v_w = tf.zeros((features.shape[1], 1))
v_b = tf.zeros(1)
return (v_w, v_b)
def sgd_momentum(params, states, hyperparams, grads):
i = 0
for p, v in zip(params, states):
v = hyperparams['momentum'] * v + hyperparams['lr'] * grads[i]
p.assign_sub(v)
i += 1
def init_momentum_states():
v_w = tf.zeros((features.shape[1], 1))
v_b = tf.zeros(1)
return (v_w, v_b)
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = linreg, squared_loss
w = tf.Variable(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=tf.float32)
b = tf.Variable(tf.zeros(1, dtype=tf.float32))
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features, w, b), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X, w, b), y)) # 使用平均损失
grads = tape.gradient(l, [w, b])
optimizer_fn([w, b], states, hyperparams, grads) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
features,labels = get_data_ch7()
trainer = optimizers.SGD(learning_rate=0.05)
train_ch7(sgd_momentum, init_momentum_states(),
{'lr': 0.02, 'momentum': 0.5}, features, labels)
简单实现(在Tensorflow中,只需要通过参数momentum来指定动量超参数即可使用动量法。):
import numpy as np
import time
import sys
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras import optimizers
trainer = optimizers.SGD(learning_rate=0.004,momentum=0.9)
eta = 0.6 # 学习率
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
def train_tensorflow2_ch7(trainer_name, trainer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1))
loss = tf.losses.MeanSquaredError()
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
# 创建Trainer实例来迭代模型参数
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X), y)) # 使用平均损失
grads = tape.gradient(l, net.trainable_variables)
trainer.apply_gradients(zip(grads, net.trainable_variables)) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
features,labels = get_data_ch7()
train_tensorflow2_ch7(trainer, {'lr': 0.004, 'momentum': 0.9},
features, labels)
小结:
- 动量法使用了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均,且权重按时间步指数衰减。
- 动量法使得相邻时间步的自变量更新在方向上更加一致。
AdaGrad算法
import numpy as np
import math
import sys
from matplotlib import pyplot as plt
def show_trace_2d(f, results):
plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def train_2d(trainer):
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态,本章后续几节会使用
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
def adagrad_2d(x1, x2, s1, s2):
g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6 # 前两项为自变量梯度
s1 += g1 ** 2
s2 += g2 ** 2
x1 -= eta / math.sqrt(s1 + eps) * g1
x2 -= eta / math.sqrt(s2 + eps) * g2
return x1, x2, s1, s2
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
eta = 0.4
show_trace_2d(f_2d, train_2d(adagrad_2d))
eta = 2
show_trace_2d(f_2d, train_2d(adagrad_2d))
结果:
说直白点就是学习率不断下降,下降速度和当前梯度有关系,但是一直下降过程中,后期容易陷入局部最优解出不来的地步。
从零开始实现:(![]() )
)
import numpy as np
import math
import sys
from matplotlib import pyplot as plt
import tensorflow as tf
from IPython import display
import time
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
features, labels = get_data_ch7()
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
def init_adagrad_states():
s_w = tf.zeros((features.shape[1],1),dtype=tf.float32)
s_b = tf.zeros(1,dtype=tf.float32)
return (s_w, s_b)
def adagrad(params, states, hyperparams,grads):
eps = 1e-6
i=0
for p, s in zip(params, states):
s += (grads[i]**2)
p.assign_sub(hyperparams['lr']*grads[i]/tf.sqrt(s+eps))
i+=1
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = linreg, squared_loss
w = tf.Variable(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=tf.float32)
b = tf.Variable(tf.zeros(1, dtype=tf.float32))
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features, w, b), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X, w, b), y)) # 使用平均损失
grads = tape.gradient(l, [w, b])
optimizer_fn([w, b], states, hyperparams, grads) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
train_ch7(adagrad, init_adagrad_states(), {'lr': 0.1}, features, labels)
简单实现(通过名称为Adagrad的优化器方法,我们便可使用Tensorflow2提供的AdaGrad算法来训练模型):
import numpy as np
import time
import sys
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras import optimizers
trainer = optimizers.Adagrad(learning_rate=0.01)
eta = 0.6 # 学习率
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
def train_tensorflow2_ch7(trainer_name, trainer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1))
loss = tf.losses.MeanSquaredError()
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
# 创建Trainer实例来迭代模型参数
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X), y)) # 使用平均损失
grads = tape.gradient(l, net.trainable_variables)
trainer.apply_gradients(zip(grads, net.trainable_variables)) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
features,labels = get_data_ch7()
train_tensorflow2_ch7(trainer, {'lr': 0.004, 'momentum': 0.9},
features, labels)
小结:
- AdaGrad算法在迭代过程中不断调整学习率,并让目标函数自变量中每个元素都分别拥有自己的学习率。
- 使用AdaGrad算法时,自变量中每个元素的学习率在迭代过程中一直在降低(或不变)
RMSProp算法
说白了就是,AdaGrad算法更新学习率会越来越小,而RMSProp算法是AdaGrad算法和加权平均的结合,使得态度对当前的影响变低,可以更快的逼近最优解。
import numpy as np
import time
import math
import sys
import tensorflow as tf
from matplotlib import pyplot as plt
def train_2d(trainer): # 本函数将保存在d2lzh_tensorflow2包中方便以后使用
x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态,本章后续几节会使用
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
def show_trace_2d(f, results): # 本函数将保存在d2lzh_tensorflow2包中方便以后使用
plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def rmsprop_2d(x1, x2, s1, s2):
g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6
s1 = gamma * s1 + (1 - gamma) * g1 ** 2
s2 = gamma * s2 + (1 - gamma) * g2 ** 2
x1 -= eta / math.sqrt(s1 + eps) * g1
x2 -= eta / math.sqrt(s2 + eps) * g2
return x1, x2, s1, s2
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
eta, gamma = 0.4, 0.9
show_trace_2d(f_2d, train_2d(rmsprop_2d))
手动实现:
import numpy as np
import math
import sys
from matplotlib import pyplot as plt
import tensorflow as tf
from IPython import display
import time
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
features, labels = get_data_ch7()
def init_rmsprop_states():
s_w = tf.zeros((features.shape[1],1),dtype=tf.float32)
s_b = tf.zeros(1,dtype=tf.float32)
return (s_w, s_b)
def rmsprop(params, states, hyperparams,grads):
gamma, eps, i = hyperparams['gamma'], 1e-6, 0
for p, s in zip(params, states):
s=gamma*s+(1-gamma)*(grads[i])**2
p.assign_sub(hyperparams['lr']*grads[i]/tf.sqrt(s+eps))
i+=1
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = linreg, squared_loss
w = tf.Variable(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=tf.float32)
b = tf.Variable(tf.zeros(1, dtype=tf.float32))
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features, w, b), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X, w, b), y)) # 使用平均损失
grads = tape.gradient(l, [w, b])
optimizer_fn([w, b], states, hyperparams, grads) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
train_ch7(rmsprop, init_rmsprop_states(), {'lr': 0.01, 'gamma': 0.9},
features, labels)
简单实现(通过名称为RMSprop的优化器方法,我们便可使用Tensorflow2中提供的RMSProp算法来训练模型。注意,超参数γγγ通过alpha指定。):
import numpy as np
import time
import sys
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras import optimizers
trainer = optimizers.RMSprop(learning_rate=0.01,rho=0.9)
eta = 0.6 # 学习率
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
def train_tensorflow2_ch7(trainer_name, trainer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1))
loss = tf.losses.MeanSquaredError()
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
# 创建Trainer实例来迭代模型参数
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X), y)) # 使用平均损失
grads = tape.gradient(l, net.trainable_variables)
trainer.apply_gradients(zip(grads, net.trainable_variables)) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
features,labels = get_data_ch7()
train_tensorflow2_ch7(trainer, {'lr': 0.004, 'momentum': 0.9},
features, labels)
小结:
- RMSProp算法和AdaGrad算法的不同在于,RMSProp算法使用了小批量随机梯度按元素平方的指数加权移动平均来调整学习率。
AdaDelta算法
从零开始实现:(![]() )
)
import numpy as np
import math
import sys
from matplotlib import pyplot as plt
import tensorflow as tf
from IPython import display
import time
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
features, labels = get_data_ch7()
def init_adadelta_states():
s_w, s_b = np.zeros((features.shape[1], 1), dtype=float), np.zeros(1, dtype=float)
delta_w, delta_b = np.zeros((features.shape[1], 1), dtype=float), np.zeros(1, dtype=float)
return ((s_w, delta_w), (s_b, delta_b))
def adadelta(params, states, hyperparams,grads):
rho, eps,i = hyperparams['rho'], 1e-5, 0
for p, (s, delta) in zip(params, states):
s[:] = rho * s + (1 - rho) * (grads[i]**2)
g = grads[i] * np.sqrt((delta + eps) / (s + eps))
p.assign_sub(g)
delta[:] = rho * delta + (1 - rho) * g * g
i+=1
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = linreg, squared_loss
w = tf.Variable(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=tf.float32)
b = tf.Variable(tf.zeros(1, dtype=tf.float32))
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features, w, b), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X, w, b), y)) # 使用平均损失
grads = tape.gradient(l, [w, b])
optimizer_fn([w, b], states, hyperparams, grads) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
train_ch7(adadelta, init_adadelta_states(), {'rho': 0.9}, features, labels)
简单实现:(通过名称为Adadelta的优化器方法,我们便可使用Tensorflow2提供的AdaDelta算法)
import numpy as np
import time
import sys
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras import optimizers
trainer = optimizers.Adadelta(learning_rate=0.01,rho=0.9)
eta = 0.6 # 学习率
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
def train_tensorflow2_ch7(trainer_name, trainer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1))
loss = tf.losses.MeanSquaredError()
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
# 创建Trainer实例来迭代模型参数
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X), y)) # 使用平均损失
grads = tape.gradient(l, net.trainable_variables)
trainer.apply_gradients(zip(grads, net.trainable_variables)) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
features,labels = get_data_ch7()
train_tensorflow2_ch7(trainer, {'lr': 0.004, 'momentum': 0.9},
features, labels)
Adam算法
通过上述公式,其实就是RMSPro算法中的更新x时的梯度,变成了动量法中的v(考虑最近1/1-gamma次梯度)了。
从零开始实现:(![]() )
)
import numpy as np
import math
import sys
from matplotlib import pyplot as plt
import tensorflow as tf
from IPython import display
import time
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
features, labels = get_data_ch7()
def init_adam_states():
v_w, v_b = np.zeros((features.shape[1], 1), dtype=float), np.zeros(1, dtype=float)
s_w, s_b = np.zeros((features.shape[1], 1), dtype=float), np.zeros(1, dtype=float)
return ((v_w, s_w), (v_b, s_b))
def adam(params, states, hyperparams, grads):
beta1, beta2, eps, i = 0.9, 0.999, 1e-6, 0
for p, (v, s) in zip(params, states):
v[:] = beta1 * v + (1 - beta1) * grads[i]
s[:] = beta2 * s + (1 - beta2) * grads[i]**2
v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
p.assign_sub(hyperparams['lr']*v_bias_corr/(np.sqrt(s_bias_corr) + eps))
i+=1
hyperparams['t'] += 1
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = linreg, squared_loss
w = tf.Variable(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=tf.float32)
b = tf.Variable(tf.zeros(1, dtype=tf.float32))
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features, w, b), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X, w, b), y)) # 使用平均损失
grads = tape.gradient(l, [w, b])
optimizer_fn([w, b], states, hyperparams, grads) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
train_ch7(adam, init_adam_states(), {'lr': 0.01, 't': 1}, features,labels)
简单实现:(通过名称为“adam”的Trainer实例,我们便可使用Tensorflow2提供的Adam算法)
import numpy as np
import time
import sys
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras import optimizers
trainer = optimizers.Adam(learning_rate=0.01)
eta = 0.6 # 学习率
def use_svg_display():
"""Use svg format to display plot in jupyter"""
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
#初始化一个线性回归模型
def linreg(X, w, b):
return tf.matmul(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
def get_data_ch7():
data = np.genfromtxt('/Users/ren/PycharmProjects/入组学习/动手学深度学习/data/airfoil_self_noise.dat', delimiter='\t')
#标准化
data = (data - data.mean(axis=0)) / data.std(axis=0)
return tf.convert_to_tensor(data[:1500, :-1],dtype=tf.float32), tf.convert_to_tensor(data[:1500, -1],dtype=tf.float32)
def train_tensorflow2_ch7(trainer_name, trainer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1))
loss = tf.losses.MeanSquaredError()
def eval_loss():
return np.array(tf.reduce_mean(loss(net(features), labels)))
ls = [eval_loss()]
data_iter = tf.data.Dataset.from_tensor_slices((features, labels)).batch(batch_size)
data_iter = data_iter.shuffle(100)
# 创建Trainer实例来迭代模型参数
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
with tf.GradientTape() as tape:
l = tf.reduce_mean(loss(net(X), y)) # 使用平均损失
grads = tape.gradient(l, net.trainable_variables)
trainer.apply_gradients(zip(grads, net.trainable_variables)) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
set_figsize()
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
features,labels = get_data_ch7()
train_tensorflow2_ch7(trainer, {'lr': 0.004, 'momentum': 0.9},
features, labels)
小结:
- Adam算法在RMSProp算法的基础上对小批量随机梯度也做了指数加权移动平均。
- Adam算法使用了偏差修正。
总结:
这些优化算法可有好处,不一定越靠后的越好,选择时应该先选择自己擅长的优化算法,这样懂原理更容易去调参数,如果都不理想,可以更好算法。