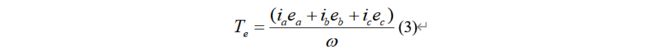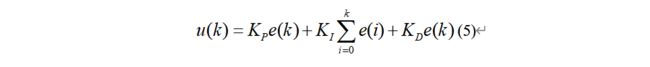基于模糊优化的PID直流无刷电机控制研究
目录
1. 介绍
2 直流无刷电机数学模型建立
3. 直流无刷电机模糊PID控制器设计
4. 仿真实验
5. 结束语
参考文献:
摘要:针对传统PID控制的直流无刷电机调速系统存在响应速度慢,控制效果不佳等问题,设计了基于模糊优化的PID调速系统。本文分析了直流无刷电机基本工作原理,经过模糊自整定PID优化控制器调节输出值,通过改变PWM控制信号的占空比来控制功率MOSFET管的导通与关断,进而实现直流无刷电机的速度控制。在MATLAB-Simlink环境下,搭建直流无刷电机调速系统仿真模型,分别将传统PID控制和采用模糊优化的PID控制进行仿真比较,结果表明在模糊优化的PID控制下,系统响应速度快,无超调,控制效果好。
关键词:直流无刷电机 模糊PID控制 MATLAB仿真
1. 介绍
直流无刷电机具有体积小、扭矩大、效率高,节能环保使用寿命长等优点,广泛应用于工业设备、医疗器械以及新型产业设备等领域[1]。在直流无刷电机调速系统中,通常采用传统PID调节,传统的PID控制器对参数敏感,只有当控制器参数适合被控系统时,才能获得较好的性能。无刷直流电机是一个多变量的非线性系统,传统PID控制下的调速系统,如果系统状态改变,PID的参数也要改变。因此传统PID控制器的动态性能较差,会导致电机速度响应较慢、控制精度低、很难保证良好的调速效果[2]。
模糊控制[3]的概念是由L.A.Zadeh最先提出,这种算法是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制算法。模糊控制不需要精确的数学模型,同时还可以简单有效的处理系统的非线性问题,因此可以提高控制系统的稳定性和鲁棒性,具有良好的控制效果。本文在MATLAB-Simulink环境下对直流无刷电机控制系统的基础上,提出一种模糊PID控制方案,取代了传统的PID控制器,并通过仿真实验证明,在模糊PID控制下,无刷直流电机具有较好的静态和动态性能,同时也具有快速的响应能力和较强的鲁棒性。
2 直流无刷电机数学模型建立
无刷直流电机主要由电机主体,位置检测器,驱动器和控制器组成。电动机的定子绕组多做成三相对称星形连接,如图一所示,本文中电机为三相六状态,其中L、R、ea、eb、ec是电机A、B、C三相等效电路,Q1、Q2、Q3、Q4、Q5、Q6为六只功率晶体管。三个间隔120度的霍尔传感器霍尔A、霍尔B、霍尔C对称放置在定子上,电机转子转动一周,三个霍尔传感器分别产生相差120度的位置方波信号,控制器对霍尔信号进行处理,计算出电机转速,产生三相换相逻辑信号,触发MOSFET功率晶体管导通。通过逆变器给供电,使电机输出连续的转矩和功率。
在不考虑涡流损耗和磁滞损耗,建立直流无刷电机数学模型是由电压微分方程、电磁转矩方程以及电机运动方程组成[4]。忽略涡流和磁滞损耗,忽略齿槽以及换向过程的电磁干扰,假设电机三项绕组完全对称,可以得到直流无刷电机定子三相绕组的电压方程为[5]:
式(1)中,ua、ub、uc为三项相电压;ia、ib、ic为三项相电流;ea、eb、ec为三相反电动势;L为三项绕组的自感;M为每两相绕组间的互感,电机三项采用Y型连接,根据基尔霍夫定律有ia+ib+ic=0,则有Mia+Mib+Mic=0,所以式(1)可化为:
为便于分析,假设不考虑电机转动时的粘滞系数以及电枢绕组的电感。电机输出的电磁转矩方程为:
可以得到运动方程为:
式中ω为电机机械转速,TL为负载转矩,J为系统转动惯量。
3. 直流无刷电机模糊PID控制器设计
直流无刷电机控制系统采用PWM方式对直流无刷电机进行速度控制,传统的电机控制器,如比例积分PI和比例积分微分PID控制器由于结构简单、可靠性高以及易于工程实现目前仍被广泛应用[6]。速度PID控制器可以表示为:
其中e(k)和u(k)是PID控制器的输入和输出,Kp、Ki、Kd分别为比例系数、积分系数和微分系数,PID控制参数一般都在系统运行前已选择好,因此不具有在线整定参数的功能[7]。
模糊PID控制器原理图2所示,根据输入偏差e和偏差变化率ec经推理输出PID修正参数(),完成对PID控制器比例、积分和微分这三个参数ΔKP、ΔKI、ΔKD的在线自整定,控制信号由PID控制器产生,控制信号通过驱动器驱动电机运转,电机的速度信号通过霍尔传感器反馈至控制器,完成速度闭环控制。
输入偏差e和偏差变化率ec和ΔKP、ΔKI、ΔKD的模糊集为:{NB(NegativeBig),NM(NegativeMedium),NS(NegativeSmall),ZO(Zero),PS(PositiveSmall),PM(PositiveMedium),PB(PositiveBig)};
输入变量e和ec的值范围,以及 输出变量kp和ki都是预先确定的 实际的电机控制过程,它们的变化范围是分别进行如下设置。输入偏差e和偏差变化率ec论域取{-3,-2,-1,0,1,2,3},ΔKP的论域取{-3,-2,-1,0,1,2,3}, ΔKI的论域取{-0.9,-0.6,-0.3,0,0.3,0.6,0.9},ΔKD的论域取{-0.6,-0.4,-0.2,0,0.2,0.4,0.6},常用的隶属度函数有三角形、梯形、高斯型,本文输入和输出的隶属度函数均采用对称分布三角形隶属度函数。
模糊控制器的设计主要是总结工程经验[8],为了建立合适的模糊规则表,通常需要遵循以下原则:
当e较大时,为了提高系统的响应速度,需要选择较大的KP,取较小的微分系数KD以防止e较大引起微分溢出,同时也应选择较小的KI以减小积分作用,防止系统超调;
当e和ec为中等时应当适当降低KP以防止系统过度超调,KI和KD应选择中等数值;
当e很小时则需要加大KP和KI以减小e的静态误差,当ec较大时KD可以较小,当ec较小时KD可以取值较大[9][10]。
根据以上原则ΔKP、ΔKI、ΔKD三个参数分别定义模糊规则表如表1所示。
表1 kp模糊规则表
| e |
ec |
||||||
| NB |
NM |
NS |
ZO |
PS |
PM |
PB |
|
| NB |
PB |
PB |
PM |
PM |
PS |
ZO |
ZO |
| NM |
PB |
PB |
PM |
PS |
PS |
ZO |
NS |
| NS |
PM |
PM |
PM |
PS |
ZO |
NS |
NS |
| ZO |
PM |
PM |
PS |
ZO |
NS |
NM |
NM |
| PS |
PS |
PS |
ZO |
NS |
NS |
NM |
NM |
| PM |
PS |
ZO |
NS |
NM |
NM |
NM |
NB |
| PB |
PB |
ZO |
NM |
NM |
NM |
NB |
NB |
表2 ki模糊规则表
| e |
ec |
||||||
| NB |
NM |
NS |
ZO |
PS |
PM |
PB |
|
| NB |
NB |
NB |
NM |
NM |
NS |
ZO |
ZO |
| NM |
NB |
NB |
NM |
NS |
NS |
ZO |
ZO |
| NS |
NB |
NM |
NS |
NS |
ZO |
PS |
PS |
| ZO |
NM |
NM |
NS |
ZO |
PS |
PM |
PM |
| PS |
NM |
NS |
ZO |
PS |
PS |
PM |
PB |
| PM |
ZO |
ZO |
PS |
PS |
PM |
PB |
PB |
| PB |
ZO |
ZO |
PS |
PM |
PM |
PB |
PB |
表3 kd模糊规则表
| e |
ec |
||||||
| NB |
NM |
NS |
ZO |
PS |
PM |
PB |
|
| NB |
PS |
NS |
NB |
NB |
NB |
NM |
PS |
| NM |
PS |
NS |
NB |
NM |
NM |
NS |
ZO |
| NS |
ZO |
NS |
NM |
NM |
NS |
NS |
ZO |
| ZO |
ZO |
NS |
NS |
NS |
NS |
NS |
ZO |
| PS |
ZO |
ZO |
ZO |
ZO |
ZO |
ZO |
ZO |
| PM |
PB |
NS |
PS |
PS |
PS |
PS |
PB |
| PB |
PB |
PM |
PM |
PM |
PS |
PS |
PB |
4. 仿真实验
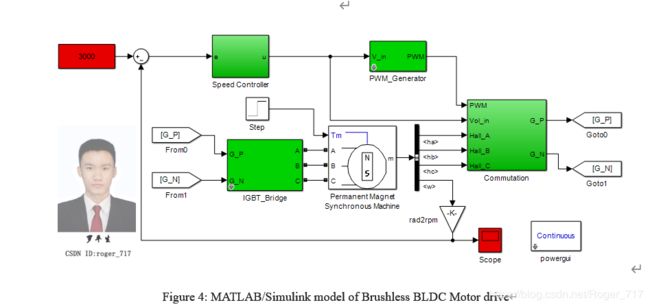
直流无刷电机控制系统通常采用速度电流双闭环控制结构。本文的模型设计采用连续时间系统方法,通过对速度外环的设计,使电机的输出速度跟踪给定的速度值已达到闭环速度控制。在理想条件下,仿真实验在MATLAB/Simlink环境下搭建,无刷直流电机的模型建立如图4所示:
电机由40V直流电源通过三相IGBT逆变器供电,为直观体现改进后的速度控制器控制效果,驱动系统仅由速度闭环组成。电机的选定参数如表1所示。
Table 1: BLDC motor paramete
| Parameters | Value |
| Nominal voltage | 40 V |
| Stator resistance Rs (ohm) | 18.7Ω |
| Stator inductance Ls (H) | 8.5e-3 mH |
| Torque constant | 2.2725 |
| Rated Speed | 3000 rmp |
| Inertia(J) | 2.6e-3 kgm2 |
模糊速度控制器结构如图所示,通过模糊推理机制检测输入偏差e和偏差变化率ec,根据模糊规则推导出优化后的PID参数。
给定电机速度设为3000,通过速度调节器产生输出控制电压,经过PWM转换模块,产生控制方波,根据设定的霍尔换相表,使得所产生的PWM控制电压导通MOSFET管,进而对直流无刷电机进行速度控制。在实验仿真中还增添了外部扰动因素,用以观测速度控制器在外部扰动下的整定效果,通过观察和比较扰动后的整定时间和整定效果,验证控制算法的有效性。
通过观察图12、13、14,起始阶段三种控制器的响应速度较为近似,从波动上来看传统PI控制器较传统PID控制器和模糊PID控制器有超调,且整定时间为14ms。在30ms时突加负载后,传统PI控制器速度曲线波动大。
传统PID控制器无超调,在突加负载后速度曲线相对PI控制器稳定,但速度整定时间为15ms。
模糊PID控制器的速度整定时间为13ms,同时在突加负载情况下速度曲线较稳定。通过以上观察可以得出模糊PID控制器比传统PI控制器、PID控制器稳定性好,在30ms施加负载扰动的情况下,存在轻微转矩脉动,但可快速恢复稳定状态。
5. 结束语
本文通过对BLDC电机的驱动结构进行分析,在分析模糊控制器结构的基础上揭示了模糊控制器与PID控制器之间的关系,在Matlab-Simlink环境下进行了仿真,仿真结果表明模糊PID控制响应速度快,具有良好的稳定性和鲁棒性。
参考文献:
- C, L, Xia, Brushless DC motor control system[M], Eds. Beijing: Science Press, 2005.
- Zhi Chang-Yi, Wang Rui-Ling, Tang Dao-Kui, and Liu Run-Tain, “Study on fuzzy self-adaptive PID control strategy for brushless DC motor,” Power System Protection and Contron, vol. 38, issue 8, pp. 35-37, August 2010.
- L. A. Zadeh, “Fuzzy Sets”, Information and control, 8(3):338-353, 1965.
- Z. C. Ji, Y. X. Shen, J. G. Jiang, A novel method for modeling and simulation of BLDC system based on matlab, Journal of
System Simulation, 2003, 12(15): 1745–1758 - H. Ji and Z. Li, Design of Neural Network PID Controller Based on Brushless DC Motor, Second International Conference on Intelligent Computation Technology and Automation, Vol.3, pp.46-49, October. 2009
- Jack, A.G., Mecrow, B.C., Haylock, J.. A comparative study of permanent magnet and switched reluctance motors for high performance fault tolerant applications [J]. IEEE Trans. Ind. Appliy cat. 1996, 32:889-895
- Z. J. Zheng, N. Wang, Z. Sun. Fuzzy PI Compound of PWM Rectifiers with Applications to Marine Vehicle Electric
Propulsion System [J], International Journal of Fuzzy Systems, 2017, 4:1-10. - Mavungu Masiala ; Behzad Vafakhah. Fuzzy Self-Tuning Speed Control of an Indirect Field-Oriented Control Induction Motor Drive [J], IEEE Transactions on Industry Applications, 2008,1732-1740.
- Choi, Han Ho, Hong Min Yun, and Yong Kim. Implementation of evolutionary fuzzy PID speed controller for PM synchronous motor [J], IEEE Transactions on Industry Informatics. 2015,540-547.
- Chang, Yuan-Chih. Speed Control of the Surface-Mounted Permanent-Magnet Synchronous Motor Based on Takagi-Sugeno Fuzzy Models [J], IEEE Transactions on Power Electronics. 2016,6504-6510.