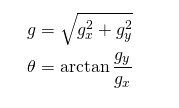深度学习----CNN的图像学习之HOG(方向梯度直方图)详解
- 一、原理
- 二、参数的理解
-
- 2.1、灰度值
- 2.2、归一化
- 2.3、细胞
- 2.4、窗口
- 2.5、类型
- 2.6、Gamma标准化
- 2.7、图像梯度及梯度算子
- 2.8、直方图
- 2.9、高斯空域加窗
-
- 三、步骤及算法
-
- 3.1、数据预处理
- 3.2、计算梯度图像
- 3.3、计算梯度直方图
- 3.4、归一化
- 3.5、计算HOG特征向量
-
- 四、HOG优缺点
(Histogram Of Gradient, 方向梯度直方图)
一、原理
梯度的统计信息,梯度主要存在于边缘的地方
HOG的图像分割策略,一般来说有overlap和non-overlap两种,如下图所示。overlap指的是分割出的区块(patch)互相交叠,有重合的区域。non-overlap指的是区块不交叠,没有重合的区域。
overlap,这种分割方式可以防止对一些物体的切割,还是以眼睛为例,如果分割的时候正好把眼睛从中间切割并且分到了两个patch中,提取完HOG特征之后,这会影响接下来的分类效果,但是如果两个patch之间overlap,那么至少在一个patch会有完整的眼睛。overlap的缺点是计算量大,因为重叠区域的像素需要重复计算。
non-overlap,缺点就是上面提到的,有时会将一个连续的物体切割开,得到不太“好”的HOG特征,优点是计算量小,尤其是与Pyramid(金字塔)结合时,这个优点更为明显。
特征描述子
特征描述子就是图像的表示,抽取了有用的信息丢掉了不相关的信息。通常特征描述子会把一个w*h*3(宽*高*3,3个channel)的图像转换成一个长度为n的向量/矩阵。比如一副64*128*3的图像,经过转换后输出的图像向量长度可以是3780。
什么样子的特征是有用的呢?假设我们想要预测一张图片里面衣服上面的扣子,扣子通常是圆的,而且上面有几个洞,那你就可以用边缘检测(edge detector),把图片变成只有边缘的图像,然后就可以很容易的分辨了,那么对于这张图边缘信息就是有用的,颜色信息就是没有用的。而且好的特征应该能够区分纽扣和其它圆形的东西的区别。
方向梯度直方图(HOG)中,梯度的方向分布被用作特征。沿着一张图片X和Y轴的方向上的梯度是很有用的,因为在边缘和角点的梯度值是很大的,我们知道边缘和角点包含了很多物体的形状信息。
二、参数的理解
2.1、灰度值
指黑白图像中点的颜色深度,范围一般从0到255,白色为255,黑色为0,故黑白图片也称灰度图像

2.2、归一化
图像归一化:
归一化图像的主要目的是提高检测器对光照的鲁棒性,因为实际的人体目标可能出现的各种不同的场合,检测器,必须对光照不太敏感才会有好的效果。
1、转换成标准模式,防止仿射变换的影响。
2、减小几何变换的影响。
3、加快梯度下降求最优解的速度。

2.3、细胞
2.4、窗口
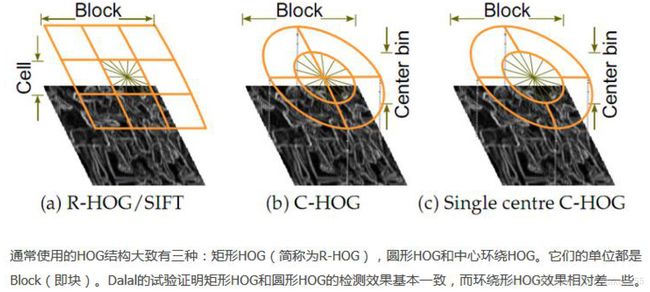
2.5、类型
2.6、Gamma标准化
2.7、图像梯度及梯度算子
图像梯度可以把图像看成二维离散函数,图像梯度其实就是这个二维离散函数的求导:
图像梯度: G(x,y)=dx(i,j)+dy(i,j); G ( x , y ) = d x ( i , j ) + d y ( i , j ) ;
梯度算子介绍点击这里
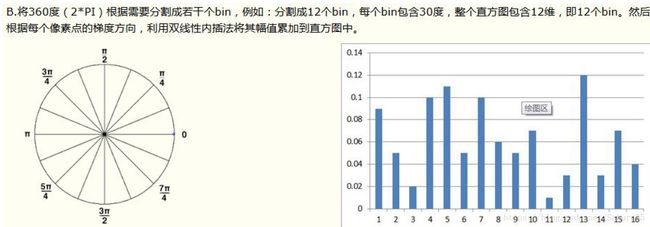
在每个Cell中,我们构建对于方向的投票。方向可以是0~ 180度(无符号的梯度)或者0 ~ 360度(有符号的梯度)。论文中采用的是0 ~ 180度的无符号梯度投票。将0~180度平均分解成9个方向。像素的投票的值是实际梯度大小值。
在投票时为了reduce aliasing,我们会使用线性插值的方法进行投票。例如当前点的方向为65、梯度大小为20,这就需要向60度投票15,向80度投票5.
2.8、直方图
2.9、高斯空域加窗
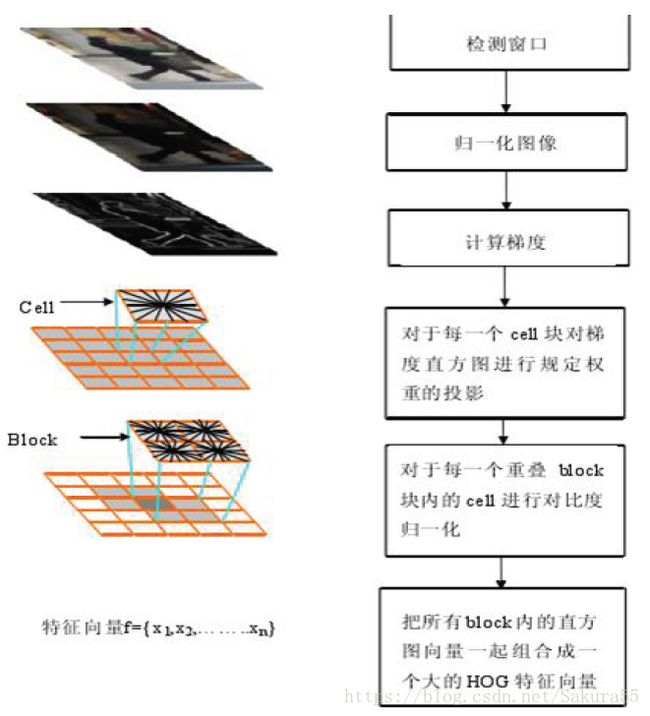
三、步骤及算法
3.1、数据预处理
Patch(窗口)可以是任意的尺寸,但是有一个固定的比列,比如当patch长宽比1:2,那patch大小可以是100*200, 128*256或者1000*2000但不可以是101*205。
这里有张图是720*475的,我们选100*200大小的patch来计算HOG特征,把这个patch从图片里面抠出来,然后再把大小调整成64*128。
3.2、计算梯度图像
首相我们计算水平和垂直方向的梯度,再来计算梯度的直方图。可以用下面的两个kernel来计算,也可以直接用OpenCV里面的kernel大小为1的Sobel算子来计算。

接着,用下面的公式来计算梯度的幅值g和方向theta:
左边:x轴的梯度绝对值 中间:y轴的梯度绝对值 右边:梯度幅值
从上面的图像中可以看到x轴方向的梯度主要凸显了垂直方向的线条,y轴方向的梯度凸显了水平方向的梯度,梯度幅值凸显了像素值有剧烈变化的地方。(注意:图像的原点是图片的左上角,x轴是水平的,y轴是垂直的)
图像的梯度去掉了很多不必要的信息(比如不变的背景色),加重了轮廓。换句话说,你可以从梯度的图像中还是可以轻而易举的发现有个人。
在每个像素点,都有一个幅值(magnitude)和方向,对于有颜色的图片,会在三个channel上都计算梯度。那么相应的幅值就是三个channel上最大的幅值,角度(方向)是最大幅值所对应的角。
3.3、计算梯度直方图
在这一步,上面的patch图像会被分割成8*8大小的网格(如下图),每个网格都会计算一个梯度直方图。那为什么要分成8*8的呢?用特征描述子的一个主要原因是它提供了一个紧凑(compact)/压缩的表示。一个8*8的图像有8*8*3=192个像素值,每个像素有两个值(幅值magnitude和方向direction,三个channel取最大magnitude那个),加起来就是8*8*2=128,后面我们会看到这128个数如何用一个9个bin的直方图来表示成9个数的数组。不仅仅是可以有紧凑的表示,用直方图来表示一个patch也可以更加抗噪,一个gradient可能会有噪音,但是用直方图来表示后就不会对噪音那么敏感了。

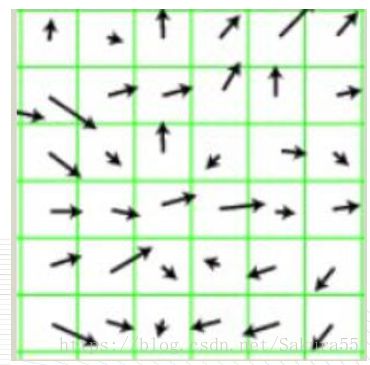
对于64*128的这幅patch来说,8*8的网格已经足够大来表示有趣的特征比如脸,头等等。直方图是有9个bin的向量,代表的是角度0,20,40,60…..160。我们先来看看每个8*8的cell的梯度都是什么样子:

中间: 一个网格用箭头表示梯度 右边: 这个网格用数字表示的梯度
中间这个图的箭头是梯度的方向,长度是梯度的大小,可以发现箭头的指向方向是像素强度都变化方向,幅值是强度变化的大小。
右边的梯度方向矩阵中可以看到角度是0-180度,不是0-360度,这种被称之为”无符号”梯度(“unsigned” gradients)因为一个梯度和它的负数是用同一个数字表示的,也就是说一个梯度的箭头以及它旋转180度之后的箭头方向被认为是一样的。那为什么不用0-360度的表示呢?在事件中发现unsigned gradients比signed gradients在行人检测任务中效果更好。一些HOG的实现中可以让你指定signed gradients。
下一步就是为这些8*8的网格创建直方图,直方图包含了9个bin来对应0,20,40,…160这些角度。
下面这张图解释了这个过程。我们用了上一张图里面的那个网格的梯度幅值和方向。根据方向选择用哪个bin, 根据副值来确定这个bin的大小。先来看蓝色圈圈出来的像素点,它的角度是80,副值是2,所以它在第五个bin里面加了2,再来看红色的圈圈出来的像素点,它的角度是10,副值是4,因为角度10介于0-20度的中间(正好一半),所以把幅值一分为二地放到0和20两个bin里面去。
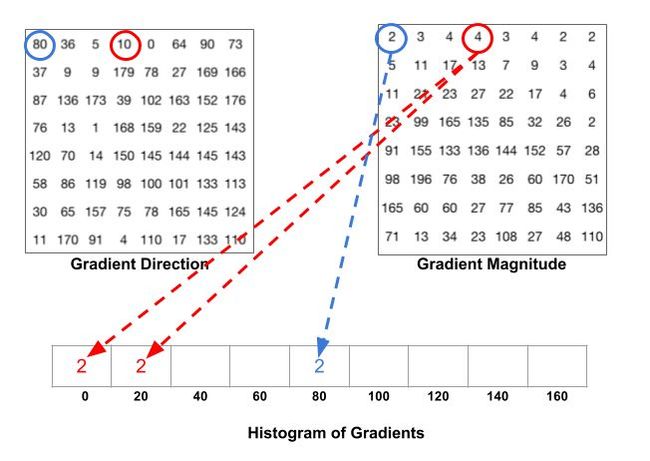
这里有个细节要注意,如果一个角度大于160度,也就是在160-180度之间,我们知道这里角度0,180度是一样的,所以在下面这个例子里,像素的角度为165度的时候,要把幅值按照比例放到0和160的bin里面去。

把这8*8的cell里面所有的像素点都分别加到这9个bin里面去,就构建了一个9-bin的直方图,上面的网格对应的直方图如下:
这里,在我们的表示中,Y轴是0度(从上往下)。你可以看到有很多值分布在0,180的bin里面,这其实也就是说明这个网格中的梯度方向很多都是要么朝上,要么朝下。
3.4、归一化
上面的步骤中,我们创建了基于图片的梯度直方图,但是一个图片的梯度对于整张图片的光线会很敏感。如果你把所有的像素点都除以2,那么梯度的幅值也会减半,那么直方图里面的值也会减半,所以这样并不能消除光线的影响。所以理想情况下,我们希望我们的特征描述子可以和光线变换无关,所以我们就想让我们的直方图归一化从而不受光线变化影响。
先考虑对向量用l2归一化的步骤是:
把v中每一个元素除以146.64得到[0.87,0.43,0.22]
考虑另一个向量2*v,归一化后可以得到向量依旧是[0.87, 0.43, 0.22]。你可以明白归一化是把scale给移除了.
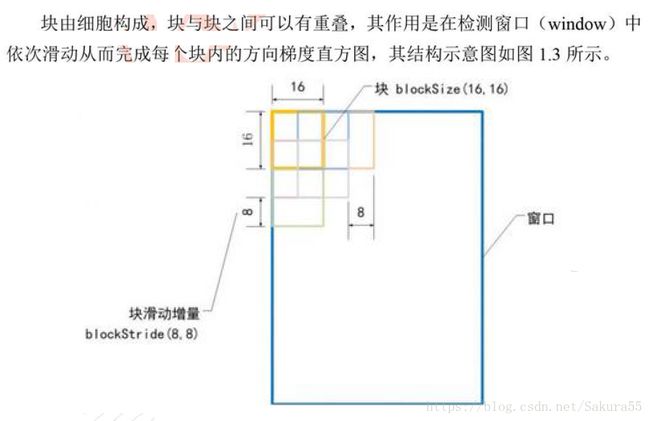
你也许想到直接在我们得到的9*1的直方图上面做归一化,这也可以,但是更好的方法是从一个16*16的块上做归一化,也就是4个9*1的直方图组合成一个36*1的向量,然后做归一化,接着,窗口再朝后面挪8个像素(看动图)。重复这个过程把整张图遍历一边。

3.5、计算HOG特征向量
为了计算这整个patch的特征向量,需要把36*1的向量全部合并组成一个巨大的向量。向量的大小可以这么计算:
我们有多少个16*16的块?水平7个,垂直15个,总共有7*15=105次移动。每个16*16的块代表了36*1的向量。所以把他们放在一起也就是36*105=3780维向量。
可视化HOG
通常HOG特征描述子是画出8*8网格中9*1归一化的直方图,见下图。你可以发现直方图的主要方向捕捉了这个人的外形,特别是躯干和腿。
四、HOG优缺点
优点:
(1)HOG表示的是边缘(梯度)的结构特征,因此可以描述局部的形状信息;
(2)位置和方向空间的量化一定程度上可以抑制平移和旋转带来的影响;
(3)采取在局部区域归一化直方图,可以部分抵消光照变化带来的影响;
(4)由于一定程度忽略了光照颜色对图像造成的影响,使得图像所需要的表征数据的维度降低了;
(5)而且由于这种分块分单元的处理方法,也使得图像局部像素点之间的关系可以很好得到表征。
缺点:
(1)描述子生成过程冗长,导致速度慢,实时性差;
(2)很难处理遮挡问题;
(3)由于梯度的性质,该描述子对噪点相当敏感。
参考 ● (https://www.cnblogs.com/zhazhiqiang/p/3595266.html)
●图像学习-HOG特征(https://blog.csdn.net/leadai/article/details/79092686)
● 方向梯度直方图(HOG,Histogram of Gradient)学习笔记(http://blog.sina.com.cn/s/blog_60e6e3d50101bkpn.html)
● http://www.open-open.com/lib/view/open1440832074794.html