SMOTE__简单原理图示_算法实现及R和Python调包简单实现
一、SMOTE原理
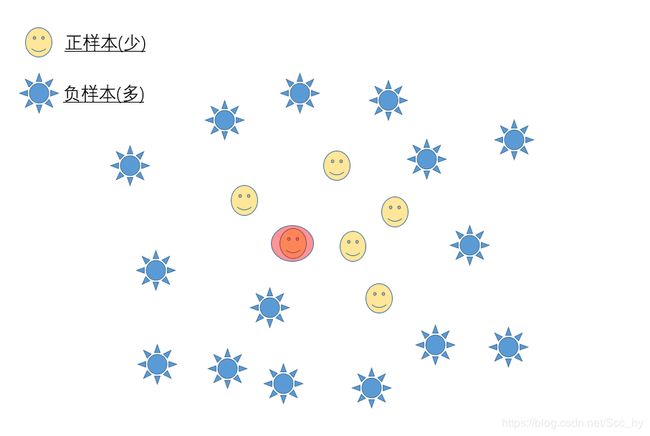
SMOTE的全称是Synthetic Minority Over-Sampling Technique 即“人工少数类过采样法”,非直接对少数类进行重采样,而是设计算法来人工合成一些新的少数样本。
SMOTE步骤__1.选一个正样本
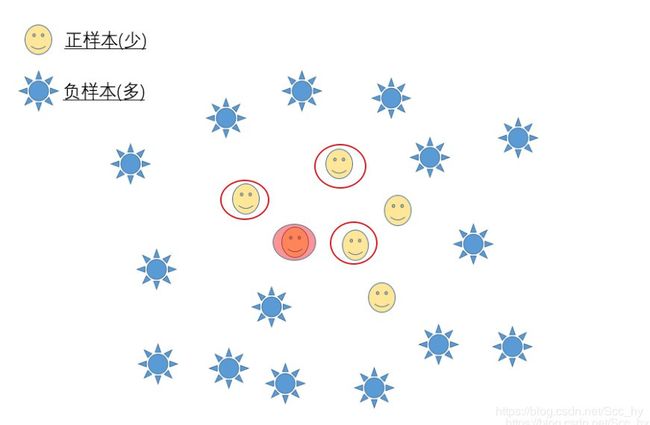
SMOTE步骤__2.找到该正样本的K个近邻(假设K = 3)
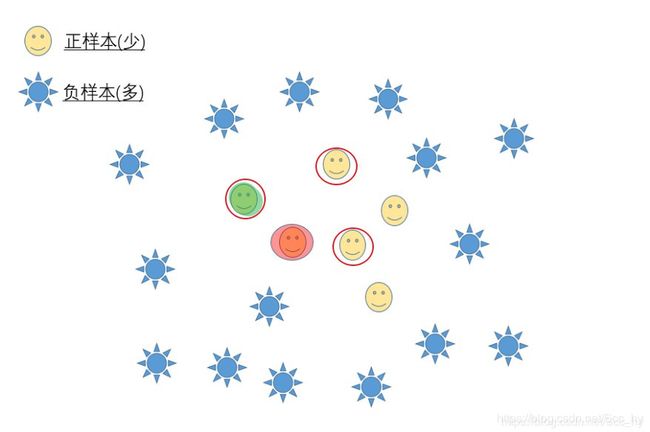
SMOTE步骤__3.随机从K个近邻中选出一个样本
SMOTE步骤__4.在正样本和随机选出的这个近邻之间的连线上,随机找一点。这个点就是人工合成的新正样本了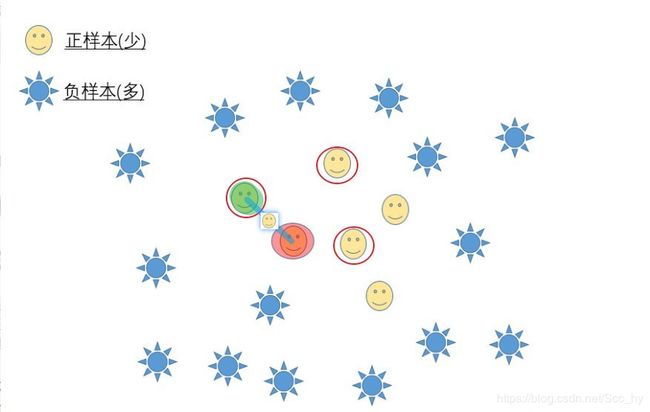
二、调包实现
2.1 R调包实现_SMOTE
- 主要参数解释:
-
perc.over = a需要生成的正样本:最后正样本数( 1 + a /100) * N:N为目前有的正样本数量
perc.under = a需要从负样本抽样的个数:最后负样本数(a / 100 * b / 10) * N
K = x用相近的x个样本(中的一个)生成正样本
library(DMwR)
# pos = (1 + perc.over/100) * N (N original pos sample)
# neg = (perc.over/100 * perc.under/100) * N
# SMOT oversample
newdata <- SMOTE(tp~., data_in
, perc.over = 300, k = 5, perc.under = 200
)
2.2 Python 调包实现_SMOTE
- imblearn.over_sampling.SMOTE(
-
sampling_strategy = ‘auto’,
random_state = None, ## 随机器设定
k_neighbors = 5, ## 用相近的5个样本(中的一个)生成正样本
m_neighbors = 10, ## 当使用kind={'borderline1', 'borderline2', 'svm'}
out_step = ‘0.5’, ## 当使用kind = 'svm'
kind = 'regular', ## 随机选取少数类的样本
–borderline1: 最近邻中的随机样本b与该少数类样本a来自于不同的类
–borderline2: 随机样本b可以是属于任何一个类的样本;
–svm:使用支持向量机分类器产生支持向量然后再生成新的少数类样本
svm_estimator = SVC(), ##svm分类器的选取
n_jobs = 1, ## 使用的例程数,为-1时使用全部CPU
ratio=None
)
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 42, n_jobs = -1)
x, y = sm.fit_sample(x_val, y_val)
仅用正样本的K近邻生成新正样本是正是SMOTE方法,考虑到(SMOTE的最终目的是分清正负样本的边界),所以需要对样本生成进行优化
2.2.1 SMOTE优化 borderline1 方法简述
Dgr = [] # 危险集
for i in 正样本:
1) 计算点 i 在训练集 D 上的 m 个最近邻。
x = i 的最近邻中属于负样本的数量
2) 如果 x = m,则 p 是一个噪声
next
3) 如果 0 ≤ x ≤ m/2, 则说明p很安全
next
4) 如果 m/2 ≤ x ≤ m, 那么点p就很危险了,我们需要在这个点附近生成一些新的少数类点
Dgr.append(x)
最后,对于每个在危险集(Dgr)中的点,使用SMOTE算法生成新的样本
2.2.2 SMOTE优化 borderline2 方法简述
前面1-4步骤均同 borderline1 方法
在最后进行SMOTE的时候:
采用了 比例分配 生成新样本
for i in Dgr:
1) 正样本 K 个近邻
2) 负样本 K 个近邻
3) 正样本 K 个近邻选取 alpha 比例的样本点
和 i 作随机的线性插值 ==>> 新正样本点
4) 负样本K个近邻选取 (1 - alpha) 比例的样本点
和 i 作随机的线性插值 ==>> 新正样本点
三、算法实现
#! /user/bin/python 3
# -*- coding: utf-8 -*-
# author: Scc_hy
# 2018-11-17
# SMOTE
from sklearn.neighbors import NearestNeighbors
import numpy as np
import pandas as pd
import copy
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
class TWO_SMOTE():
"""
不平二分类人工插值法采样
"""
def __init__(self,
K_neighbors = 5,
N_need = 200,
random_state = 42):
self.K_neighbors = K_neighbors
self.N_need = N_need
self.random_state = 42
def get_param_describe(self):
print(
"算法参数: \n"+
'K_neighbors: 和正样本相近的随机样本数' + "\n" +
"N_need: 需要增加的正样本数 (N_need // 100 * a)" + "\n" +
"random_state: 随机器设定" + "\n"
"\nover_sample 参数:\n" +
"x_data: 需要进行过采样的全部数据集(非文本DataFrame)" + "\n" +
"y_label: 类别标签(非文本DataFrame.Series)"+ "\n"
)
def div_data(self, x_data, y_label):
"""
将数据依据类分开
"""
tp = set(y_label)
tp_less = [a for a in tp if sum(y_label == a) < sum(y_label != a)][0]
data_less = x_data.iloc[y_label == tp_less, :]
data_more = x_data.iloc[y_label != tp_less, :]
tp.remove(tp_less)
return data_less, data_more, tp_less, list(tp)[0]
def get_SMOTE_sample(self, x_data, y_label):
"""
获取需要抽样的正样本
"""
sample = []
data_less, data_more, tp_less, tp_more = self.div_data(x_data, y_label)
n_integ = self.N_need // 100
data_add = copy.deepcopy(data_less)
if n_integ == 0 :
print('WARNING: PLEASE RE-ENTER N_need')
else:
for i in range(n_integ-1):
data_out = data_less.append(data_add)
data_out.reset_index(inplace = True, drop = True)
return data_out, tp_less
def over_sample(self, x_data, y_label):
"""
SMOTE算法简单实现
"""
sample, tp_less = self.get_SMOTE_sample(x_data, y_label)
knn = NearestNeighbors(n_neighbors = self.K_neighbors ,n_jobs = -1).fit(sample)
n_atters = x_data.shape[1]
label_out = copy.deepcopy(y_label)
new = pd.DataFrame(columns = x_data.columns)
for i in range(len(sample)): # 1. 选择一个正样本
# 2.选择少数类中最近的K个样本
k_sample_index = knn.kneighbors(np.array(sample.iloc[i, :]).reshape(1, -1),
n_neighbors = self.K_neighbors + 1,
return_distance = False)
# 计算插值样本
# 3.随机选取K中的一个样本
np.random.seed(self.random_state)
choice_all = k_sample_index.flatten()
choosed = np.random.choice(choice_all[choice_all != 0])
# 4. 在正样本和随机样本之间选出一个点
diff = sample.iloc[choosed,] - sample.iloc[i,]
gap = np.random.rand(1, n_atters)
new.loc[i] = [x for x in sample.iloc[i,] + gap.flatten() * diff]
label_out = np.r_[label_out, tp_less]
new_sample = pd.concat([x_data, new])
new_sample.reset_index(inplace = True, drop = True)
return new_sample, label_out
if __name__ == '__main__':
iris = load_iris()
irisdf = pd.DataFrame(data = iris.data, columns = iris.feature_names)
y_label = iris.target
# 生成不平二分类数据
iris_1 = irisdf.iloc[y_label == 1,]
iris_2 = irisdf.iloc[y_label == 2,]
iris_2imb = pd.concat([iris_1, iris_2.iloc[:10, :]])
label_2imb =np.r_[y_label[y_label == 1], y_label[y_label == 2][:10]]
iris_2imb.reset_index(inplace = True, drop = True)
smt = TWO_SMOTE()
x_new, y_new = smt.over_sample(iris_2imb, label_2imb)
以上就是SMOTE的简单实现,尚未有考虑到仅有 0 1变量,后期会更新