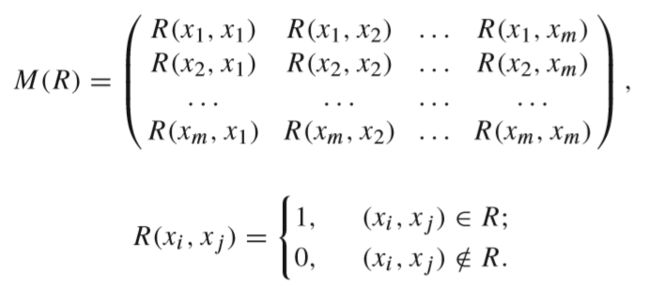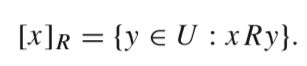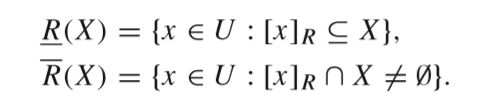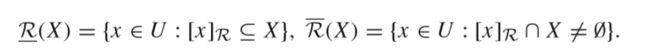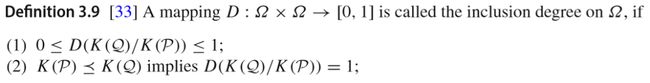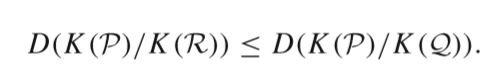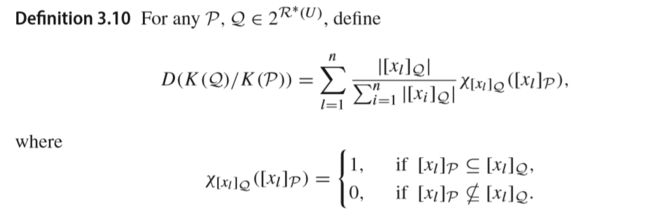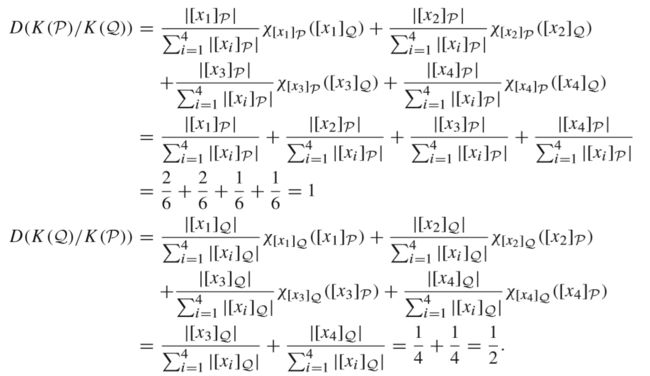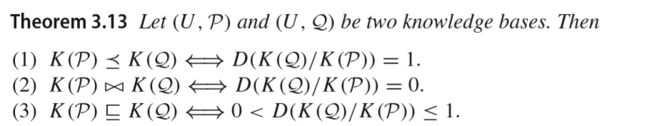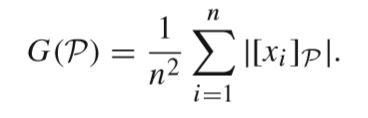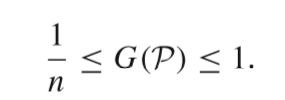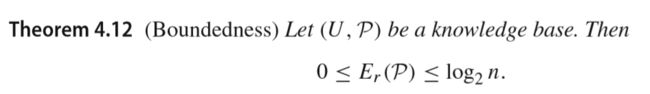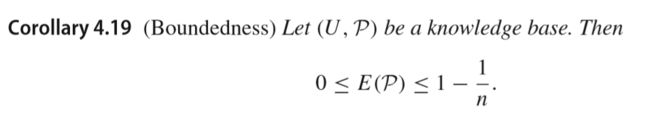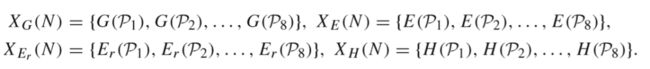论文浅尝 | 知识图谱的不确定性衡量

论文笔记整理：谭亦鸣，东南大学博士。

---

来源：Knowledge and Information Systems volume 62, pages611–637(2020)

链接：https://link.springer.com/article/10.1007/s10115-019-01363-0

概要

本文的核心工作是利用知识结构来衡量知识库的不确定性。文章的内容涵盖了以下几个部分：

1.首先队知识库的知识结构进行介绍；

2.以包含度特征为基础，提出知识结构与知识库之间的依赖以及独立性；

3.研究给定知识库的不确定性度量（并证明该度量方法是以知识库的知识结构为基础）；

4.最后，通过实验验证了本文方法的有效性，并从统计学的离散型和相关性两个方面做有效性分析。

动机与思路

作者用自问自答的形式对知识库不确定进行论述：

为何研究知识库不确定性的度量？因为知识库本身具有不确定性。

为何研究知识库的知识结构？因为知识结构有助于从知识库中发现知识。

为何使用知识结构衡量知识库的不确定性？因为很难对比给定知识库的不确定性值（原文是“This is because it is hard to compare the size of measure values of uncertainty for a given knowledge base.”，这句话没看明白，我的理解是：由于不同知识库的实体/关系规模差异较大，直接对知识库做不确定性衡量得到的量化结果不适合（不能够）反映出不同知识库之间的不确定性差异，因此要使用一个高层特征（知识结构），来代表并对不确定性的量化衡量做一个类似归一化的效果。），而且如果获取到两个知识结构之间的依赖关系，可以利用这个关系参与比较知识库之间的不确定性差异。

概念与定义

首先，作者使用矩阵M对于二元关系R进行了如下描述：

我们可以将矩阵中的x理解为知识库中的实体，R表明实体之间的关系，当R(x_i, x_j) =1时，表明x₁，x₂之间存在关系R.

可以看到，R在矩阵中可能构成三种关系场景（令实体集合为U，x, y∈U）：

1.xRx （Reflexive）

2.xRy且yRx（Symmetric）

3.xRy，yRz，且xRz（Transitive）

当R满足上述三种情况时，被称为“equivalence relation on U”,R∗(U)则代表所有equivalence relation on U”的集合的族（我理解为子集的集合）

对于一个equivalence relation R，通过以下公式，可以抽取实体集U在R上对应的类别子集：

因此，利用equivalence relation R可以对U进行类别划分，即：

故作者在这里提出定义：

2.1当R是U的一个equivalence relation，那么(U, R)被视作一个Pawlak近似空间（这里需要对粗糙集的概念做一个初步了解），在此基础上，X∈2^U（U的所有子集的族）的近似上下界可以通过以下公式定义：

2.2 当R∈2^R*(U)时（R*(U)指U上所有的equivalence relation的集合），(U, R)可以表示一个知识库，举个栗子来看：

可以看到这个知识库里有6个实体，4种关系，对应得到了四组矩阵。

因此对应可以得到知识库对应的近似空间的上下界：

知识结构定义：

对于一个知识库(U, R)，对于r∈R，可以通过以下公式描述r的知识结构：

因此整个知识库的知识结构为：

对于两个知识库(U, P)与(U, Q)，当：

则

知识结构之间的依赖性与独立性：

（参数在前文均已介绍过，这里不再赘述）

Inclusion degree（是一种衡量inclusion relationship质量的标准），以下定义给出了两个集合向量之间的Inclusion degree（3.9取值范围及定义，3.10计算方式）：

作者描述了一个计算inclusiondegree的例子：

1.首先给出两个知识库的知识结构：

2.计算inclusiondegree的过程为：

模型与算法

知识库粒度检测：

（首先给出粒度定义）

 

粒度的量化值如以下公式得到（作者在原文中对获取过程做了证明）：

并提出定理：

作者认为，知识粒化符合粒运算特征，并且从不同的层次重新定义了知识和信息。粒度测量值随类别增加而递减。缺陷在于无法区分粒度相似但结构不同的知识库。

知识库的熵检测：

（也是先给出了定义及知识熵的计算方式，可以看到这里的熵是完全基于知识结构的（定理4.8））

并且知识结构的关系与熵的关联性如下（原文附带了证明过程）：

这里还给出知识结构对应的粗糙熵定义及计算过程：

知识库的知识量（注意知识量是E，上面的粗糙熵是E_r）：

一些属性：

实验与结果

实验数据

为了验证上述测量方式对于知识库不确定性的量化衡量能力，作者在三个UCI数据集上进行了实验，数据集的统计信息如下表：

实验结果

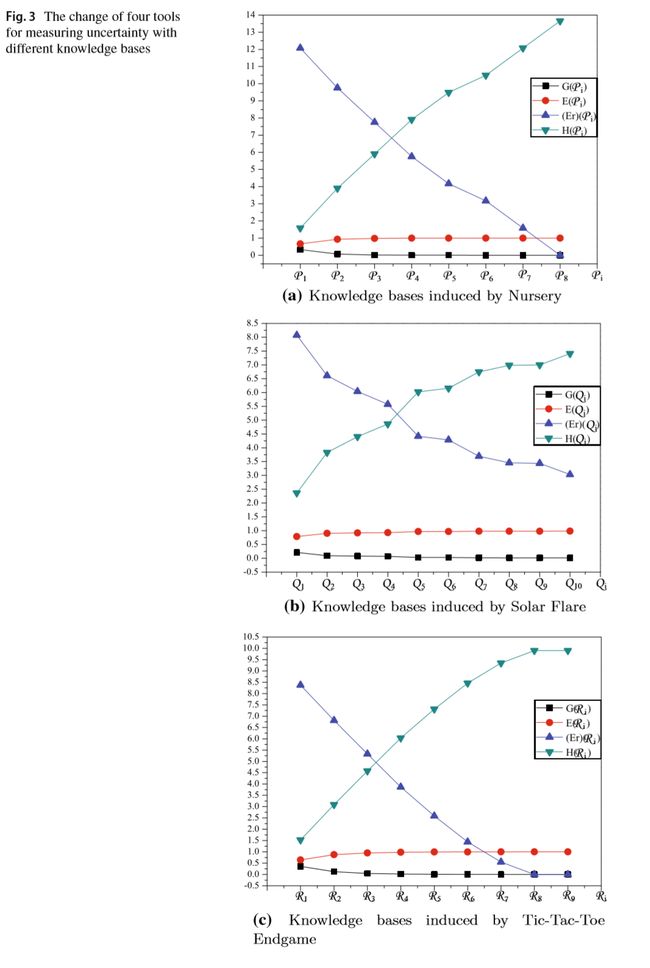
首先对于三个数据集，均获取到上一节介绍过的四种测量方式如下（以Nursery为例），|U|=12960，|A|=8，P_i=ind({a_i})(i = 1,2,…,8), P_i={P₁,P₂,…,P_i}(i = 1,2,…,8)：

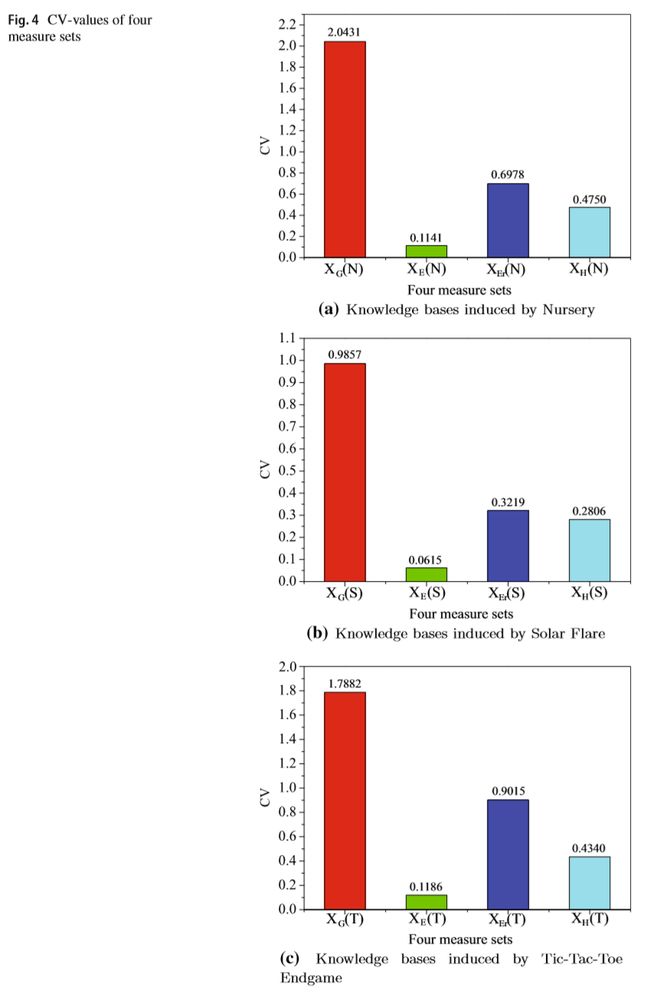
图3，4描述了这三种不同知识库（不同不确定性）的测量结果：

从各个指标的散度来看，知识量在衡量知识库不确定上表现出了更好的性能。

 

---

 

OpenKG

开放知识图谱（简称 OpenKG）旨在促进中文知识图谱数据的开放与互联，促进知识图谱和语义技术的普及和广泛应用。

点击阅读原文，进入 OpenKG 博客。