python基于scipy拟合构建所需统计分析模型,可视化分析展示
最近的工作中有一个需求就是,给我一批历史的数据,需要我基于统计分布模型来去拟合一下原始的数据,挖掘出来数据最有可能的统计分布是怎么样的,为后面的参数区间计算或者是概率值计算提供一个指导。
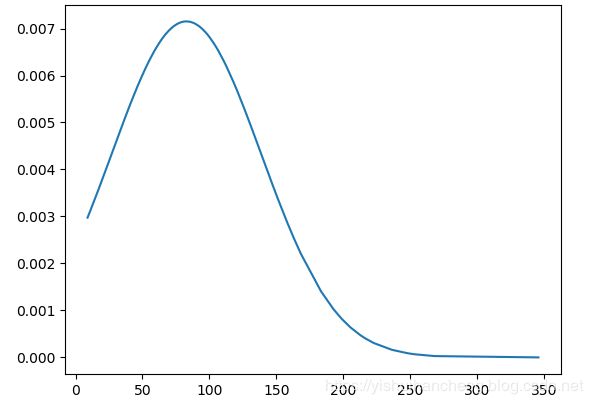
下面是我手中数据的概率分布情况:
从上面的概率分布函数曲线来看并不是一个正态分布的模型,所以我们就需要来去找别的统计模型来进行拟合分析了,标准模型比如:正态分布模型、F模型等都是为了简化实际中的计算出现的,基于上述的分布形状,这里基于scipy来寻找匹配性最好的模型。
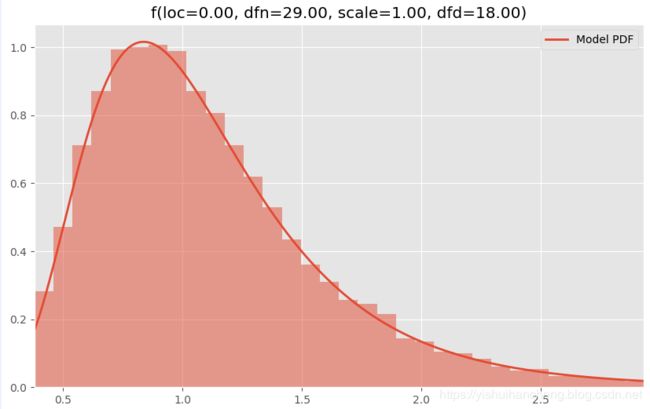
借助于自己残存的一点点统计模型知识,上述的数据分布与我印象中的F分布比较相似,这里先来看一下F分布:
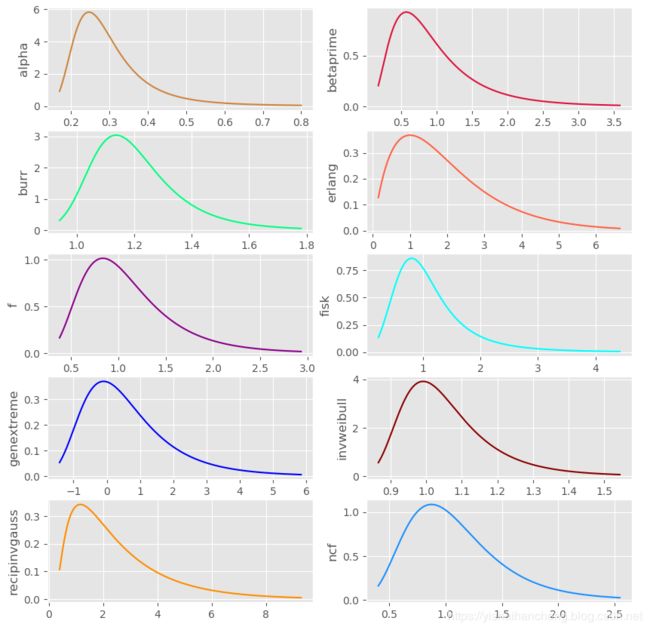
基于这个思路出发,我又找出来了几个相似的分布曲线,对比如下:
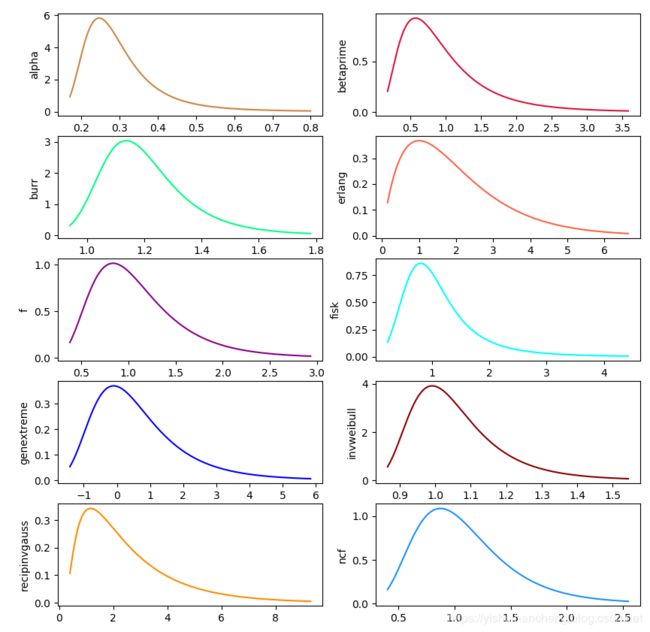
上面的这些图的绘图风格都是使用了R里面ggplot的风格,换成我自己平时的风格如下:
个人还是比较喜欢下面的这种风格的,更为简洁清爽。
具体的实现代码如下:
#!usr/bin/env python
# encoding:utf-8
from __future__ import division
"""
__Author__:沂水寒城
功能: 基于scipy构建所需分布模型,可视化展示
"""
import matplotlib
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
#绘图设置
#matplotlib.style.use('ggplot')
color_list=['#CD853F','#DC143C','#00FF7F','#FF6347','#8B008B','#00FFFF','#0000FF','#8B0000','#FF8C00',
'#1E90FF','#00FF00','#FFD700','#008080','#008B8B','#8A2BE2','#228B22','#FA8072','#808080']
size=1000
distribution1=stats.alpha(a=3.57, loc=0.0, scale=1.0)
distribution2=stats.betaprime(a=5, b=6, loc=0.0, scale=1.0)
distribution3=stats.burr(c=10.5, d=4.3, loc=0.0, scale=1.0)
distribution4=stats.erlang(a=2, loc=0.0, scale=1.0)
distribution5=stats.f(dfn=29, dfd=18, loc=0.0, scale=1.0)
distribution6=stats.fisk(c=3.09, loc=0.0, scale=1.0)
distribution7=stats.genextreme(c=-0.1, loc=0.0, scale=1.0)
distribution8=stats.invweibull(c=10.6, loc=0.0, scale=1.0)
distribution9=stats.recipinvgauss(mu=0.63, loc=0.0, scale=1.0)
distribution10=stats.ncf(dfn=27, dfd=27, nc=0.416, loc=0.0, scale=1.0)
#分布模型集合
distribution_list=[distribution1,distribution2,distribution3,distribution4,distribution5,
distribution6,distribution7,distribution8,distribution9,distribution10]
label_list=['alpha','betaprime','burr','erlang','f','fisk','genextreme','invweibull',
'recipinvgauss','ncf']
plt.clf()
plt.figure(figsize=(10,30))
for i in range(len(distribution_list)):
plt.subplot(5,2,i+1)
distribution=distribution_list[i]
model_data=distribution.rvs(size=size)
x = np.linspace(distribution.ppf(0.01), distribution.ppf(0.99), size)
y = distribution.pdf(x)
plt.plot(x,y,c=color_list[i])
plt.ylabel(label_list[i])
plt.show()
感兴趣的话可以拿去实验,接下来就是依照具体的分布曲线来去一一去匹配或者是拟合原始的数据了。当然这里也可以通过显著性检验的形式来去做,在我之前的博客里面也有相关的说明和实现,感兴趣的话可以去看看。