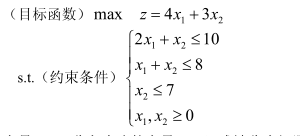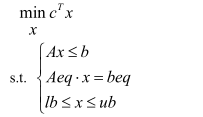【数学建模】线性规划

1.线性规划简介

线性规划（LP）是数学规划的一个分支。

x1,x2为决策变量，约束条件记为s.t.（subject to）。

2.线性规划的matlab标准形式

线性规划的目标函数可以求最大值也可以求最小值，约束条件的不等号可以是小于号也可以是大于号，因此在matlab中给出了统一形式。

其中c和x均为n维列向量，A、Aeq为适当维数（列数与x维数相同，行数与约束条件数相同）,b、beq为适当维数的列向量（维数与约束条件数相同）。

例如：
max  cTx  s.t.   Ax≥b  m a x     c T x     s . t .       A x ≥ b  

matlab中为：
min  −cTx  s.t.   −Ax≤b  m i n     − c T x     s . t .       − A x ≤ b  

3.线性规划中解的概念

可行解：满足约束条件的 解x = （x1,x2…xn），称为线性规划问题的可行解，从而使目标函数达到最大值或者最小值的可行解称为最优解。
可行域：所有可行解构成的集合称为问题的可行域，记为R。

4.一般的线性规划问题

在一般的n维空间中，满足 ∑ni=1aixi = b ∑ i = 1 n a i x i   =   b 的点集称为一个超平面，而满足 ∑ni=1aixi ≥ b ∑ i = 1 n a i x i   ≥   b （或者 ∑ni=1aixi ≤ b ∑ i = 1 n a i x i   ≤   b ）的点集称为一个半平面，若干个半平面的交集称为多胞形，有界的多胞形称为多面体。因此线性规划的可行域必定为多胞形（空集也视为多胞形）。若该区域R为凸集，则凸集中的任意两点的连线必然在该凸集中，若x为区域R的极点，则x不能位于R中的任意两点的连线上。

5.matlab中线性规划求解过程

① 利用linprog函数返回最小值解向量。
② value = c’ * x求最小值。

基本函数形式是 linprog(c,A,b) , c用于确定等值线（列向量），返回值为向量x。
其他的函数形式：
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,x0,OPTIONS)
x0为向量x的初始值，一般使用zeros()函数 初始化，LB和UB分别是向量x的下界向量和上界向量。返回值为fval（目标函数c’ * x的值）。

6.常见技巧

问题为：

min|x1|+|x2|+…+|xn|  s.t.  Ax≤b  min | x 1 | + | x 2 | + … + | x n |     s . t .     A x ≤ b  
事实上，对于任意的 xi x i ，存在 ui,vi u i , v i 满足：
xi=ui−vi  ,  |xi|=ui+vi x i = u i − v i     ,     | x i | = u i + v i
令 ui=(xi+|xi|2),vi=(|xi|−xi2) u i = ( x i + | x i | 2 ) , v i = ( | x i | − x i 2 ) 即可满足。

转换为：
min  ∑ni=1(ui+vi) m i n     ∑ i = 1 n ( u i + v i )
s.t.{A(ui−vi)≤b,u,v≥0, s . t . { A ( u i − v i ) ≤ b , u , v ≥ 0 ,

7.运输问题（产销平衡）

8.指派问题

1.数学模型

2.利用匈牙利算法
算法主要思想：如果系数矩阵中C=( cij c i j )一行（或一列）中每一个元素都加上或减去同一个数，得到新矩阵B，则以B或C为系数矩阵的指派问题具有相同的最优指派。
最优指派的结果是一个2行n列的行列式，第一行为第i人，第二行为被指派的地点。
求解中心：变换出n个不同行不同列的零元素。