hdu1086 You can Solve a Geometry Problem too(判断线段相交)
hdu1086 You can Solve a Geometry Problem too(判断线段相交)
题目
描述
Many geometry(几何)problems were designed in the ACM/ICPC. And now, I also prepare a geometry problem for this final exam. According to the experience of many ACMers, geometry problems are always much trouble, but this problem is very easy, after all we are now attending an exam, not a contest
Give you N (1<=N<=100) segments(线段), please output the number of all intersections(交点). You should count repeatedly if M (M>2) segments intersect at the same point.
Note:
You can assume that two segments would not intersect at more than one point.
输入
Input contains multiple test cases. Each test case contains a integer N (1=N<=100) in a line first, and then N lines follow. Each line describes one segment with four float values x1, y1, x2, y2 which are coordinates of the segment’s ending.
A test case starting with 0 terminates the input and this test case is not to be processed.
输出
For each case, print the number of intersections, and one line one case.
输入样例 1
2
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.00
3
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.00
0.00 0.00 1.00 0.00
0
题意:输入n段线段的两个端点,问我们这些线段组之间有多少个交点。
向量叉乘
首先我们应该想思考线段相交的话需要满足什么条件?在此之前我先来说一下什么是向量叉乘
定义:向量积(cross product),数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛,通常应用于物理学光学和计算机图形学中。
公式:a=(X1,Y1,Z1), b=(X2,Y2,Z2),
a×b=(Y1Z2-Y2Z1,Z1X2-Z2X1,X1Y2-X2Y1)
上面的公式是在三维空间里的叉乘公式,而转化成二维的话,我们只需要令Z1=Z2=0就可以,即:
a=(X1,Y1) b=(X2,Y2) a×b=(X1Y2-X2Y1)
说到这里或许大家还会有疑问,向量叉乘和这道题又有什么关系呢?别急,马上进入主题
跨立实验
如果两线段相交,则两线段必然相互跨立对方.若P1P2跨立Q1Q2 ,则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧,即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0.上式可改写成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) 0.当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时,说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线,但是因为已经通过快速排斥试验,所以 P1 一定在线段 Q1Q2上;同理,( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2上.所以判断P1P2跨立Q1Q2的依据是:( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) = 0.同理判断Q1Q2跨立P1P2的依据是:( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) = 0。
看了上面这段话是不是还有点懵?简单来说就是如果向量a在向量b的左侧(b的逆时针方向),那么a×b<0,如果向量a在向量b的右侧(b的顺时针方向),那么a×b>0,说到这里是不是已经有点想法了?
图解
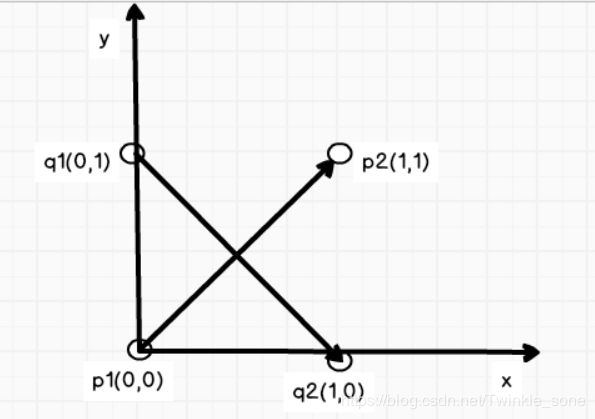
如例1的4个点:
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.00
在坐标轴上画出,如下图:
然后用上面的跨立实验来判定这两段线段是否相交
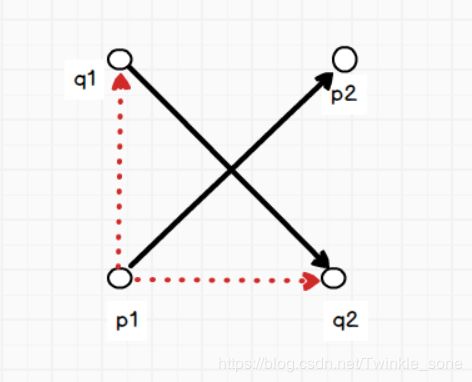
(1)先以向量p1p2为主,判断向量q1q2是否跨立p1p2
(2)求出所需向量的值,我们需要的有p1p2,p1q1,p1q2
p1p2 = (1,1) p1q1 = (0,1) p1q2 = (1,0)
套用公式 a×b=(X1Y2-X2Y1)
p1p2 × p1q1 = 1 p1p2 × p1q2 = -1
所以可以得出p1q1和p1q2分别位于p1p2的两侧,所以两线段就一定相交了吗?
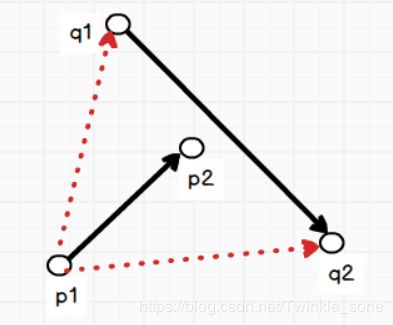
我们再来看看这种情况:
这种情况p1q1和p1q2分别位于p1p2的两侧,可是它们之间却没有交点,所以在网上很多的题解中都会提到一个快速排斥试验,即:设以线段 P1P2 为对角线的矩形为R,设以线段 Q1Q2 为对角线的矩形为T,如果R和T不相交,显然两线段不会相交。
但是方法是很多的,我们也可以不去进行快速排斥实验,我们只需要以向量q1q2为主再将我们的步骤重复一次就可以了。
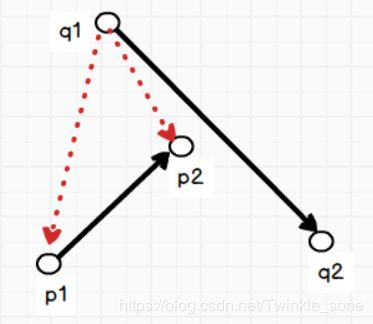
从图中便可以看出向量q1p2和q1p1均位于q1q2的右边(顺时针方向)所以他们不相交。
AC代码
#include
#include
using namespace std;
struct Line{
double x1,x2,y1,y2;
}l[100];
int judge(Line l1,Line l2){
double qp1[2],qp[2],qq[2],pq1[2],pq[2],pp[2];
qq[0] = l1.x2-l1.x1;
qq[1] = l1.y2-l1.y1;
pq[0] = l2.x1-l1.x1;
pq[1] = l2.y1-l1.y1;
pq1[0] = l2.x2-l1.x1;
pq1[1] = l2.y2-l1.y1;
pp[0] = l2.x2-l2.x1;
pp[1] = l2.y2-l2.y1;
qp[0] = l1.x1-l2.x1;
qp[1] = l1.y1-l2.y1;
qp1[0] = l1.x2-l2.x1;
qp1[1] = l1.y2-l2.y1;
if((pq[0]*qq[1]-pq[1]*qq[0])*(pq1[0]*qq[1]-pq1[1]*qq[0]) <= 0)
if((qp[0]*pp[1]-qp[1]*pp[0])*(qp1[0]*pp[1]-qp1[1]*pp[0]) <= 0)
return 1;
return 0;
}
int main(){
int n,i,j;
while(scanf("%d",&n)&&n){
int sum = 0;
for(i=0;i