Redis跳跃表实现原理(加快在有序链表中的查找速度)

Redis跳跃表实现原理

我们知道二叉搜索算法能够高效的查询数据，但是需要一块连续的内存，而且增删改效率很低。
跳表，是基于链表实现的一种类似“二分”的算法。它可以快速的实现增，删，改，查操作。
我们先来看一下单向链表如何实现查找

当我们要在该单链表中查找某个数据的时候需要的时间复杂度为O(n).
怎么提高查询效率呢？如果我们给该单链表加一级索引，将会改善查询效率。

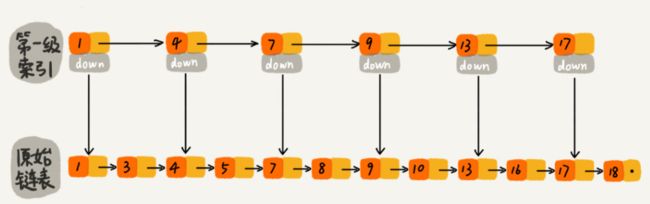
如图所示，当我们每隔一个节点就提取出来一个元素到上一层，把这一层称作索引，其中的down指针指向原始链表。

当我们查找元素16的时候，单链表需要比较10次，而加过索引的两级链表只需要比较7次。当数据量增大到一定程度的时候，效率将会有显著的提升。

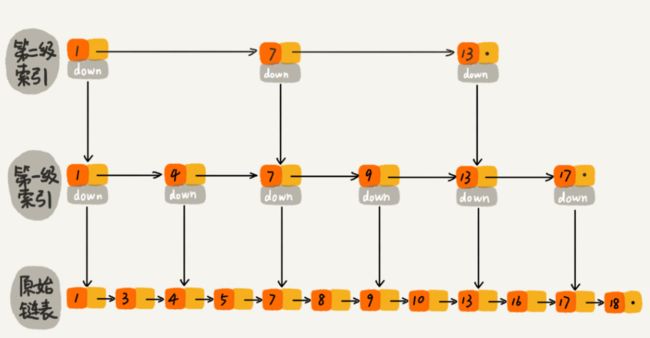
如果我们再加多几级索引的话，效率将会进一步提升。这种链表加多级索引的结构，就叫做跳表。

跳表的查询时间复杂度可以达到O(logn)

 

 

高效的动态插入和删除

跳表也可以实现高效的动态更新，定位到要插入或者删除数据的位置需要的时间复杂度为O(logn).
在插入的时候，我们需要考虑将要插入的数据也插入到索引中去。在这里使用的策略是通过随机函数生成一个随机数K,然后将要插入的数据同时插入到k级以下的每级索引中。

一般来说，如果要做到严格 O(logn) ，上层结点个数应是下层结点个数的 1/2 。但是这样实现会把代码变得十分复杂，就失去了它在 OI 中使用的意义。

此外，我们在实现时，一般在插入时就确定数值的层数，而且层数不能简单的用随机数，而是以1/2的概率增加层数。

用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布，K 的期望值 E[K] = 1/p = 2. 就是说，各个元素的层数，期望值是 2 层。

同时，为了防止出现极端情况，设计一个最大层数MAX_LEVEL。c语言中如果使用非指针版，定义这样一个常量会方便许多，更能节省空间。如果是指针版，可以不加限制地任由它增长。

 

跳表具有如下性质：

(1) 由很多层结构组成

(2) 每一层都是一个有序的链表

(3) 最底层(Level 1)的链表包含所有元素

(4) 如果一个元素出现在 Level i 的链表中，则它在 Level i 之下的链表也都会出现。

(5) 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

 

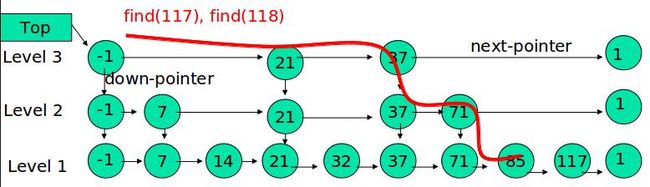
查找

从最上层开始，如果key小于或等于当层后继节点的key,则平移一位；如果key更大，则层数减1，继续比较。最终一定会到第一层。

 

插入

先确定该元素要占据的层数 K（采用丢硬币的方式，这完全是随机的）。

然后在 Level 1 ... Level K 各个层的链表都插入元素。

用Update数组记录插入位置，同样从顶层开始，逐层找到每层需要插入的位置，再生成层数并插入。

例子：插入 119， K = 2

 

如果 K 大于链表的层数，则要添加新的层。

例子：插入 119， K = 4

 

 

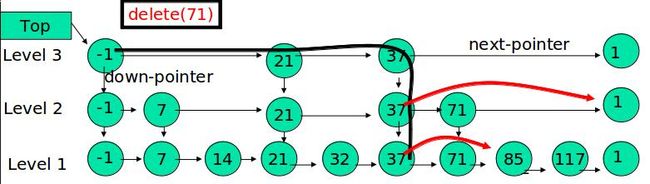
跳表的删除

在各个层中找到包含 x 的节点，使用标准的 delete from list 方法删除该节点。

例子：删除 71

 

redis基本数据结构之ZSet

ZSet数据结构类似于Set结构，只是ZSet结构中，每个元素都会有一个分值，然后所有元素按照分值的大小进行排列，相当于是一个进行了排序的链表。

如果ZSet是一个链表，而且内部元素是有序的，在进行元素插入和删除，以及查询的时候，就必须要遍历链表才行，时间复杂度就达到了O(n),这个在以单线程处理的Redis中是不能接受的。所以ZSet采用了一种跳跃表的实现。

这种跳跃表的实现，其实和二分查找的思路有点接近，只是一方面因为二分查找只能适用于数组，而无法适用于链表，所以为了让链表有二分查找类似的效率，就以空间换时间来达到目的。

跳跃表因为是一个根据分数权重进行排序的列表，可以再很多场景中进行应用，比如排行榜，搜索排序等等。

跳跃表的实现

Redis的跳跃表由redis.h/zskiplistNode和redis.h/zskiplist两个结构定义，其中zskiplistNode结构用于表示跳跃表节点，而zskiplist结构则用于保存跳跃表节点的相关信息，比如节点的数量，以及指向表头节点和表尾节点的指针等等。

上图展示了一个跳跃表示例，位于图片最左边的是zskiplist结构，该结构包含以下属性：

header：指向跳跃表的表头节点
tail：指向跳跃表的表尾节点
level：记录目前跳跃表内，层数最大的那个节点的层数(表头节点的层数不计算在内)
length：记录跳跃表的长度，也即是，跳跃表目前包含节点的数量(表头节点不计算在内)

 

位于zskiplist结构右方的是四个zskiplistNode结构，该结构包含以下属性：

层(level)：节点中用L1、L2、L3等字样标记节点的各个层，L1代表第一层，L2代表第二层，依次类推。每个层都带有两个属性：前进指针和跨度。前进指针用于访问位于表尾方向的其他节点，而跨度则记录了前进指针所指向节点和当前节点的距离。在上面的图片中，连线上带有数字的箭头就代表前进指针，而那个数字就是跨度。当程序从表头向表尾进行遍历时，访问会沿着层的前进指针进行。

后退(backward)指针：节点中用BW字样标记节点的后退指针，它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。

分值(score)：各个节点中的1.0、2.0和3.0是节点所保存的分值。在跳跃表中，节点按各自所保存的分值从小到大排列。

成员对象(obj)：各个节点中的o1、o2和o3是节点所保存的成员对象。

 

注意表头节点和其他节点的构造是一样的：表头节点也有后退指针、分值和成员对象，不过表头节点的这些属性都不会被用到，所以图中省略了这些部分，只显示了表头节点的各个层。

 

命令操作

添加元素，zadd zsetName score1 value1 score2 value2 score3 value3 .....

查看所有元素，zrange zsetName 0 -1

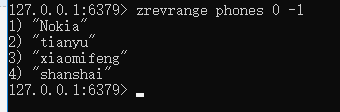
查看所有元素，按score逆序排列， zrevrange zsetName 0 -1

元素数量，zcard zsetName

获取指定value的分数， zscore zsetName value

获取指定value的排名，zrank zsetName value(从0开始)

获取指定分值区间中的元素， zrangebyscore zsetName scoreStart scoreEnd(包含上下区间)（注意inf表示无穷大，-inf表示服务券大）

获取指定分值区间中的元素，并且返回分数， zrangebyscore zsetName scoreStart scoreEnd withscores

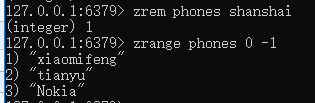
删除元素，zrem zsetName value

 

 

跳表实现代码(Java)

package cc.wsyw126.java.algorithm;

/**
 * @author yangjunpeng
 * @version $Id: SkipList.java, v 0.1 2020年04月18日 下午10:09 yangjunpeng Exp $
 */
import java.util.Random;

public class SkipList {
    private static final int MAX_LEVEL  = 16;
    private int              levelCount = 1;
    private Node             head       = new Node();
    private Random           random     = new Random();

    /**
     * 查找value
     *
     * @param value
     * @return
     */
    public Node find(int value) {
        Node p = head;
        //下沉一个层次
        for (int i = levelCount - 1; i >= 0; i--) {
            //如果同层次下一个节点的值大于要找的值，则下沉一层。反之：同层次往后遍历。
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
        }
        //find
        if (p.forwards[0] != null && p.forwards[0].data == value) {
            return p.forwards[0];
        }

        return null;
    }

    /**
     * 构建跳表，插入value
     *
     * @param value
     */
    public void insert(int value) {
        Node p = head;
        int level = randomLevel();
        Node node = new Node();
        node.data = value;
        node.maxLevel = level;
        // 用update数组记录插入位。
        // 例子：a.forwards[i]指向b。
        // 开始时状态：a->b，此时记录下a，后面for循环会将这里改为a->value->b。
        Node[] update = new Node[level];
        for (int i = level - 1; i >= 0; i--) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            //用update数组记录插入位。
            update[i] = p;
        }
        //for循环会将value，插入到待插入的位置：a->b改为a->value->b。
        for (int i = 0; i < level; i++) {
            node.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = node;
        }
        //如果新的层次更高，那么就更新。
        if (levelCount < level) {
            levelCount = level;
        }

    }

    /**
     * 删除value
     *
     *
     * @param value
     */
    public void delete(int value) {
        Node[] deleteNode = new Node[MAX_LEVEL];
        Node p = head;
        //同insert
        for (int i = levelCount - 1; i >= 0; i--) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            deleteNode[i] = p;
        }
        //存在value对应的节点
        if (p.forwards[0] != null && p.forwards[0].data == value) {
            //for循环会将value删除。a->value->b修改为：a->b。
            for (int i = levelCount - 1; i >= 0; i--) {
                if (deleteNode[i] != null && deleteNode[i].forwards[i] != null
                    && deleteNode[i].forwards[i].data == value) {
                    deleteNode[i].forwards[i] = deleteNode[i].forwards[i].forwards[i];
                }
            }
        }
    }

    /**
     * 顺序输出链表中的数据
     */
    public void printAll() {
        Node p = head;
        while (p.forwards[0] != null) {
            System.out.print(p.forwards[0] + " ");
            p = p.forwards[0];
        }
        System.out.println();
    }

    /**
     * 随机生成层次
     * 用实验中丢硬币的次数 K 作为元素占有的层数。
     * 显然随机变量 K 满足参数为 p = 1/2 的几何分布，K 的期望值 E[K] = 1/p = 2.
     * 就是说，各个元素的层数，期望值是 2 层。
     *
     * @return
     */
    private int randomLevel() {
        int level = 0;
        for (int i = 0; i < MAX_LEVEL; i++) {
            if (random.nextInt() % 2 == 1) {
                level++;
            }
        }
        return level;
    }

    class Node {
        /** 存放数据 */
        private int    data;
        /** forwards[i] 表示这个结点在第 i 层的下一个结点编号。*/
        private Node[] forwards = new Node[MAX_LEVEL];
        /** 该节点最高层次 */
        private int    maxLevel;

        public String toString() {
            StringBuilder sb = new StringBuilder();
            sb.append("{data: ");
            sb.append(data);
            sb.append("; level: ");
            sb.append(maxLevel);
            sb.append(" }");
            return sb.toString();
        }
    }

    public static void main(String[] args) {
        SkipList skipList = new SkipList();
        for (int i = 0; i < 5; i++) {
            skipList.insert(i);
        }

        int value = 16;
        Node node = skipList.find(value);
        System.out.println("node = " + node);

        skipList.printAll();

        skipList.delete(value);
        skipList.printAll();
        node = skipList.find(value);
        System.out.println("node = " + node);
    }

}

Docker 安装 Redis：

https://www.runoob.com/docker/docker-install-redis.html

 

参考资料：
https://www.jianshu.com/p/43039adeb122
https://blog.csdn.net/belalds/article/details/93876483
https://blog.csdn.net/u010694337/article/details/52550593
https://www.cnblogs.com/wuyizuokan/p/11108417.html
备注：
转载请注明出处：https://blog.csdn.net/WSYW126/article/details/105611088
作者：WSYW126