投影与三维视觉
- 投影与三维视觉
- 一 投影
- 二 仿射变换和透视变换
- 2.1 POSIT:3D姿态估计
- 2.2 立体成像
- 三 三角测量
- 四 对极几何
- 五 本征矩阵和基础矩阵
- 5.1**极线的计算**
- 六 立体标定
- 七 立体校正
- 八 校正映射
- 九 立体匹配
- 十 从三维重投影获得深度映射
投影与三维视觉
一般情况下,没有可靠的方法可以做到不依赖多幅图像就可以进行标定或提取3D信息。利用多幅图像重建三维场景的最常见情形就是立体视觉。在立体视觉中,同时在不同位置上拍摄两幅图像(或者更多)中的特征,然后对图像中的相应特征进行匹配,分析其中的差异,从而获得深度信息。
另一个情形是从运动中得到结构。这种情况下,我们可能只用一个摄像机,但是要在不同时间从不同的地方拍摄多幅图像。对前者而言,我们主要对视差效应(三角部分)感兴趣,并作为计算距离的一种方法;而后者,则是通过计算基础矩阵(将两个不同场景联系到一起)来获得场景理解的数据源。
一 投影
一旦对摄像机完成了标定(见我的上一篇博客《摄像机模型与标定》),就有能将现实物理世界中的点无歧义地投影到图像上。这意味着给定对于摄像机三维物理坐标框架下的位置,我们就可以计算该三维点在成像仪中的坐标,即像素坐标。在OpenCV中,这个转换过程通过函数cvProjectPoints2()来实现的。
可以通过如下案列来更好地理解该函数的用法(在高版本的OpenCV中函数名变为了projcetPoints()):
void project2Ellipse(double &radius, double &Rx, double &Ry, double &Rz, double &Tz, int &sigma, vector(in_pnts[i].y, in_pnts[i].x) = 200;
}
else
{
srcImg.at(in_pnts[i].y, in_pnts[i].x) = 50;
}
}
}
注:上面的代码可以 参考我之前的一篇名为:《罗德里格斯》的博文,以便更好地理解其含义。
二 仿射变换和透视变换
仿射变换可以将矩形映射为任意平行四边形;而更一般的情形是,透视变换将矩形映射为任意四边形。
透视变换与透视投影关系密切。透视投影是使用中心投影法,沿着一系列最终汇聚到一个被称为投影中心的点的投影线,将三维物理世界中的点投影变换到二维图像平面中。
2.1 POSIT:3D姿态估计
在进入立体视觉之前,我们首先了解一下一个能够估计已知物体三维位置的算法,即POSIT算法。POSIT(英文“Pose from Orthography and Scaling with iteration”的缩写)是1992年首次提出的用于计算3D物体(其精确的维数是已知的)的姿态的一种算法(位置T和方向R由6个参数描述)。为了计算这个姿态,必须找到物体表面的至少4个非共面点在相应二维图像上的位置。
由正交投影和尺寸变换提取姿态(POS),并假设物体上的点具有相同的有效深度而且原始模型的大小变化只与其距摄像机的远近比例相关。在这种情况下,基于尺度变换的物体三维姿态的解是闭合式的。所有物体点都具有相同有效深度的假设意味着物体距离摄像机足够远,使得我们可以忽略了各个点在物体内部的深度差异,这个假设称为”弱透视近似”。
2.2 立体成像
在实际应用中,两台摄像机的立体成像过程包括以下四个步骤。
1)消除畸变:使用数学方法消除径向和切线方向上的镜头畸变,在这一步输出的是无畸变图像。
2)摄像机校正:调整摄像机间的角度和距离,输出行对准的校正图像。
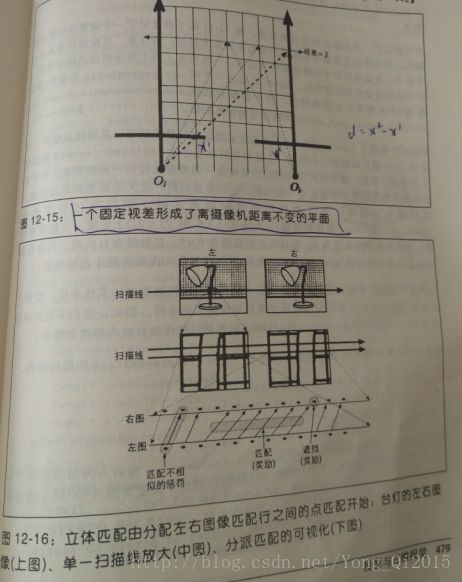
3)图像匹配:查找左右摄像机视场中的相同特征。这一步输出的是视差图,差值是指左右图像上的相同特征在x坐标上的差值x1-Xr。
4)重投影:当知道了摄像机的相对几何位置后,就可以将视差图通过三角测量的方法转成距离。本步骤输出等深度图。
我们先从最后一步说起,然后分析前三步。
三 三角测量
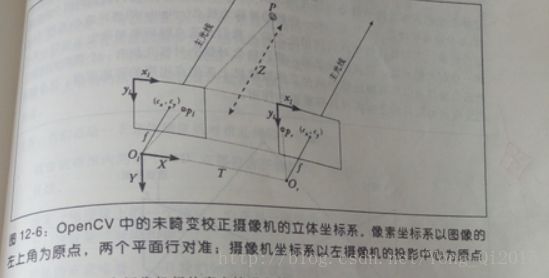
假设我们已有一套无畸变、对准、已测量好的完美标准立体实验台,如图所示:
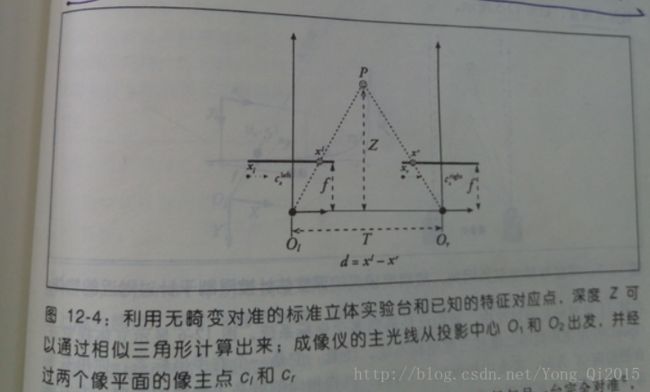
两台摄像机的像平面精确位于同一平面上,光轴严格平行(光轴是从投影中心o朝向主点c方向引出的一条射线,也称为主光线),距离一定,焦距相同fl=fr。并且假设主点
Cx和Cy已经校准,在左右图像上具有相同的像素坐标。
注意:
不要将主点和图像中心混为一谈,主点是主光线与像平面的交点,该交点在镜头的光轴上。像平面很少与镜头完美地重叠,因此图像中心也几乎不会和像主点重合。
进一步假设两幅图像是行对准的,并且一台摄像机的像素行与另一台完全对准,我们称为摄像机前向平行排列。再假设物理世界中的点P在左右图像上的成像点为Pl
和Pr,相应的横坐标分别为xl和xr。
在这个简单化的例子中,xl和xr分别表示点在左右成像仪上的水平位置,这使得深度与视差成反比例关系,视差简单的定义为
如图12-4所示,利用相似三角形可以很容易推导出Z值。由图可知:
因为深度与视差成反比,二者有明显的非线性关系。
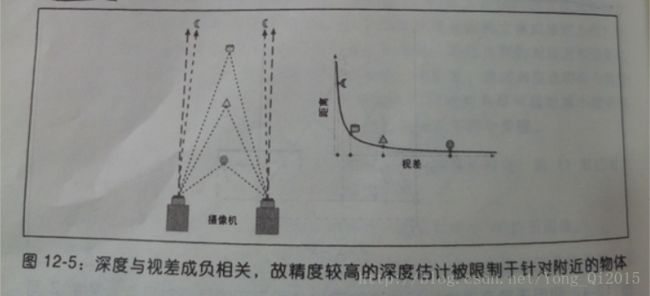
当视差接近于0时,微小的视差变化会导致很大的深度变化;当视差较大时,微小的视差变化几乎不会引起深度多大的改变。结果就是,立体视觉系统仅仅对于物体与摄像机相距较近时具有较高的深度精度。
现在我们必须花一些精力去弄明白,怎么样才能现实世界中摄像机设备映射到理想安排的几何状态。在真实世界中,摄像机几乎不可能会像图12-4那样的严格的前向平行对准。不过,我们可以通过数学的方法计算投影图和畸变图,从而将左右图像校正成为前向平行对准。在设计立体实验台的时候,最好近似地将摄像机放置成前向对准,并尽量让摄像机水平对准。
四 对极几何
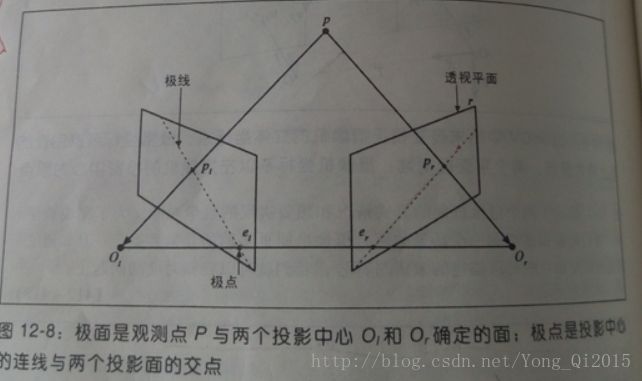
立体成像的基本几何学就是对极几何。从本质上来说,对极几何就是将两个针孔模型(每个摄像机就是一个针孔)和一些新的被称为极点的感兴趣点结合起来。
我们总结一下立体摄像机对极几何的一些事实。
摄像机视图内的每个3D点都包含在极面内,极面与每幅图像相交的直线是极线。
给定一幅图像上的一个特征,它在另一幅图像上的匹配视图一定在对应的极线上。这就是”对极约束”.
对极约束意味着,一旦我们知道立体试验台的对极几何之后,对两幅图像间匹配特征的二维搜索就转变成了沿着极线的一维搜索。这不仅仅节省了大量的计算,还允许我们排除许多导致虚假匹配的点。
次序是保留的。如果两个点A和B在两幅成像仪上都可见,按顺序水平出现在其中成像仪上,那么在另一个成像仪上也是水平出现。
五 本征矩阵和基础矩阵
你可能急着想知道计算极线的OpenCV函数了。但在介绍这些函数之前,我们实际上还需要两个因素。这两个因素就是本征矩阵E和基础矩阵F。矩阵E包含在物理空间中两个摄像机相关的旋转和平移信息,矩阵F除了包含E的信息外还包含了两个摄像机的内参数。由于F包含了这些内参数,因此它可以在像素坐标系将两台摄像机关联起来。
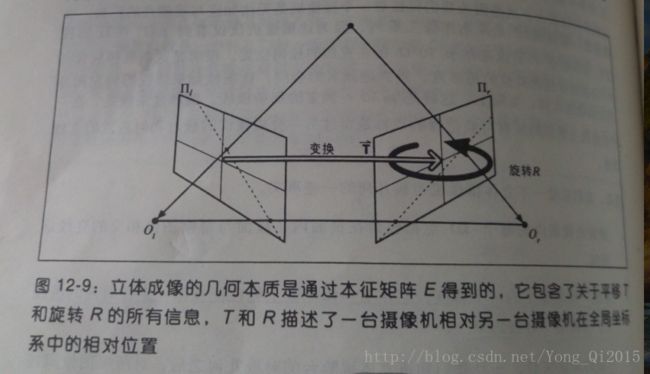
我们再补充一下E和F的区别:
1)本征矩阵E联系的是物理坐标系下的点;
2)基础矩阵F联系的是像平面上的点。
5.1**极线的计算**
一旦有了基础矩阵,我们就能够计算极线。OpenCV中cvComputeCorrespondEpilines()函数根据一幅图像中的点列,计算其在另一幅图像中对应的极线。注意,给定一幅图像上的任意一点,在另外一幅图像上总有对应的极线。每条计算的极线以三点(a,b,c)的形式编码,这样极线就定义如下:
为了算出这些极线,函数需要前面用cvFindFundamentalMat()算出的基础矩阵。
六 立体标定
立体标定是计算空间上两台摄像机几何关系的过程。相反地,立体校正则是对个体图像进行纠正的过程,这样保证这些图像可以从像平面行对准的两幅图像获得。通过这样的校正,两台摄像机的光轴(或者主光线)就是平行的,即所谓无穷远处相交。
七 立体校正
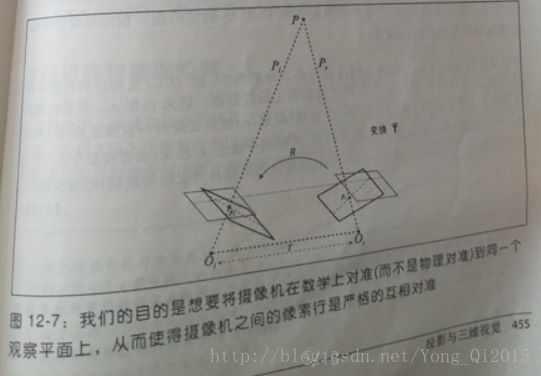
当两个像平面是完全的行对准时(见图12-4),计算立体视差是最简单的。不幸的是,如前面所讨论的,由于两台摄像机几乎不可能有准确的共面和行对准的成像平面,完美的对准结构在真实的立体系统中几乎不存在。图12-7显示了立体校正的目的:我们要对两台摄像机的图像平面重投影,使得它们精确落在同一个平面上,而且图像的行完全地对准到前向平行的结构上。如何选择特定的平面使摄像机保持数学对准依赖于所使用的算法。
有很多算法可以计算我们的校正项,OpenCV实现了其中的两种:一是Hartley算法,它只使用基础矩阵来生成非标定立体视觉;二是Bouguet算法,它使用两台标定摄像机的旋转和平移参数。
八 校正映射

一旦有了立体标定项,我们就可以单独调用cvInitUndistortRectifyMap()来事先计算左右视图的校正查找映射表。对任何图像到图像的映射函数,由于目标位置是浮点型的缘故,正向映射(即根据原始图像上的点计算其到目标图像上的点),不会命中目标图像对应的像素位置,因为目标图像看起来像瑞士硬干酪。因此我们采用逆向映射。
这个校正的过程如图12-11所示。图中公式流程图就是真实的从(c)到(a)的向后校正过程,称为逆向映射。
九 立体匹配
立体匹配——匹配两个不同的摄像机视图的3D点——只有在两摄像机的重叠视图内的可视区域上才能被计算。再重复一下,这就是为什么如果将摄像机尽量靠近前向平行以获得更好结果的一个原因。
对于处理非畸变的校正立体图像,块匹配立体匹配算法有以下三个步骤。
1)预过滤,使图像亮度归一化并加强图像纹理。
2)沿着水平线用SAD窗口进行匹配搜索。
3)再过滤,去除坏的匹配点。
十 从三维重投影获得深度映射
OpenCV中有两个函数帮助我们完成这项工作。第一个函数是:cvPerspectiveTransform();
第二个函数(也是新函数)cvReprojectImageTo3D()是操作整幅图像。
个人公众号: