群体智能算法之模拟退火算法

1. 简介

模拟退火算法是一种通用的概率算法，用于在一个大的搜寻空间内寻找问题的最优解。这种思想来源于物理中固体退火的过程，即将固体加热到足够的温度的时候，再缓慢冷却。温度升高时候，固体内部粒子随着温度升高变为无序状态，内能增大，而缓慢冷却的时候粒子却又逐渐趋近于有序状态。实际上这一思想是在一个过程中寻求系统能量最小的一种算法方式，在任意温度下，系统的能量都可以达到热平衡状态，而冷却到最低温度的时候是系统能量最低的状态。在任意一个温度下都可以达到热平衡状态，这是一个重要的步骤，可以由Monte Carlo模拟，但是这需要大量采样处理，工作量非常大。Metropolis提出这样的一种采样的方法，即设从当前的状态$i$生成新的状态$j$，如果新状态的内能小于状态$i$，($E_j<E_i$)那么 接受新状态$j$作为新的当前状态；否则，以概率$exp(-\frac{E_j-E_i}{kT})$接受状态$j$，其中$k$为Boltzmann常数，这一准则被称为Metropolis准则。

2. 算法基本原理

物理退火算法由以下三个过程组成：

1. 加热过程，用于增强粒子的运动，使其偏离平衡位置，温度足够高的时候，系统原先的均匀平衡状态变为非均匀状态。
2. 等温过程。对于与周围环境交换热量而温度不变的封闭系统，系统状态的自发变化总是朝着自由能减少的方向进行，当自由能达到最小的时候，系统达到平衡状态。这一过程对应于Metropolis抽样过程。
3. 冷却过程。使得粒子热运动减弱，系统能量逐渐下降，得到能量最低的稳定状态。

算法中需要控制的参数有：

• 控制参数的初始温度$T_0$，即冷却开始的初始温度。
• 控制参数温度$T$的衰减函数：将连续降温中的温度点离散化成降温过程中一系列温度点。
• 控制参数$T$的终止值$T_f$，即停止原则。
• Markov链的长度$L_k$，即任意温度条件下的迭代次数。

2.1 算法的基本步骤

① 令$T=T_0$，即开始退火的最初始温度，随机生成一个初始解$x_0$，并且计算相应的目标函数值$E(x_0)$。
② 令$T$等于下一个冷却进度表中的值$T_i$。
③ 根据当前解$x_i$进行扰动，并产生一个新的解$x_j$，计算相应的目标函数值$E(x_j)$，得到$\Delta E=E(x_j)-E(x_i)$。
④ 若$\Delta E<0$，那么新的解$x_j$被接受并作为当前状态的新的解；若$\Delta >0$，那么新的解$x_j$按照概率$exp(-\frac{\Delta E}{T_i})$接受，$T_i$为当前温度。
⑤ 判断$T$是否已经达到$T_f$。若是则停止算法，否则继续执行步骤②。

2.2 参数的选择原则

控制参数$T$的初始值$T_0$：一般意义上来说，对于退火算法都采用大范围下的粗略搜索与局部的精细搜索相结合来搜索全局最小值，所以足够大的$T_0$才能满足算法的条件，但是对于不同问题有不同的取值。
控制温度$T$的衰减函数：一般有多种控制温度$T$的衰减函数，常用的衰减函数可以表示为
$$T_{k+1}=\alpha T_k,k=0,1,2,...$$

其中$\alpha$是衰减常数，一般取值为$\alpha =0.5\sim 0.99$之间，这个常数决定了降温的过程。
Markov链选取的长度：Markov链选取的原则是：在控制参数$T$的衰减函数已经选定的情况下，$L_k$应当能够使得在控制参数$T$的每一取值上达到平衡状态。

3. 简单的例子

退火算法应用的场景有很多，我们现在对TSP问题、聚类问题以及在神经网络中的一些应用来进行探讨和分析。

TSP问题

TSP是最为典型的NP完全问题，即最坏情况下的时间复杂度随着问题规模的增大按照指数方式增长，目前来说并没有找到一种多项式时间内最有效的算法。
TSP问题可以描述为：已知$n$个城市坐标信息，某一个旅行商从某个城市出发访问每个城市一次并且仅访问一次，最后回到出发的城市，如何安排使得其行走的路线最短。TSP问题的解空间是所有遍历$n$个城市的路径，设城市的集合为$X=\{1,2,..,n\}$，$X$中的元素表示对$n$个城市的编号，其问题是寻求一个$n$个城市的排列$\pi (X)=\{V_1,V_2,...,V_n\}$，使得代价函数：
$$S_d=\sum _{i=1}^{n-1}d(V_i,V_{i+1})+d(V_n,V_1)$$

取得最小值，其中$d(V_i,V_{i+1})$表示城市之间的距离。

TSP问题中，新的解产生主要是通过以下两种方式来产生：
① 二变换方法：任意选取序号$u,v,(u<v<n)$，交换$u$和$v$之间的访问顺序。
② 三变换方法：任意选取序号$u,v,w,(u\le v<w)$，将$u$和$v$之间的路径插入到$w$之后访问。

目标函数差值：新求解的解与当前解的差值 $\Delta S=S_d-S{{}^{\prime }}_d$
Metropolis准则：以新的解与当前解的目标函数差定义接受概率，即
$$p=\{\begin{array}{ll}1& ,\Delta S\\ exp(-\frac{\Delta S}{T})& ,\Delta S>0\end{array}$$
我们选取这里的TSP问题数据集：TSP问题数据集。在本文中我们选取kroA200.tsp进行求解。
经过退火算法的计算之后，最优路径如下图所示：

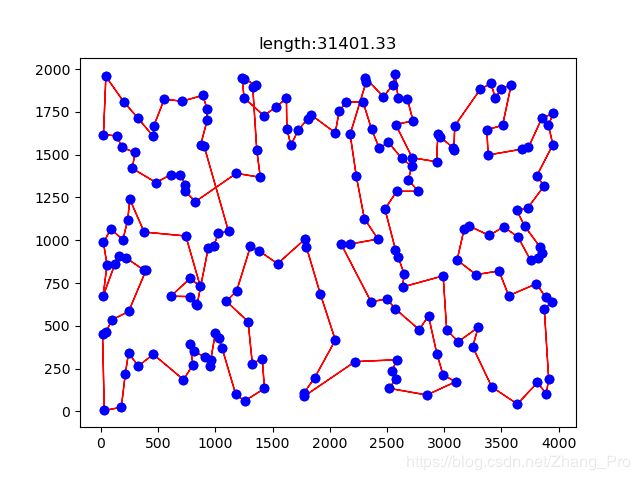
退火算法中最短路径长度的求解在每一次迭代中的长度变化如下所示：

具体代码参见笔者github，退火模型有python版本和MATLAB版本。

4.小结

模拟退火算法是一类以统计力学为基础的概率算法，通过求解系统能量最小的办法来在每一个Markov链中搜寻最优值。模拟退火算法具有较强的全局搜索能力，但是非常需要一些问题的经验和算法的实践过程。模拟退火算法非常适用于解决组合优化的问题，即目标针对有很多可能解的有限离散系统，最小化它的代价函数。上述算法中的能量分布解释称为数值意义上的代价函数，温度$T$成为了控制参数。
模拟退火算法与传统的迭代算法是有些不同点的：

1. 它不会陷入局部最小值，因为当系统在非零温度上运行时脱离局部最小总是可能的。
2. 模拟退火算法是自适应的，在高温过程中能够看见系统的大致轮廓，而它的具体细节在低温度的时候可以看出来。

参考文献

[1] MATLAB在数学建模中的应用，卓金武
[2] MATLAB智能算法30个案例分析（第2版）
[3] 神经网络与机器学习，Simon Haykin