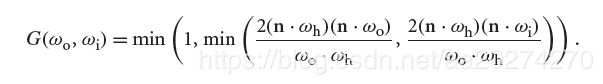PBRT_V2 总结记录 Microfacet 和 MicrofacetDistribution

概述

（这里 模拟一个金属表面，这个面是由 很多 很细的十分平滑的microfacets(微小的面)组成，这些microfacets 有自己的法线，对于整一个 表面的BRDF来说，需要传入 wi 和wo, 那么，只有那些法线是 wh 的 microfacets ，才会 从wi 方向 反射 光到 wo 方向上）

One of the first microfacet models for computer graphics was developed by Torrance
and Sparrow (1967) to model metallic(金属) surfaces. They modeled surfaces as collections of
perfectly smooth mirrored microfacets. The surface is statistically described by a distribution
function D(ωh) that gives the probability that a microfacet has orientation ωh
(recall Figure 8.12, which shows how roughness and the microfacet normal distribution
function are related).

 

Figure 8.12: Microfacet surface models are often described by a function that gives the distribution
of microfacet normals nf with respect to the surface normal n. (a) The greater the variation of
microfacet normals, the rougher the surface is. (b) Smooth surfaces have relatively little variation
of microfacet normals.

 

Because the microfacets are perfectly specular, only those with a normal equal to the halfangle
vector,

cause perfect specular reflection from ωi to ωo (Figure 8.15).

Figure 8.15: For perfectly specular microfacets and a given pair of directions ωi and ωo, only those
microfacets with normal ωh = ωi + ωo will reflect any light from ωi to ωo.

 

这个BRDF 的 公式：

其中：

D(wh)：distribution function D(ωh) that gives the probability that a microfacet has orientation ωh （判断一个 microfacets  的法线等于 wh 的 概率）

G(wo，wi) : geometric attenuation term, which describes the fraction of microfacets that are masked or shadowed, given directions ωi and ωo （衰减项）

 

One of the nice things about the Torrance–Sparrow model is that the derivation doesn’t
depend on the particular microfacet distribution being used. Furthermore, it doesn’t
depend on a particular Fresnel function, so it can be used for both conductors and
dielectrics.However, reflection functions other than perfect specular reflection cannot be
easily substituted: the relationship between dωh and dωo used in the derivation depends
on the specular reflection assumption.

（这个模型 不依赖 distribution function D, Fresnel function Fr，但是，这个Fr 最好是 镜面反射的，因为公式推倒的假设就是镜面反射）

 

Microfacet 类

class Microfacet : public BxDF {
public:
    // Microfacet Public Methods
    Microfacet(const Spectrum &reflectance, Fresnel *f,
        MicrofacetDistribution *d);
    Spectrum f(const Vector &wo, const Vector &wi) const;
    float G(const Vector &wo, const Vector &wi, const Vector &wh) const {
        float NdotWh = AbsCosTheta(wh);
        float NdotWo = AbsCosTheta(wo);
        float NdotWi = AbsCosTheta(wi);
        float WOdotWh = AbsDot(wo, wh);
        return min(1.f, min((2.f * NdotWh * NdotWo / WOdotWh),
                            (2.f * NdotWh * NdotWi / WOdotWh)));
    }
    Spectrum Sample_f(const Vector &wo, Vector *wi,
                              float u1, float u2, float *pdf) const;
    float Pdf(const Vector &wo, const Vector &wi) const;
private:
    // Microfacet Private Data
    Spectrum R;
    MicrofacetDistribution *distribution;
    Fresnel *fresnel;
};

1. 构造函数：

（因为 Microfacet  的 D 项是可以任意的，所以 D项 就抽象为 MicrofacetDistribution 类 ）

We now use the Torrance–Sparrow model to implement a general microfacet-based
BRDF. It takes a pointer to an abstract MicrofacetDistribution class, which provides
a single method to compute the D term of the Torrance–Sparrow model. This function,
MicrofacetDistribution::D(), gives the probability density for microfacets to be
oriented with normal ωh.

class MicrofacetDistribution {
public:
    // MicrofacetDistribution Interface
    virtual ~MicrofacetDistribution() { }
    virtual float D(const Vector &wh) const = 0;
    virtual void Sample_f(const Vector &wo, Vector *wi,
                          float u1, float u2, float *pdf) const = 0;
    virtual float Pdf(const Vector &wo, const Vector &wi) const = 0;
};

The Microfacet BRDF, then, just takes a reflectance, the Fresnel function, and a pointer
to a distribution.

 

2. Spectrum f(const Vector &wo, const Vector &wi) const;

Spectrum Microfacet::f(const Vector &wo, const Vector &wi) const {
    float cosThetaO = AbsCosTheta(wo);
    float cosThetaI = AbsCosTheta(wi);
    if (cosThetaI == 0.f || cosThetaO == 0.f) return Spectrum(0.f);
    Vector wh = wi + wo;
    if (wh.x == 0. && wh.y == 0. && wh.z == 0.) return Spectrum(0.f);
    wh = Normalize(wh);
    float cosThetaH = Dot(wi, wh);
    Spectrum F = fresnel->Evaluate(cosThetaH);
    return R * distribution->D(wh) * G(wo, wi, wh) * F /
               (4.f * cosThetaI * cosThetaO);
}

作用：

（代码就是公式的翻译，F.Evaluate 需要cosi, 所以就需要 cosh）

Evaluating the terms of the Torrance–Sparrow BRDF is straightforward. For the Fresnel
term, recall that the angle θh is the same between ωh and both ωi and ωo, so it doesn’t
matter which vector we use to compute the cosine of θh.We arbitrarily choose ωi.

 

3. 

 float G(const Vector &wo, const Vector &wi, const Vector &wh) const {
        float NdotWh = AbsCosTheta(wh);
        float NdotWo = AbsCosTheta(wo);
        float NdotWi = AbsCosTheta(wi);
        float WOdotWh = AbsDot(wo, wh);
        return min(1.f, min((2.f * NdotWh * NdotWo / WOdotWh),
                            (2.f * NdotWh * NdotWi / WOdotWh)));
    }

作用：

（G 项，进行衰减）

The geometric attenuation termis derived by assuming that the microfacets are arranged
along infinitely long V-shaped grooves. This assumption is more restrictive than the
general term D(ωh) used to model the microfacet distribution and does not account
for the roughness of the surface, but yields a closed-form result, which is helpful for
efficiency. It is also easy to evaluate and matches many real-world surfaces well. The
attenuation term (omitting the derivation) is