一、 Traverse a tree
- Binary Tree Preorder Traversal
思路:
递归法很简单,不赘述。迭代法:先序遍历可分解为两段,沿最左侧通路自顶向下访问的各节点,以及自底向上遍历的对应右子树。
代码:
private void visitAlongLeftBranch(TreeNode node, Stack st, List res) {
while (node != null) {
res.add(node.val);
st.push(node.right);
node = node.left;
}
}
public List preorderTraversal(TreeNode root) {
List res = new ArrayList<>();
Stack st = new Stack<>();
TreeNode x = root;
while (true) {
visitAlongLeftBranch(x, st, res);
if (st.empty()) break;
x = st.pop();
}
return res;
}
- Binary Tree Inorder Traversal
思路:
递归法很简单,不赘述。迭代法:沿最左侧通路自底向上,以沿途各节点为界,遍历其右子树。
代码:
private void goAlongLeftBranch(TreeNode node, Stack st) {
while (node != null) {
st.push(node);
node = node.left;
}
}
public List inorderTraversal(TreeNode root) {
List res = new ArrayList<>();
Stack st = new Stack<>();
TreeNode x = root;
while (true) {
goAlongLeftBranch(x, st);
if (st.empty()) break;
x = st.pop();
res.add(x.val);
x = x.right;
}
return res;
}
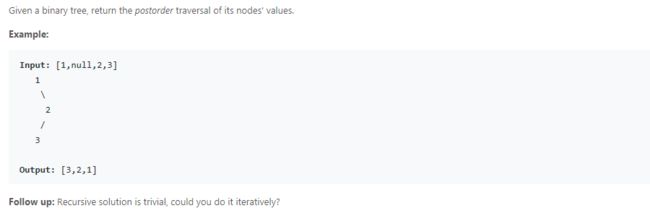
- Binary Tree Postorder Traversal
思路:
递归法解决,迭代法过于麻烦,按下不表。
代码:
public List postorderTraversal(TreeNode root) {
List res = new ArrayList<>();
inorder(res, root);
return res;
}
private void inorder(List res, TreeNode node) {
if (node == null) {
return;
}
inorder(res, node.left);
inorder(res, node.right);
res.add(node.val);
}
二、Solve Tree Problems Recursively
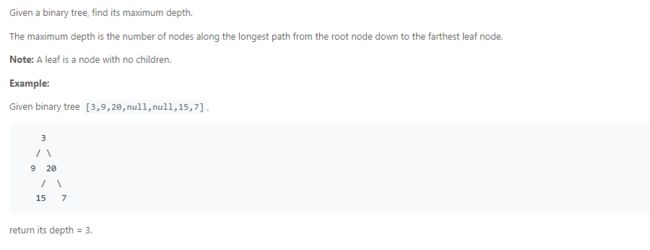
- Maximum Depth of Binary Tree
思路:
比较简单,不赘述。
代码:
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int left_depth = maxDepth(root.left);
int right_depth = maxDepth(root.right);
return Math.max(left_depth, right_depth) + 1;
}
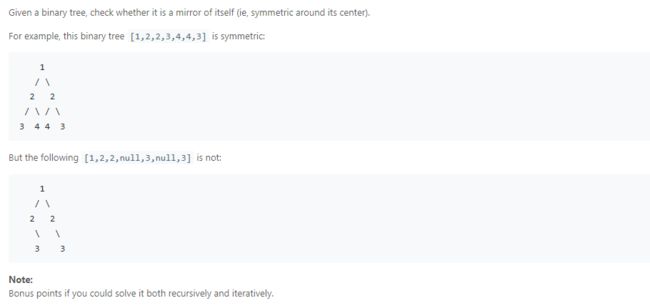
- Symmetric Tree
思路:
比较简单,不赘述。
代码:
public boolean isSymmetric(TreeNode root) {
return root == null || isSymmetricHelp(root.left, root.right);
}
private boolean isSymmetricHelp(TreeNode left, TreeNode right) {
if (left == null || right == null)
return left == right;
if (left.val != right.val)
return false;
return isSymmetricHelp(left.left, right.right) && isSymmetricHelp(left.right, right.left);
}
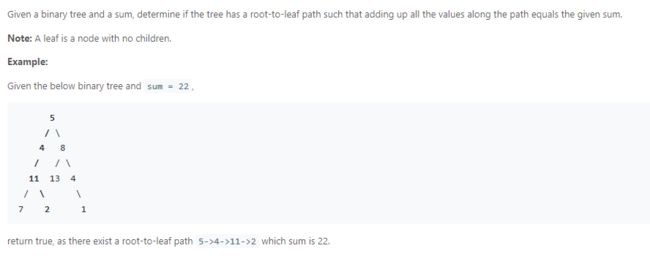
- Path Sum
思路:
比较简单,不赘述。
代码:
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) return false;
return preorder(root, 0, sum);
}
private boolean preorder(TreeNode node, int sum, int target) {
if (node == null) return false;
if (node.left == null && node.right == null && (sum + node.val) == target) {
return true;
}
return preorder(node.left, sum + node.val, target) || preorder(node.right, sum + node.val, target);
}
三、Conclusions
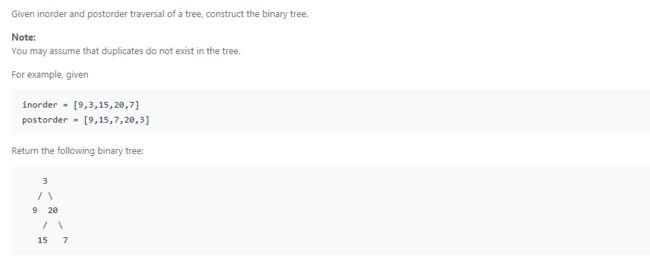
- Construct Binary Tree from Inorder and Postorder Traversal
思路:
代码:
public TreeNode buildTree(int[] inorder, int[] postorder) {
TreeNode root = build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
return root;
}
private TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {
if(inStart > inEnd || postStart > postEnd) return null;
TreeNode node = new TreeNode(postorder[postEnd]);
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == postorder[postEnd]) {
node.left = build(inorder, inStart, i - 1, postorder, postStart, postStart + (i - inStart) - 1);
node.right = build(inorder, i + 1, inEnd, postorder, postStart + (i - inStart), postEnd - 1);
}
}
return node;
}
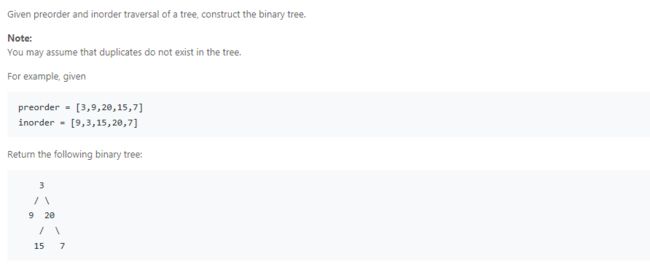
- Construct Binary Tree from Preorder and Inorder Traversal
思路:
代码:
public TreeNode buildTree(int[] preorder, int[] inorder) {
TreeNode root = build(inorder, 0, inorder.length - 1, preorder, 0, preorder.length - 1);
return root;
}
private TreeNode build(int[] inorder, int inStart, int inEnd, int[] preorder, int preStart, int preEnd) {
if(inStart > inEnd || preStart > preEnd) return null;
TreeNode node = new TreeNode(preorder[preStart]);
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == preorder[preStart]) {
node.left = build(inorder, inStart, i - 1, preorder, preStart + 1, preStart + (i - inStart));
node.right = build(inorder, i + 1, inEnd, preorder, preStart + (i - inStart) + 1, preEnd);
}
}
return node;
}
- Populating Next Right Pointers in Each Node
思路:
可以在层序遍历的基础上改进,也可以递归解决,详情见代码。
代码:
层序遍历改进:
public void connect(TreeLinkNode root) {
Queue queue = new LinkedList<>();
List> wrapList = new LinkedList<>();
if (root == null) return;
queue.offer(root);
while (!queue.isEmpty()) {
int levelNum = queue.size();
List subList = new LinkedList<>();
for (int i = 0; i < levelNum; i++) {
if (queue.peek().left != null) queue.offer(queue.peek().left);
if (queue.peek().right != null) queue.offer(queue.peek().right);
subList.add(queue.poll());
}
wrapList.add(subList);
}
for (int i = 0; i < wrapList.size(); i++) {
for (int j = 0; j < wrapList.get(i).size() - 1; j++) {
wrapList.get(i).get(j).next = wrapList.get(i).get(j + 1);
}
if (wrapList.get(i).size() == 1) {
wrapList.get(i).get(0).next = null;
}
}
}
递归:
public void connect(TreeLinkNode root) {
connect(root, null);
}
private static void connect(TreeLinkNode root, TreeLinkNode sibling) {
if (root == null) return;
else root.next = sibling;
connect(root.left, root.right);
if (sibling != null) connect(root.right, sibling.left);
else connect(root.right, null);
}
- Lowest Common Ancestor of a Binary Tree
思路:
当前节点如果是p,q的公共最先节点,则p,q一定在当前节点的左右子树中。可以用递归解决。
代码:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode ltree = lowestCommonAncestor(root.left, p, q);
TreeNode rtree = lowestCommonAncestor(root.right, p, q);
if (ltree != null && rtree != null) return root;
return ltree != null ? ltree : rtree;
}
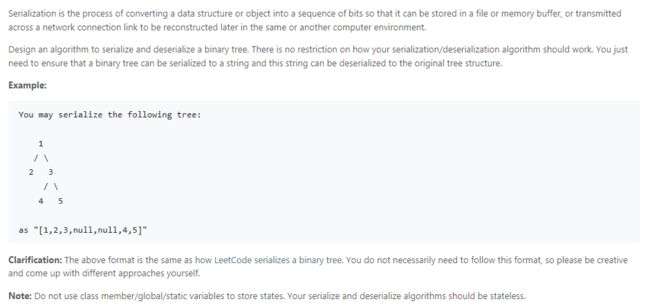
- Serialize and Deserialize Binary Tree
思路:
注意是如果是preorder的serialize,那就要对应的deserialize,不难。
代码:
// Encodes a tree to a single string.
public String serialize(TreeNode root)
{
if(root == null) return "#";
return "" + root.val + " " + serialize(root.left) + " " + serialize(root.right);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data)
{
return build(new Scanner(data));
}
private TreeNode build(Scanner sc)
{
if(!sc.hasNext()) return null;
String tk = sc.next();
if(tk.equals("#")) return null;
TreeNode root = new TreeNode(Integer.parseInt(tk));
root.left = build(sc);
root.right = build(sc);
return root;
}