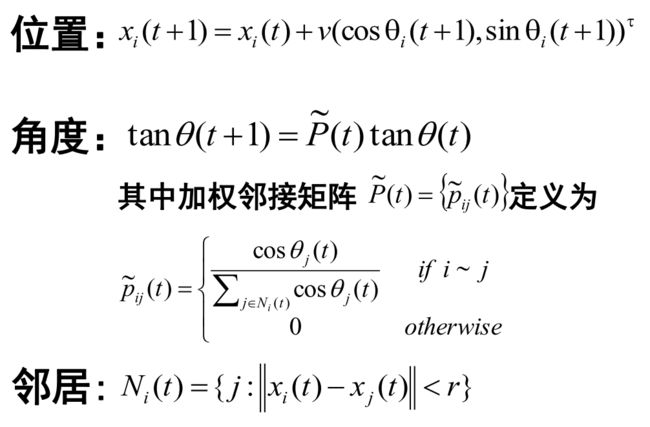预测考题
- Agent的定义/特点
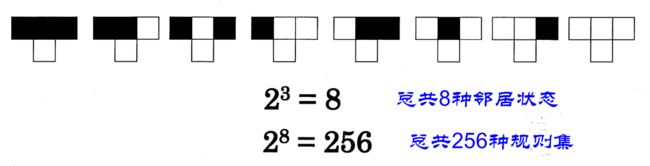
- 元胞自动机的特点
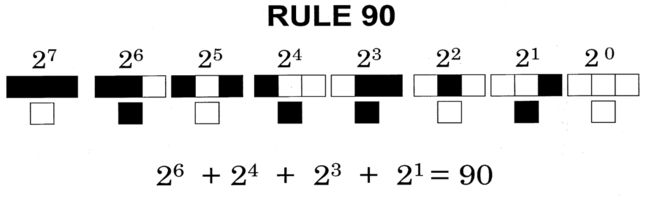
- 一维自动机规则编码
- GA的伪代码
- Wolfram 的分类
- MAS的控制方法以及举例
- MAS和平均场的区别
1 Agent的特点、MAS的概念、特征
agent是一个计算单元,是自动的,能够与其他的agent互动,从环境中获取信息,由目标或者行为策略驱动。
MAS是由大量局部相互作用的个体组成,不借助中央控制,能够涌现出宏观现象的系统
2 平均场 VS MAS
模型和模拟的区别
- 模型是对某种现象/某个系统的数学刻画
- 模拟是模型的某种实现,例如计算机实现
即使模型完全确定,模拟结果也不一定可预测分析(即使是非常简单的模型:the three bidies)
掌握2种对复杂系统的建模方式(平均场和Agent-based) 捕食-被捕食的Lotka-Volterra方程和MAS建模方法、传染病模型
- 微分方程建模:平均场方法(粗)
- 用统一的长程作用代替局部相互作用
-
所得到的解,是随时间演化的空间上的平均
- MAS建模:基于Agent的建模(细)
-
局部相互作用不能被平均掉,必须考虑局部相互作用在不同 空间位置所带来的不同的效果
-
传染病模型
S (for susceptible,易感), I (for infectious,感染), R (for recovered, 免疫)
- SIS
无法免疫,但能痊愈,反复得病 - SIR
一次得病,终身免疫 - SI
无法恢复 - SIRS
能恢复,有限免疫
平均场建模
3 元胞自动机
最简单的MAS模型
特点:
离散状态、位置、时间
确定的、相同的更新机制
-
同步更新
John von Neumann的机器自繁衍 (1940s)
John Conway 的生命游戏 (1970s)
0->1:周围恰好3个
1->0:周围不是2或3-
Stephen Wolfram 的分类(1980s)
- 静止(不动点) homogeneous state
- 周期性为(极限环) a set of separated simple stable or periodic structures
- 混沌(初始条件敏感性)* chaotic pattern
- 带结构的有序(复杂性)complex localized structures, sometimes long-lived.
实际运用举例:
- 用于教室突然安静
8,9 集体行为
在整体涌现出个体单独存在时所不具备的行为特征。简单规律造就复杂现象;被分割的部分如何整合,强调各部分之间的关联
- 自发行为的分析 自下而上
给定agent的局部规则,系统整体涌现出什么行为? 自组织行为,统计物理,Vicsek模型的同步性分析 - 局部规则的设计 自上而下
给定期望的集体行为,如何设计agent的局部规则? 群体智能(蚂蚁算法),分布式控制设计 - 干预
给定agent的局部规则,如何干预系统的集体行为?- 软控制
- consistent moving shill
- leader-follower
往往有少数个体带目标信息(方向明确,固定角度的shill),这些个体可以帮助诱导整个群体
邻居半径越大– shill 影响范围更大,但shill 影响强度变弱. 对于集中的leader,方向固定的话,影响半径越大越好;方向可变的话,半径越小越好
优点:
不需要设计leader的运动规则
不需要每个时刻都测量群体的信息
缺点:
需要的leader数目较多
没有反馈,对噪声不具有鲁棒性
是在概率框架下同步,不是确定性框架
- 牵制控制 Pinning control
通过有选择地对网络中的少部分节点施加控制而使得整个网络达到所期望的行为。
举例:广告商花钱请大V转发宣传
- 软控制
10 Vicsek模型的同步分析
同步是一种微观的趋同行为的涌现
Vicsek模型
其中,角度是直接由相邻角度确定的,不是增量形式改变;自身的角度当作相邻个体的角度之一。位置的变化是增量形式的。
定理1:在G不变且连通的情况下,任意的初始角度都会演化到同步角度
定理2:G在每一时刻都保持连通的情况下,任意初始角度都会演化到同步角度
定理3:存在时间的一个划分,G在每个时间区间上都联合连通,则对任意角度都会演化到同步角度。其中,联合连通是指G的并
确定性框架下的同步研究的是依赖于初始条件和系统参数的同步条件
随机框架下是指所有个体的位置和角度的随机化假设
相互作用的图表示:无向图,结点带环。图由系统个体位置决定,反过来,图也决定系统的动力学演化,
11 静态局部规则——离散优化
难易问题分类
染色问题(The Coloring Problem, NP-complete; Network problem; Combinatorial Optimization)
Effective ≠ Efficient
P : 易处理 tractable problems iff. it can be solved by a Polynomial time algorithm.
NP : intractable problems iff. it can be solved in Polynomial time by an Nondeterministic algorithm (Nondeterministic Turing Machine). 非确定图灵机可以对分支情况同时处理
算法实现
特殊结构问题
- 贪心算法
每步都是找一个当前局部最优点, 不考虑未来. - 动态规划 (DP)
对前面的决策所形成的状态而言,余下的诸决 策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
通用搜索问题
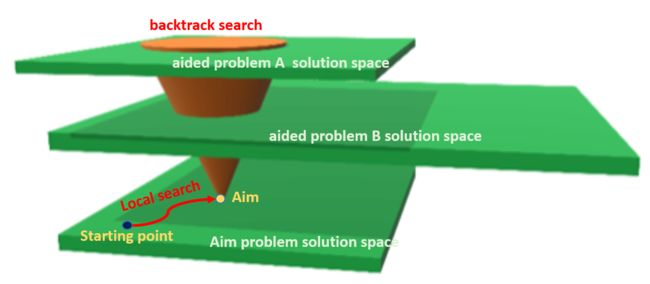
- 回溯 Backtracking
assign values to variables sequentially .e.g. 前缀搜索prefix searching
too slow (but complete)
将解空间进行树状划分,从局部确定到完整确定。 -
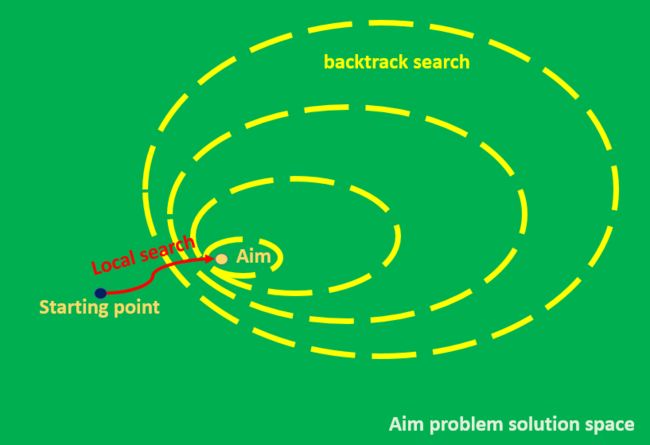
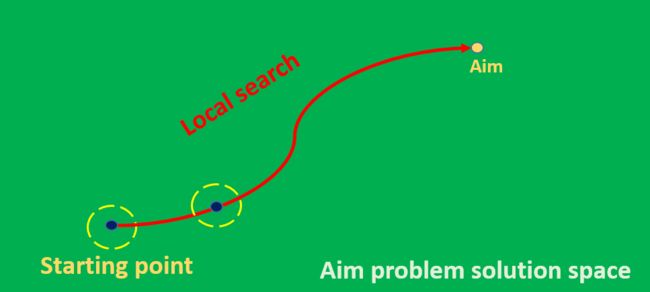
启发式搜索 Heuristic Search
local search. a possible configuration of all variables, test. Most practical and powerful one, but Incomplete and it is based on intuition and experience.
从解空间的一个点出发,根据局部信息,到达认为的一个最解。可以看作是一个解的演化过程,也是MAS关注的求解形式。可以同时处理多少个解: GA遗传算法, 粒子群优化…
我们怎样在解空间进行导航?
借助评估函数 Evaluation Function
没有一个算法可以在所有的问题实例中战胜其它所有的算法(no free lunch 理论)
Local search 在MAS系统问题求解中的体现
local search 优点: 1. 并行运算Parallel Computing 2. 实际更可行 More feasible in some cases
MAS系统的最优解就是纳什均衡点Nush Equilibrium: NE is a system state that no single agent can benefit from unilaterally changing his action
Zero sum games (two-person): Maximin strategy (MS) is a solution 对于零和博弈,极大极小是一个解
(xi, xj)=1当两个顶点相连时等于1否则等于0. 自身认为是相连的。
LEF & GEF in coloring problem
把每个结点看作一个agent,agent的状态就是颜色,系统演化就是每个agent接收周围agent的状态,根据自己的策略,确定自己的状态,直到系统演化到解。
模拟退火sumulated annealing, GA, 粒子群优化particle swarm optimization 使用的是GEF.
LEF仅使用局部信息,每次仅改变局部状态
Consistency between LEF and GEF
Nash Equilibrium and local optimum 如果连接权重是对称的话,则两者等价
Symmetrical interaction: if gij(xi , xj) = gji(xj , xi) The LEF is consistent with GEF=∑LEF
12 静态局部规则——复杂网络
网络是刻画MAS系统的一种方式
13 网络模型概念
-
平均距离L
是所有的顶点之间距离的平均值
-
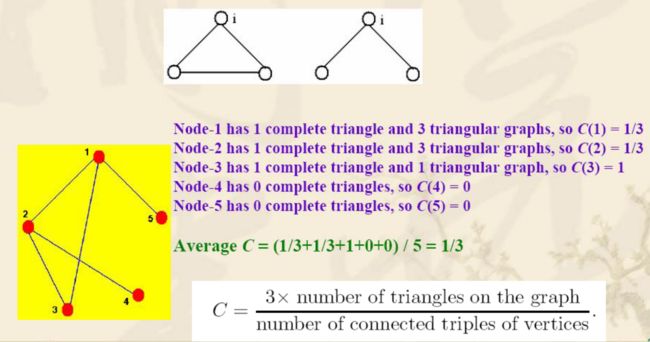
聚类系数C
-
度分布
分母为总结点数/分子为对应度结点的个数
环形网络
其中K是每个顶点的度数。所有的顶点度数相等
-
平均度
-
团组
connections are sparse but within which connections are relatively dense.
结点的层级
第一级:反复将1度顶点去掉,这些结点构成第一级
第二级:反复将2度顶点去掉,这些结点构成第二级
...
-
motif
各种模式的子图,构成复杂网络的block
不同类型的实际网络,各种motif的分布不同,相当于网络的特征
-
介数
在各种社会网络中,如(朋友网,合作网,微博等 ),哪些是最活跃、最具影响力的人?在艾滋病传播中,哪些是最危险的人? 在通信网络或者交通网络中,那些节点承受的流量 最大?不是只考虑度的大小。
-
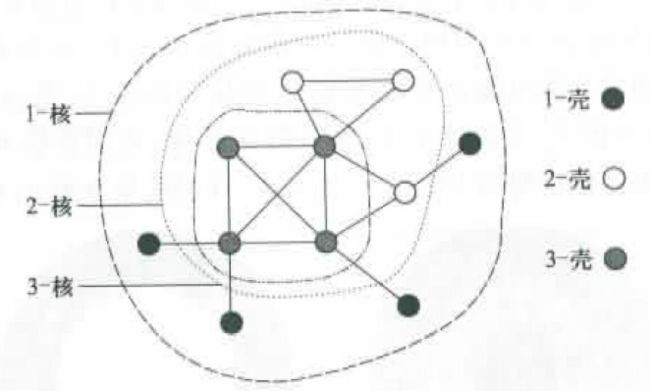
核数
在一个网络中,我们重复去掉所有度为k的节点,剩下的子网络称为k-核,被去掉的的节点及它们之间的边称为k-壳。
平均核数大 -> 对随机失效和有意攻击都具有 鲁棒性
14 复杂网络模型
-
随机图ER
每两个顶点之间连接的概率为P.
显然平均度数
-
small-world
从规则图开始:给定一个含有N个点的环状最近邻耦合网络, 每个节点都与它左右相邻的各K/2个节点相连,K为偶数
随机化重连:以概率p随机地重新连接网络中原有的每条边(i,j), 即把每条边的端点i保持不变,端点j改取为网络中随机选择的一个节点,其中规定不得有重边和自环。和社交网络很相似:小团体中存在与其他团体连接的人从生成过程来看,SW模型在p很小的时候,具有规则图的特性; 当p慢慢增大时,逐步向随机图的性质转变
因为只是随机重连,因此平均度不变,为
例子:
食物链网络、代谢网络、学术合作网络
-
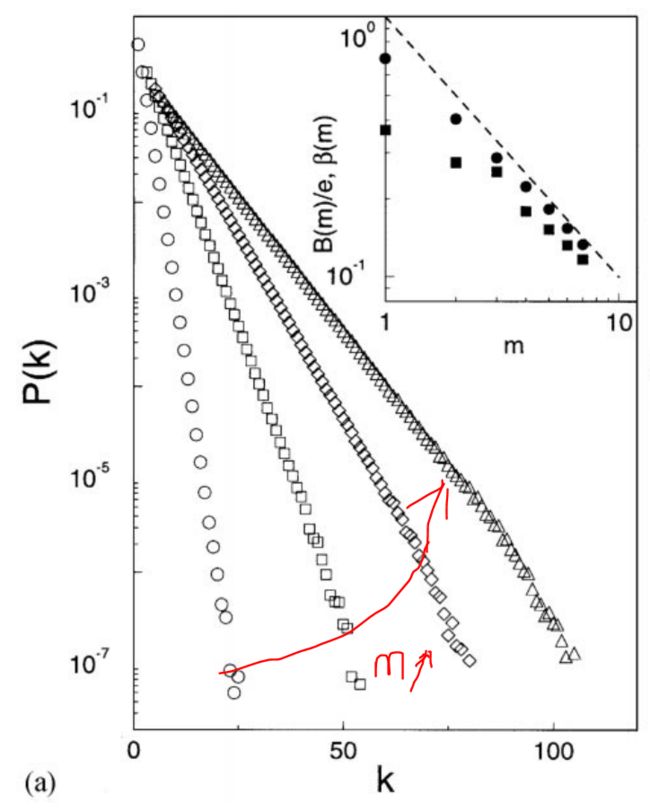
scale-free网络
scale-free/ Power-Law distribution. 注意:幂律分布不是指数分布!
所有的scale-free网络都具有小世界特性,但不是所有具有小世界特性的网络都有 scale-free特性
前面两个网络都是固定的顶点数N,而实际的网络都是顶点数不断生长的(具备生长特性的实际网络往往满足scale-free)。(不过增长的网络的关系一般不满足对称性)另外一点是,顶点之间连接不是等可能的,而是有偏好的。
网络需要结合生长性和偏好性连接才能得到scale-free网络: the combination of growth and preferential attachment is utimately reponsible for the scale-free distribution and power-law scaling observed in real networks. 一开始有m_0个顶点,没有边,每一时刻增加一个顶点,并从这个顶点出发连接m条边,
幂律的系数与m^2成比例
例子:
- 论文引用网络
- WWW万维网
网络算法 PageRank
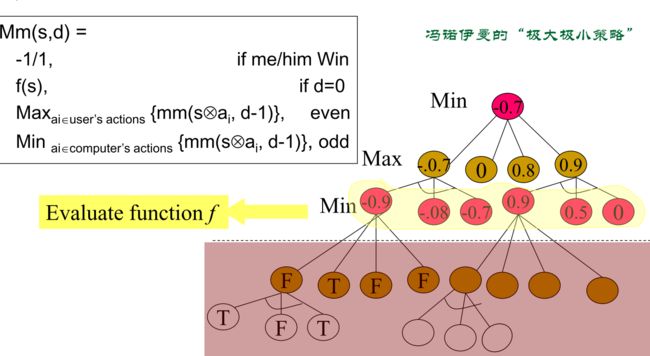
假设有一个网上的随机冲浪者,他从一个随机选择的页面开始浏览。如果当 前页面的出度大于零,那么以概率s(0 石头剪刀布属于:两人博弈、非合作博弈、零和博弈、静态博弈、完全信息博弈 占优策略、剔除劣策略 与或输搜索:对于当前的局面,我可以有N种选择,只要有一个能够通往胜局,则此时的局面也是胜局,因此是对我的行为导致的局面的OR运算;而对方面临棋局时,只要有一个行动能产生我的败局,则当前局面也是我的败局,因此是对对方所有可能行为导致局面的AND运算。所以我的策略是对当前局面进行一个OR-AND Tree进行搜索: 上述方法需要依靠最终的胜局和败局来递推当前局面。这个树太大了,所以无法得到底布情况,于是在不到底部就需要对那时的局面进行评估:1表示胜局,0表示败局的话,中间值就是对一个局面的评价值,越大表示对我越有利。OR/AND运算就转变成呢MAX/MIN运算 启发于:Fisher的群体遗传学 多人可重复的囚徒困境博弈The Evolution of Strategies in the Iterated Prisoner’s Dilemma 如果记忆长度是1,则编码序列有4位: CC|CD|DC|DD ,Tic-for-tak的编码为CDCD 它不能处理互动作用同时发生于多于两个个体的博弈 概念: 例子:15 复杂的相互作用——个体适应性:博弈
分类
静态博弈指在博弈中,参与人同时选择行动,或 虽非同时但后行动者并不知道前行动者采取了什么 具体行动;动态博弈指的是参与人的行动有先后顺序,且后 行动者能够观察到先行动者所选择的行动的博弈(下棋)
完全信息指的是每一个参与人都知道其他参与人的策略集合 及收益函数;否则就是不完全信息
求解(即双方非采取什么策略)
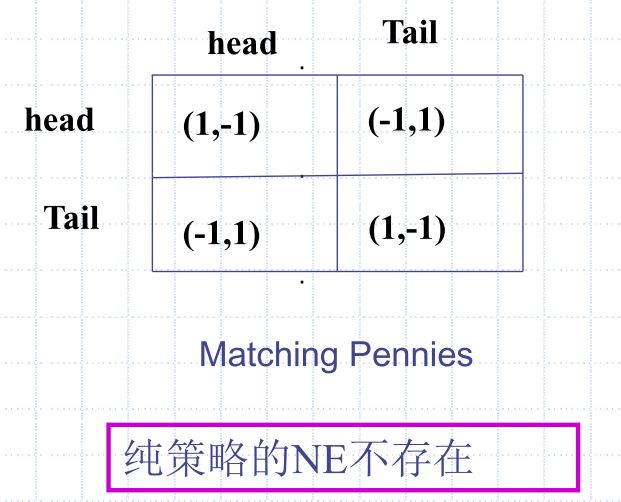
占优策略一定是NE,NE可能存在多个,可能不存在纯策略NE,但一定存在混合策略NE。NE不一定是全局最优解零和博弈:纳什均衡就是极大极小
评价函数的设计
16 复杂自适应系统——群体自适应:群体从进化论到遗传算法
多遗传单位决定性状
鲁棒性: 基因发生突变后,表现型不发生变化 (如果外界环境不发生变化,适应性就不发生变化。)
适应性:突变率不变的情况下,一个群体在环境改变后,是否很快演化出相对新环境最适应的表现型
例子:对于基础理论/全新理论研究的支持。在当下与传统方法相比效果没那么好,但是对于市场变换适应强(理论基础更强,共容易改进)17 群体自适应——遗传算法
如果基因之间是相互独立的,那么找到最佳组合的时间是线性增加的,而如果是两两相关的,那么需要指数增加的时间
building block是层级结构的基础GA
GA特点
18 复杂自适应——群体策略演化
一个策略就是一个决策规则,与历史相关. 策略甚至可以将对方的策略(一般是自己猜测)作为输入,针对性地做出决策。
好的策略特点:善良、宽容、报复、清晰GA进行策略演化
如果记忆长度是3,则编码序列有2^(2*3)=64位Evolutionarily stable strategy (ESS)
背叛策略-> (合作策略->针锋相对):All-D本身不能入侵TFT,但是All-C可以,而被All-C入侵后,All-D就可以入侵了。加入噪音
如果上一局是:对方占我便宜或双方背叛,那么这一轮我就换另一种策略;如果上一局是:我占了便宜或者双方合作, 这一局我就维持上一局的策略不变。比TFT更适应偶发失误(是因为双方背叛不会一直持续),也能防止AllC(噪音使得Pavlov占便宜)和AllD(AllD对Pavlov,得分是平均3分(5、1、5、1 ….) Pavlov对自己也是平均3分。 但是AllD跟自己打是平均1分。 所以不能入侵Pavlov)的入侵19 CAS(Complex Adaptive Systems) 复杂自适应系统
细胞、语言、生态环境