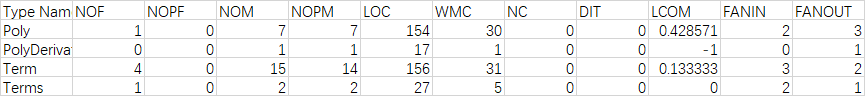前三次作业总结主要分为以下几个部分的内容:
- 数据抽象与类的设计
- 重构代码和功能的泛化
- 程序bug检验
- 基于度量的程序结构分析
数据抽象与类的设计
数据管理类
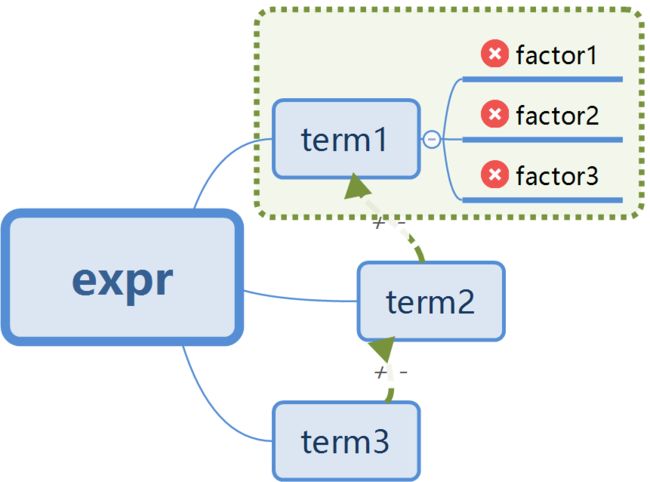
面向对象核心思想之一——“万物皆为对象”,在学习面向对象的编程伊始具有重要的意义。因为只有明确了程序依据数据抽象进行分类而不是依据算法执行的过程进行分类,才能在最开始设计程序时摆脱面向过程编程的烙印。第一次作业的内容是对多项式进行求导计算。本着数据抽象的原则,不妨来分析一下我们将要使用哪些数据(: 以及多项式的构成。
- 表达式→ 项{±项}
- 项 → 因子{*因子}
从文法中可以直接看出,数据分成了三个层次,表达式,项和因子,所以对于三个层次的数据需要分别建立一个类来进行管理。进一步分析这几个类之间的关系,不难发现,项是由因子通过乘法关系耦合而成,多项式是由项通过加减法的关系耦合而成。
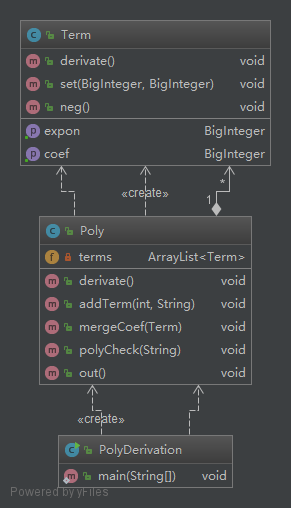
这样数据管理类就基本完成了,之后,需要为了方便,求导这一功能可以自顶而下的执行,如expr的求导需要调用每个term的求导规则,然后加起来,term的求导则需要调用底层的factor类的求导规则。这样把各个层次的求导规则按照逻辑关系屏蔽开,实现起来方便简洁。在以后的作业中看待问题的思路和角度,要从数据抽象管理、层次关系管理、复杂性屏蔽等多个角度来看待,这样才是真正使用面向对象的思路来解决问题。最终第一次作业的UML图如上所示。对于第二三次作业的分析,将会在重构代码的过程中进一步阐述清晰。
数据输入部分
数据输入的处理需要包括两个功能:1.能够识别出错误的输入格式,并且进行异常处理。2.能够分析数据形式,并且创建相应的数据类。
对于异常处理部分采用Java语法的try-catch机制,如果在读入的过程中遇到不符合输入格式要求的字符串,则抛出异常,并且由上层相应的函数处理该异常。这样的设计一方面作业要求的错误被看作不合法输入,另一方面,由于自己代码编写导致的异常如除以零超出数据范围等都会被视作不合法的输入。如下图中所示的关系,在编写代码的过程中,需要保证程序所实现的格式错误逼近规定的格式错误。这样的坏处是,程序运行时的错误可能被认作是格式错误,优点则是编写的程序在任何时候都能保证不出现crash的情况。更进一步的,如果在输入处理阶段的异常看作是输入格式错误,对在功能调用时出现的异常加以细化的处理和提示信息,上述不足就基本被弥补了。
本次作业输入处理经过和同学的交流发现,主要是分为两个派别:1.采用编译原里中的思想,递归下降处理输入的字符串。2采用正则表达式直接抓取相应的字符串并且进行匹配。在前三次实验中,助教推荐的方法前两次都是方法2,但是最后一次却推荐方法1。笔者认为如果在之前的作业中采用了递归下降子程序,第三次继续采用无可厚非。但是递归下降子程序本身相对复杂,把处理过程中的诸多情况都需要coder自己来控制,正如编译原理课程设计实验课一样,在代码中会有大量的if-else结构,既不美观,也容易产生bug。第三次作业如果转投方法1,无疑会大量增加可避免编码复杂度。所以笔者在三次作业一以贯之地都采用了正则表达式的方法,并且逐渐学习了更多正则表达式的技巧。
第一次作业
使用正则表达式的捕获组,进行处理。相信很多同学都会遇到group捕获顺序的问题,在第一次作业中,因为正则表达式相对简单,所以可以人工控制捕获组,如下图所示正则表达式,把他们由繁到简直接连接起来,然后匹配,查找每个捕获组是否为NULL,则可以知道是否匹配成功了某个正则表达式。可以抓取出一个factor字符串,并且对factor建立相应数据管理类的实例。
1 "([+-][+-]?\\d+\\*x\\^[+-]?\\d+)" 2 "([+-][+-]?x\\^[+-]?\\d+)" 3 "([+-][+-]?\\d+\\*x)" 4 "([+-][+-]?x)" 5 "([+-][+-]?\\d+)"
第二次作业
在第二次作业中,增加了sin(x)和cos(x)这两项,factor的组合情况变得更多了,所以正则表达式变得更加复杂。手动控制捕获组的难度加大,所以在第二次作业时引入了忽略组的技巧。(?: )表示捕获组中将忽略该括号中的表达式,所以对于想捕获的内容只需要用他自己并且group(0)中就可以找到,而不用担心有其他的捕获组来进行干扰。
1 String facA = "(?:[+-]?[+-]?\\d+)"; 2 String facB = "(?:[+-]?x(?:\\^[+-]?\\d+)?)"; 3 String facC = "(?:[+-]?S(?:\\^[+-]?\\d+)?)"; 4 String facD = "(?:[+-]?C(?:\\^[+-]?\\d+)?)";
第三次作业
第三次作业中增加了嵌套这一规则。嵌套规则的核心是递归处理——相同子问题的处理。所以对于第三次作业只需要想好最平凡的情况处理,以及嵌套()之外的处理方式,括号内的部分可以使用递归来解决。所以问题分解为两个部分(1)处理屏蔽最外层括号的情况(2)递归处理括号内的嵌套。为了解决这两个问题,必须在正则表达式中直接匹配屏蔽括号内的部分。如sin((x+2*sin(x)^3))+cos(x),我们希望能够直接得出sin(·),并且得到括号内的部分(x+2*sin(x)^3),进而递归处理。很多同学第一反应是使用正则表达式"\\(.+\\)"来进行匹配,但很遗憾的是,JAVA的正则表达式匹配无法支持括号嵌套功能,上述表达式在sin((x+2*sin(x)^3))+cos(x)中会匹配得到sin((x+2*sin(x)^3))+cos(x)而不是sin((x+2*sin(x)^3))。
分析一下这个问题,发现正则表达式不支持括号匹配,所以分不清括号的的对应关系导致出错,那么如果我们能够进行手动控制括号匹配,就意味着可以继续使用正则表达式!
即,区分开内层括号和外层括号就能够实现屏蔽内层嵌套内容,实现正则表达式的匹配。我们借鉴了计算机语言中转义的思想,将最外层的'(' , ')'替换为'#',然后就可以通过"#[^#]+#"完美的实现括号嵌套屏蔽以及括号内部内容的抓取。
1 String facD = "(?:[+-]?[+-]?\\d+)"; 2 String facC = "(?:[+-]?x(?:\\^[+-]?\\d+)?)"; 3 String facB = "(?:[+-]?S#[^#]+#(?:\\^[+-]?\\d+)?)"; 4 String facA = "(?:[+-]?C#[^#]+#(?:\\^[+-]?\\d+)?)"; 5 String facE = "(?:[+-]?#[^#]+#)";
重构代码和功能泛化
考虑到三次作业的复杂程度逐渐增大,如何合理的重构代码是一件非常有意义的事情,对重构进行总结,既有利于我们写代码时注意延展性,也有利于在完成多个新需求、增加新功能时高效而又简洁。正如《重构——改善既有代码设计》中给程序员的建议"如果你发现自己需要为程序添加一个新的特性,而现有的代码结构使你无法很方便地达成目的,那就先重构那个程序,使特性地添加比较容易进行,然后再添加特性"。所以在第一次和到第二次作业之间和第二次作业到第三次作业之间,我们都不同程度地对原有地代码进行了重构。
第一次作业→第二次作业
第二次作业与第一次作业相比,因子不在单纯地只有x(所以在第一次作业中没有实现term就可以囊括所有因子),而是增加了sin(x) 和cos(x)。
原本第一次作业中term的求导方式发生了变化。原来term可以作为最小部分求导,现在必须区分开x和sin(x),所以针对x求导规则重新写了一个新的方法dX(),依次来和未来的dCosx() dSinx()并列。
在第一次作业中同类项的合并项第一次作业写在了Poly类中,但是在第二次作业中发现Poly类过于臃肿,而且合并同类相是以term 为单位,故增加了中间层terms来管理所有的term,并且将mergeCoef(合并同类项)的功能在terms中实现。
写完第三次作业发现的不足
- 没有明确将sin(x) cos(x) x 这三个因子作为类重构出来。统一混在term中混淆了项和因子的概念。这样导致因子的求导法则混淆在项中,他们之间完全是并列的关系所以应该拆分。
- 没有区分好expr 和term的概念,输入部分完全混在Poly类中,虽然进行了一定的重构,但是Poly类依然过于臃肿,不方便增加新功能和维护阅读
第二次作业→第三次作业
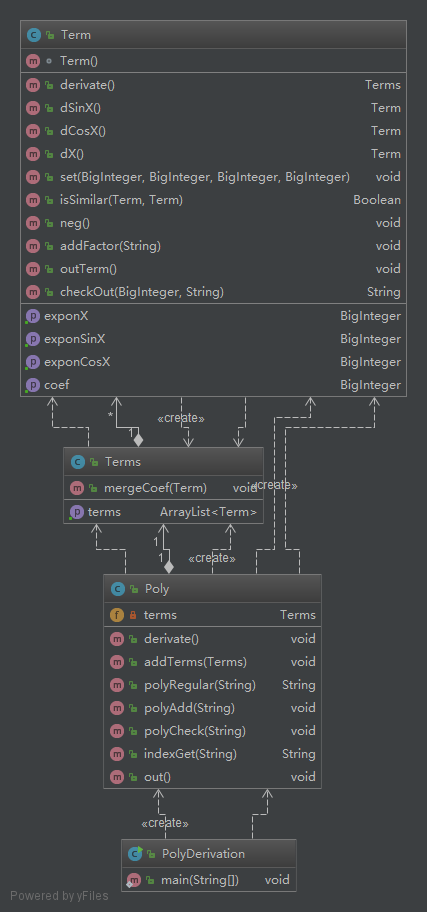
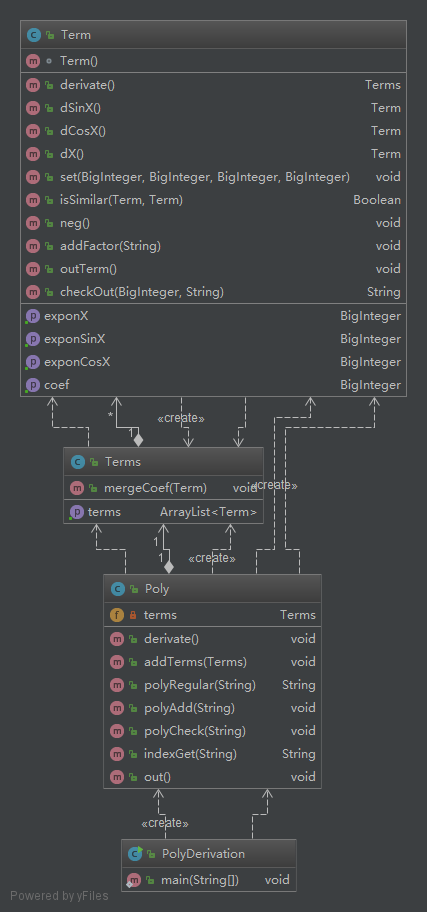
重构最开始就发先应该对现有的因子进行重构。并且之前受系数的影响没有提出常数项因子的概念,所以在第三次作业最开始重构的就是因子部分。
常数、sin(x)、cos(x)、x的父类factor规定了因子的特性,在常数中expon表示其数值,而其他因子中则表示其指数的大小。
求导规则通过抽象类来实现,规定好统一的接口,在各个因子中实现。
Factors类就是项的概念——多个因子相乘得到的数据类型。并且项的求导规则可以直接调用下面各个因子的求导规则并且添加新的项来实现。
Term类是Factors聚合而成的,其本质是项的聚合,所以具有表达式的作用,但是其内部功能只有输出和求导合并三个方法。
Expr类是输入输出类,主要对输入数据进行递归处理,输出时对输出的内容进行递归处理输出。
经过重构各个类的功能都变得十分清晰,这样非常方便添加新的功能——括号嵌套。括号嵌套的在本次作业中通过"挂载数据"的方式来实现(其本质还是递归处理问题),所以在sin(x) 这些因子类中声明表达式,如果有嵌套,则将嵌套的内容存储到表达式实例中。 这样无论是求导还是输出输入都可以递归向下进行,十分方便。
设计模式
本单元作业最终采用的是工厂模式,四种因子可以视为工厂生产的四种产品,具体的内容由输入来决定实例化哪一个因子。并且生产方法——求导方法,通过接口来实现,这样就比较便捷的管理整个程序的类关系。
程序bug检验
对于程序中的bug检测,首先要立足于对需求的深刻理解,在本三次作业中,搞清楚哪些是WRONG FORMAT至关重要。虽然没有互测环节,但是我们还是尽量对自己的程序尽可能多的测试。
Bug检验是一个由简单到复杂的过程:1.单个因子检查 -> 2.单个项的检查 -> 3.表达式的检查 ->4.含有特殊规则的表达式检查->5.脚本生成数据进行检查
单个因子的检查
对于前三次作业单个因子的检查都是比较容易枚举来实现的,重点是枚举因子的特殊情况,如-x, sin(x)^0,该类含有特殊省略规则的情况。
单个项的检查
同样的检查重点在于两部分,(1)因子之间组合成项(2)项自身具有的特殊情况,如1*x 省略为 x, +1*+1 省略为++1等
表达式的检查
同上,检查重点在于表达式本身的特殊情况,同时应该注意一些不符合输入规范的样例。
特殊规则检查
在表达式的层面,对特殊情况进行归纳,然后一一检查各类特殊情况,如第二次作业的 +++1 和++++1 分别为合法输入和不合法输入,又如进行压力测试(输入长字符串)和边界条件(超出long 的数据范围)测试。
脚本生成数据检查
- 使用python脚本,使用xeger 按照相应的正则表达式进行生成数据,这一步重点在于确认需求理解无误和正则表达式的正确性。
- 使用sympy 包设置符号求导
- 将标准答案和Java计算出的答案带入随机数据进行比较
使用脚本进行检查,可以得到大量的测试数据。但是前四个步骤完成之后程序中主要的bug已经被修复了,所以最后一步往往是最终测试的确认,排除会偶然发生的错误。
在前四个步骤进行测试的时候,可以使用 run "Project name" with coverage,这样可以看到哪些行被检测到了,哪些部分还没有被测试到,更有针对性的进行检查。比如下图为第三次作业输入某个样例后的代码覆盖情况,可以看出Constant类被全部覆盖到,而Sinx类只有70%的覆盖率,可以点击Line到类中具体查看哪些代码没有被覆盖,并且构造相应的输入样例覆盖需要测试的代码段。
基于度量的程序结构分析
程序结构图
首先给出第三次作业的结构图: 可以看出Varx (表示括号内的部分)和 Constant(表示常数)这两个类被其他因子类所使用,而Sinx和Cosx之间相互的关系仅仅是求导产生的对偶关系。
term 作为存储表达式的类,其和各个类均保持密切的联系。而expr类作为主要处理输入输出的类别其仅仅和项(factors类)有联系,并不会和factor类(Sinx Cosx Varx)产生直接联系,降低了程序的复杂度和产生bug的概率。
下面给出一些程序的数据分析。
第一次作业
类的相关统计数据
LOCM表示耦合程度,期望其值低;FANIN表示内聚程度,所以期望FANIN的值要高。
方法度量
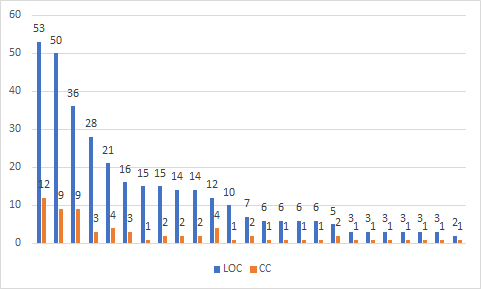
LOC表示代码行数,CC表示循环,PC表示方法的参数
可以看出大部分方法行数较短,几个主要的方法行数比较长,这是比较符合常规的。
第二次作业
类的相关统计数据
方法度量
第三次作业
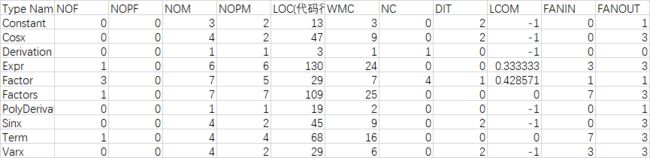
类的相关数据统计
代码异味
通过分析看出在out 函数中使用了大量的神仙数(没有明确标明意义的常数),这个在以后的作业中需要修正。
以及比较复杂的条件和比较复杂的方法,这些都是需要进一步重构的方法。
方法度量
总结
通过本单元的作业基本了解了面向对象数据抽象等基础思想,并且熟悉了Java正则表达式的使用,也积累了一些重构的工程经验。
最后使用相关工具进行分析时仍能看出代码中不少部分具有的问题,所以在以后的工程实践中仍需要增加分析代码完善代码这一迭代环节。
不足之处是,在重构代码和添加新功能时,没有能够较为熟练的应用设计模式,所有内容都在自己脑子中架构,所以在下一单元的作业里面,希望能够有意识的应用设计模式。