HDU 5725 2016多校Contest 1 C题【gets比getchar更快!!思维题】
题目大意:
给一个n*m的棋盘,然后有很多棋子,这些棋子不能“8相邻”,也不能在同一行同一列上。
然后问,剩下的棋盘的格子,合法配对中,两两配对的最短距离的和,除以配对的对数。
配对对数好算,两两配对的最短距离的和,比较难算。
题目要求出所有合法点对间的最短路径的平均值,因此我们应当求出所有合法最短点对的最 短路径之和,再除以合法点对个数。 题目中Guard之间有着很不自然的制约关系,每个Guard的周围和同行、列都不能有其余的 Guard,但不可路过的格子却只有本身一格。由此发现,任意两点间的最短路径只会至多被 一个Guard所干扰。 因此可以想到,我们可以先算出没有Guard制约的所有最短路径长度之和,再分别对于每个 Guard求出它对最短路径长度的贡献(即原本必须经过它的最短路要多绕两格)。
官方题解说的一知半解,不太看的懂。。后来看了一个大牛的博客http://blog.csdn.net/u013849646/article/details/52004910分析他的代码看懂怎么捉了。。。
首先,可以先求出来所有可以配对的点,他们两两之间的距离和。 这可以先从x方向,y方向分别考虑。(感觉好厉害啊。。完全没想到可以这么算)。
也就是说,第a行有q个空,第b行,有p个空格。 那么这两行之间所有棋子的距离在y坐标上和为 abs(a-b)*p*q。 先统计所有y坐标,再统计x坐标同样的方法就行了。
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= n; ++ j)
ans += x[i] * x[j] * abs(i - j);
for (int i = 1; i <= m; ++ i)
for (int j = 1; j <= m; ++ j)
ans += y[i] * y[j] * abs(i - j);ans即为所有图里的点配对距离总和。
但是还未考虑被棋子阻隔的情况。
然后开始考虑棋子干扰的问题。根据题解(和意淫,和自己画图……)可以得出,2点最短路,只可能被一个棋子阻隔,或者不被阻隔。
阻隔的情况如下:
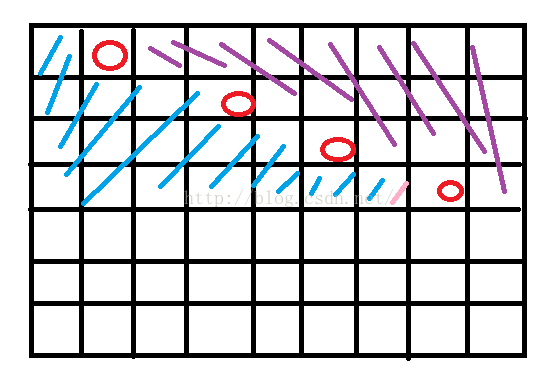
左边蓝色阴影部分,到紫色阴影部分,其中的一些情况会被阻隔。。。(自己画图画几个例子)
也就是说,一旦棋子是单调下降的,那么左边到右边对应的地方就会被阻隔。 比如左边第一行,到右边第1、2、3、4行都被阻隔。 左边第二行,到右边2,3,4行会被阻隔。
同理,棋子单调升也是类似的情况。(要注意去重!! 但是这个比较好写)
然后。。。就解决了。
超时的话:读入用gets,getchar超时。
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
int n, m;
const int maxn = 1010;
char s[maxn][maxn];
void init()
{
scanf("%d%d", &n, &m);
getchar();//吃一个回车
for (int i = 1; i <= n; ++ i)
{
gets(s[i] + 1);
/*
for (int j = 1; j <= m; ++ j)
s[i][j] = getchar();
getchar();//吃一个回车
*/
}
}
int x[maxn], y[maxn], gx[maxn], gy[maxn];
inline int abs(int a)
{
if (a<0) return -a;
return a;
}
LL ans;
void f(int n, int m, int a[])
{
LL sum = 0;
for (int i = 1; i <= n; ++ i)
{
if (a[i] > a[i - 1]) sum += a[i] - 1;
else if (a[i] == 0) sum = 0;
else sum = a[i] - 1;
ans += 4LL * sum * (m - a[i]);
}
}
void g(int n, int m, int a[])
{
LL sum = 0;
for (int i = n; i >= 1; -- i)
{
if (a[i] < a[i + 1]) sum = 0;
ans += 4LL * sum * (m - a[i]);
if (a[i] > a[i + 1]) sum += a[i] - 1;
else if (a[i] == 0) sum = 0;
else sum = a[i] - 1;
}
}
void doit()
{
ans = 0;
int tot = 0;
memset(x, 0, sizeof(x));
memset(y, 0, sizeof(y));
memset(gx, 0, sizeof(gx));
memset(gy, 0, sizeof(gy));
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= m; ++ j)
{
if (s[i][j] == 'G')
{
gx[i] = j;
gy[j] = i;
}
else
{
++x[i];
++y[j];
++ tot;
}
}
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= n; ++ j)
ans += x[i] * x[j] * abs(i - j);
for (int i = 1; i <= m; ++ i)
for (int j = 1; j <= m; ++ j)
ans += y[i] * y[j] * abs(i - j);
// for (int i = 1; i <= n; ++ i) cout<