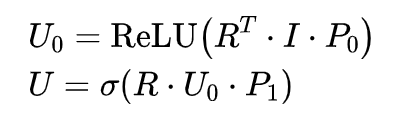图自编码器的起源和应用

©PaperWeekly 原创 · 作者｜刘昊东

学校｜电子科技大学硕士生

研究方向｜推荐系统，表示学习

Kipf 与 Welling 16 年发表的「Variational Graph Auto-Encoders」提出了基于图的（变分）自编码器 Variational Graph Auto-Encoder（VGAE），自此开始，图自编码器凭借其简洁的 encoder-decoder 结构和高效的 encode 能力，在很多领域都派上了用场。

本文将先详尽分析最早提出图自编码器的「Variational Graph Auto-Encoders」这篇论文，将从以下几个角度进行分析：

• VGAE 的思想 

• 没有变分阶段的 GAE 的 encoder、decoder 阶段 

• 有变分阶段的 VGAE 

• 如何从确定分布再到从分布中采样 

• 实验效果分析

然后会再介绍两篇关于如何应用图自编码器的文章。

Variational Graph Auto-Encoders

论文标题：Variational Graph Auto-Encoders

论文来源：NIPS 2016

论文链接：https://arxiv.org/abs/1611.07308

1.1 论文概览

先简单描述一下图自编码器的 intention 和用途：获取合适的 embedding 来表示图中的节点不是容易的事，而如果能找到合适的 embedding，就能将它们用在其他任务中。VGAE 通过 encoder-decoder 的结构可以获取到图中节点的 embedding，来支持接下来的任务，如链接预测等。

VGAE 的思想和变分自编码器（VAE）很像：利用隐变量（latent variables），让模型学习出一些分布（distribution），再从这些分布中采样得到 latent representations（或者说 embedding），这个过程是 encode 阶段。

然后再利用得到的 latent representations 重构（reconstruct）出原始的图，这个过程是 decode 阶段。只不过，VGAE 的 encoder 使用了 GCN，decoder 是简单的内积（inner product）形式。

下面具体讲解变分图自编码器（VGAE）。先讲 GAE，即图自编码器（没有变分）。

1.2 图自编码器（GAE）

统一规范，规定几个 notation 如下：

• 图用   表示，其中   表示节点集合，  表示边集合

• : 邻接矩阵

• : 度矩阵

• : 节点数

• : 节点的特征（features）维度

• 表示节点的特征矩阵

• : embedding 维度

• : 节点的 embedding

1.2.1 Encoder

GAE 使用 GCN 作为 encoder，来得到节点的 latent representations（或者说 embedding），这个过程可用一行简短的公式表达：

将 GCN 视为一个函数，然后将   和   作为输入，输入到 GCN 这个函数中，输出  ，  代表的就是所有节点的 latent representations，或者说 embedding。

如何定义 GCN 这个函数？kipf 在论文中定义如下：

其中， ，  和   是待学习的参数。

简言之，这里 GCN 就相当于一个以节点特征和邻接矩阵为输入、以节点 embedding 为输出的函数，目的只是为了得到 embedding。

1.2.2 Decoder

GAE 采用 inner-product 作为 decoder 来重构（reconstruct）原始的图：

上式中，  就是重构（reconstruct）出来的邻接矩阵。

1.2.3 How to learn

一个好的 Z，就应该使重构出的邻接矩阵与原始的邻接矩阵尽可能的相似，因为邻接矩阵决定了图的结构。因此，GAE 在训练过程中，采用交叉熵作为损失函数：

上式中，  代表邻接矩阵   中某个元素的值（0 或 1），  代表重构的邻接矩阵   中相应元素的值（0 到 1 之间）。

从损失函数可以看出来，希望重构的邻接矩阵（或者说重构的图），与原始的邻接矩阵（或者说原始的图）越接近、越相似越好。

1.2.4 小结

图自编码器（GAE）的原理简明、清晰，训练起来不麻烦，因为可训练的参数只有   和  ，kipf 的代码实现中，这两个参数矩阵的维度分别是   和  ，如果  ，也只有 32512 个参数，相当少了。

下面是 VGAE（变分图自编码器）。

1.3 变分图自编码器（VGAE）

在 GAE 中，一旦 GCN 中的   和   确定了，那么 GCN 就是一个确定的函数，给定   和  ，输出的   就是确定的。

而在 VGAE 中，  不再由一个确定的函数得到，而是从一个（多维）高斯分布中采样得到，说得更明确些，就是先通过 GCN 确定一个（多维）高斯分布，再从这个分布中采样得到  。下面简单描述一下这个过程。

1.3.1 确定均值和方差

高斯分布可以唯一地由二阶矩确定。因此，想要确定一个高斯分布，只需要知道均值和方差。VGAE 利用 GCN 来分别计算均值和方差：

这里有两个要注意的地方，第一个是 GCN 的下标，  和   中的   是相同的、共享的，但   是不同的，因此用下标来作区分；第二个是通过   得到的是  ，这样可以方便后续的计算。

1.3.2 采样

既然已经得到了均值和方差（准确来说应该是均值向量和协方差矩阵），就可以通过采样得到   了，但是，采样操作无法提供梯度信息，也就是说，反向传播在采样操作无法计算梯度，也就无法更新   和  。解决办法是重参数化（reparameterization）。

简单说一下重参数化。如果   服从  ，那么   就服从  。因此，可以先从标准高斯中采样一个  ，再通过   计算出  ，这样一来，  的表达式清晰可见，梯度信息也就有了。

VGAE 的 decoder 也是一个简单的 inner-product，与 GAE 的 decoder 没有区别。

1.3.3 How to learn

VGAE 依然希望重构出的图和原始的图尽可能相似，除此之外，还希望   计算出的分布与标准高斯尽可能相似。因此损失函数由交叉熵和 KL 散度两部分构成：

其中，  是 GCN 计算出的分布，  是标准高斯。

不过，论文中的优化目标是这样的：

这是用变分下界写出的优化目标，第一项是期望，第二项是 KL 散度。

1.4 效果分析

Kipf 和 Welling 在三个数据集上进行了效果分析，任务是链接预测，详情见下表：

可见，（变分）图自编码器在三个数据集上的效果都很好，不过，注意带星号的 GAE* 和 VGAE*，这两个模型是不带 input features 的，就是说节点的 features 就是 one-hot 向量，这种情况下，（变分）图自编码器的效果不仅不比 SC 和 DW 好，甚至还有点差。

不过，Kipf 和 Welling 在论文中指出，SC 和 DW 不支持 input features，因此能够使用 input features 是 VGAE 的特点之一。

以上是对图自编码器的开山论文 Variational Graph Auto-Encoders 的介绍，接下来看看图自编码器在最近两年的一些应用。

Graph Convolution Matrix Completion

论文标题：Graph Convolution Matrix Completion

论文来源：KDD 2018

论文链接：https://www.kdd.org/kdd2018/files/deep-learning-day/DLDay18_paper_32.pdf

2.1 论文概览

这是 Kipf 作为二作的一篇解决推荐系统中 matrix completion 问题的文章，发表在 18 年的 KDD。

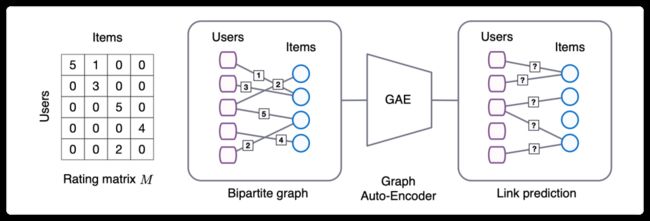
这篇文章提出，matrix completion 任务可以视作为 graph 上的链接预测问题，即 users 和 items 构成了一张二部图，图上的边代表相应的 user 与 item 进行了交互，于是 matrix completion 问题就变成了预测这张二部图上的边的问题。

为了解决 users-items 二部图上的链接预测问题，这篇文章提出了基于在二部图上进行 message passing 的图自编码器框架 GCMC，且引入了 side information，还分析了 side information 对于推荐系统中冷启动的影响。

2.2 模型详解

先简要分析一下 GCMC 的整体框架。首先，GCMC 把 users 和 items 的初始 features  和   （one-hot 向量）输入到一个 GCN 层中，得到 users 和 items 的 hidden representations:  ,  ，再将 users 和 items 的 side information   和   输入到一个 Dense 层中，得到 side information 的 hidden representations:  ,  。

然后将初始 features 和 side information 的 hidden representations 一起输入到一个 Dense 层中，得到 users 和 items 最终的 embeddings:  ,  （以上为 encoder 阶段），最后通过计算内积（decoder 阶段），预测 user 对 item 的喜好程度。

下面给出每一步的详细计算方法。

首先，GCN 层的计算方式如下：

其中，  是 item j 传递给 user i 的信息，下标 r 指定了 user i 给 item j 的评分是 r（由于用户的评分类别不止一种，因此使用不同的 r 来区分，即  ）。

 是参数矩阵，  是归一化因子，可以是   或者  ，其中   表示 user i 的邻居数。accum 也有两种选择：stack 或者 sum。  表示激活函数，可以是 sigmoid、ReLU 等。

得到了 user i 的初始 feature 的 hidden representation   后，再将 side information 的 hidden representation 与   一起输入进一个 Dense 层即可得到 user i 的最终 embedding：

其中，右式表示得到 side information 的 hidden representation 的 Dense 层，左式表示得到最终 embedding 的 Dense 层。

在得到 users 和 items 的 embeddings 后，通过下式来预测 user i 对 item j 的评分属于 r 的概率：

最终，GCMC 对 user i 对 item j 的评分的预测为：

2.3 效果分析

作者使用了 6 个数据集，可以分为 3 类：

• 对比的方法只利用 users 或 items 一方的 features：ml-100k

• GCMC 和 对比的方法都不使用 side information：ml-1m，ml-10m

• Users 和 items 的 side information 以 graph 的形式呈现：Flixster，Douban，YahooMusic

实验结果：

实验结果表明，在有 side information 时，GCMC 的效果好于其他方法，尤其是当 side information 以 graph 的形式存在时，GCMC 的效果优势更加明显。而当没有 side information 时，GCMC 也表现出了 competitive results。

作者还分析了 side information 对冷启动的影响，文中以 ml-100k 为例，将一些用户的评分数量人为减少，然后对比了 GCMC 分别在使用和不使用 side information 时的效果。

从上图可以看出，使用 side information 的 GCMC 效果更好，而且随着冷启动用户的人数增多，引入 side information 带来的效果提升更加明显。

2.4 小结

该篇论文将推荐系统中的 matrix completion 任务视作 graph 上的链接预测任务来处理，并使用图自编码器，引入 side information，在一些 benchmark 数据集上超过了一些 SOTA 方法，而且还分析了 side information 给冷启动带来的帮助。

GraphCAR

论文标题：GraphCAR: Content-aware Multimedia Recommendation with Graph Autoencoder

论文来源：SIGIR 2018

论文链接：https://dl.acm.org/doi/10.1145/3209978.3210117

3.1 论文概览

上一篇论文中，GCMC 的目标是解决 matrix completion 问题，即预测 user 对 item 的评分是多少。这篇文章要解决的问题可以归类为推荐系统中 top-n 推荐问题，即给用户推荐 n 个 ta 可能最感兴趣的 items。

这篇文章指出，用户在选择图片或者视频时，图片或视频本身的 multimedia content 是最重要的因素，但已有的一些方法没能对 multimedia content 给予足够的重视，

因此，基于 GAE 的思想，该文章提出了 GraphCAR 模型，除了 users 和 items 之间的交互数据，该模型还利用了 users 的 attributes 和 items 的 multimedia content。

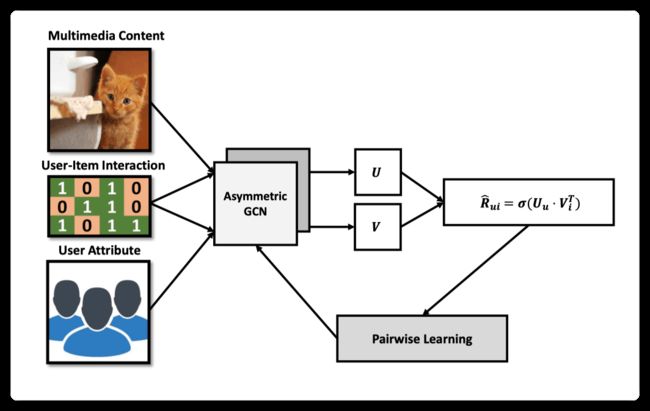
3.2 模型详解

GraphCAR 的整体框架基本遵循着 GAE 的框架，即先使用 GCN 获取 users 和 items 的 embeddings，然后使用内积来预测 user 对 item 的偏好评分。

首先，在 GCN 阶段（即 encoder 阶段），为了获取 users 的 embedding，GCN 使用 user-item 的交互矩阵   和 users 的 attributes 矩阵   作为输入，然后输出 users 的 embeddings 矩阵  ：

其中   是参数矩阵。对于 items 的 embeddings，只需要将 users attributes 矩阵换成 items 的 feature 矩阵   即可（  即为 multimedia content）：

得到 embeddings 之后，便可利用内积形式的 decoder 计算出预测的 preferences:  。

由于 GraphCAR 要解决的是 top-n 推荐问题，因此目标函数选择了 BPR pairwise 目标，即：

和 GCMC 的不同之处在于，GraphCAR 直接对 users 和 items 的 interactions 和 side information 一起建模，而不是像 GCMC 中那样，先分别得到初始 features（one-hot 向量）和 side information 的 hidden representations，然后再得到最终的 embeddings。

对比下来，GraphCAR 的方式更直接，但貌似这种方法只能在有 users 和 items 的 side information 的情况下才能生效。

3.3 效果分析

论文在 Amazon 和 Vine 两个数据集上进行了实验，其中 Amazon 提供了 image features，Vine 提供了 video features。实验结果如下：

另外，作者还分析了 users 交互过的 items 的数量对 GraphCAR 的影响：

从图中可以看出，GraphCAR 对于交互数量较少的 users 的效果优势并不明显，而当 users 的交互数量增多时，效果优势开始慢慢明显起来。

3.4 小结

这篇论文要解决的问题是推荐系统中 top-n 推荐的问题，在分析发现以往的方法并没有充分利用 items 本身的 multimedia content 后，该论文采取了直接用 GCN 对 user-item interactions 和 side information 建模的方式来得到 embeddings，随之而来的问题是，如果不存在 users attributes 或 items multimedia content 可利用，GraphCAR 可能需要改变一些处理的方式。

总结

图自编码器最开始是以变分图自编码器的形式提出的，但近两年基本上都应用的是没有变分阶段的图自编码器。

GAE 的形式很简洁，首先通过 GCN 得到图中节点的 embeddings（encoder 阶段），然后再根据具体任务重构出原始的图的特点（decoder 阶段）。

从以上三篇文章可以看出，decoder 阶段都采取的是两层 GCN 结构，而 decoder 阶段都采取的是 inner-product 结构，可以看出，也许结构上还有改进的空间，而不是仅限于两层 GCN 或者简单的内积形式。

点击以下标题查看更多往期内容： 

• 变分推断（Variational Inference）最新进展简述
  

• 变分自编码器VAE：原来是这么一回事
  

• 图神经网络三剑客：GCN、GAT与GraphSAGE
  

• 如何快速理解马尔科夫链蒙特卡洛法？
  

• 深度学习预训练模型可解释性概览
  

• ICLR 2020：从去噪自编码器到生成模型

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

???? 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

???? 投稿邮箱：

• 投稿邮箱：[email protected] 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

????

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。