pyimagesearch-4 聪明的女孩:计算机视觉和图像搜索引擎使用颜色直方图的指南
It’s…it’s a histogram. – Dr. Grant
好吧,也许这不是确切的引用。但是,如果格兰特博士知道颜色直方图的力量,我认为他会同样激动。
更重要的是,当电力耗尽时,直方图不会让游客吃东西。
那么,直方图到底是什么?直方图表示图像中颜色的分布。它可以被视为图形(或图),给出了强度(像素值)分布的高级直觉。在此示例中,我们将假设RGB颜色空间,因此这些像素值将在0到255的范围内。如果您在不同的颜色空间中工作,则像素范围可能不同。
绘制直方图时,X轴作为我们的“箱”bin不知道怎么翻译。。。如果我们构造一个256个二进制位的直方图,那么我们有效地计算每个像素值出现的次数。相反,如果我们仅使用2个(等间距)分档,那么我们计算像素在[0,128]或[128,255]范围内的次数。然后,在Y轴上绘制分箱到X轴值的像素数。
OpenCV和Python版本:此示例将在Python 2.7和OpenCV 2.4.X / OpenCV 3.0+上运行。
通过简单地检查图像的直方图,您可以大致了解对比度,亮度和强度分布。这篇文章将从头到尾为您提供OpenCV直方图示例。
应用于图像搜索引擎
在图像搜索引擎的中,直方图可以用作特征向量(即,用于量化图像并将其与其他图像进行比较的数字列表)。为了在图像搜索引擎中使用颜色直方图,我们假设具有相似颜色分布的图像在语义上相似。我将在本文后面的“缺点”一节中详细讨论这个假设;但是,暂时让我们继续并假设具有相似颜色分布的图像具有相似的内容。
可以使用距离度量来比较颜色直方图的“相似性”。常见的选择包括:欧几里得,相关,卡方,交点和巴氏距离(Euclidean, correlation, Chi-squared, intersection, and Bhattacharyya)。在大多数情况下,我倾向于使用卡方距离,但选择通常取决于被分析的图像数据集。无论您使用哪种距离指标,我们都将使用OpenCV来提取我们的颜色直方图。
游览侏罗纪公园
让我们想象一下,我们和格兰特博士以及公司一起参加了他们的第一次侏罗纪公园之旅。我们携带手机记录了整个体验(并且让我们假装拍照手机是当时的“事物”)。假设我们没有让Dennis Nedry让我们的脸被Dilophosaurus吃掉,我们以后可以将智能手机中的图片下载到我们的计算机上并计算每个图像的直方图。
在游览的最初阶段,我们在实验室中花了很多时间,学习DNA并亲眼目睹婴儿龙的孵化。这些实验室有很多“钢”和“灰色”颜色。后来,我们乘坐吉普车开进了公园。公园本身就是一个丛林 - 很多绿色。
所以基于这两种颜色分布,您认为上面的Dr. Grant图像和哪一个更相似?
好吧,我们看到照片背景中有相当数量的绿化。在所有可能性中,格兰特博士照片的颜色分布与我们在丛林旅行期间拍摄的照片与实验室拍摄的照片更为“相似”。
使用OpenCV计算直方图
现在,让我们开始构建我们自己的一些颜色直方图。我们将在OpenCV中使用cv2.calcHist函数来构建直方图。在我们进入任何代码示例之前,让我们快速回顾一下这个函数:cv2.calcHist(images, channels, mask, histSize, ranges)
- images:这是我们想要计算直方图的图像。将其包装为列表:[myImage]。
- channels:索引列表,我们在其中指定要为其计算直方图的通道的索引。要计算灰度图像的直方图,列表将为[0]。要计算所有三个红色,绿色和蓝色通道的直方图,通道列表将为[0,1,2]。
- mask:我还没有在这个博客中覆盖过遮蔽,但实际上,遮罩是一个与原始图像具有相同形状的
uint8图像,其中忽略值为零的像素,值大于零的像素为包括在直方图计算中。使用掩码允许我们仅计算图像的特定区域的直方图。现在,我们只使用None值作为掩码。 - histSize:这是我们在计算直方图时要使用的bin数。同样,这是一个列表,我们正在为每个通道计算一个直方图。bin尺寸并非都必须相同。以下是每个通道的32个箱的示例:[32,32,32]。
- ranges:可能的像素值范围。通常,对于每个通道,这是[0,256],但如果使用RGB以外的颜色空间(例如HSV),则范围可能不同。
现在我们已经了解了cv2.calcHist函数,让我们编写一些实际的代码。
# import the necessary packages
from matplotlib import pyplot as plt
import numpy as np
import argparse
import cv2
# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-i", "--image", required = True, help = "Path to the image")
args = vars(ap.parse_args())
# load the image and show it
image = cv2.imread(args["image"])
cv2.imshow("image", image)
这段代码还不是很令人兴奋。我们所做的只是导入我们需要的包,设置参数解析器,以及加载我们的图像。
# convert the image to grayscale and create a histogram
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
cv2.imshow("gray", gray)
hist = cv2.calcHist([gray], [0], None, [256], [0, 256])
plt.figure()
plt.title("Grayscale Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
plt.plot(hist)
plt.xlim([0, 256])
现在事情变得更有趣了。在第2行,我们将图像从RGB颜色空间转换为灰度。第4行计算实际直方图。继续并将代码的参数与上面的函数文档相匹配。我们可以看到我们的第一个参数是灰度图像。灰度图像只有一个通道,因此通道的使用值为[0]。我们没有掩码,因此我们将掩码值设置为None。我们将在直方图中使用256个bin,可能的值范围为0到256。
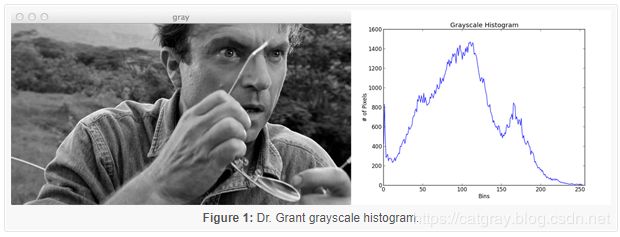
还不错。我们如何解释这个直方图?好吧,bin(0-255)绘制在X轴上。并且Y轴计算每个bin中的像素数。大多数像素落在50到125的范围内。查看直方图的右尾,我们看到200到255范围内的像素非常少。这意味着图像中的“白色”像素非常少。
现在我们已经在灰度直方图上看到了,让我们看看我称之为“扁平”的颜色直方图:
# grab the image channels, initialize the tuple of colors,
# the figure and the flattened feature vector
chans = cv2.split(image)
colors = ("b", "g", "r")
plt.figure()
plt.title("'Flattened' Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
features = []
# loop over the image channels
for (chan, color) in zip(chans, colors):
# create a histogram for the current channel and
# concatenate the resulting histograms for each
# channel
hist = cv2.calcHist([chan], [0], None, [256], [0, 256])
features.extend(hist)
# plot the histogram
plt.plot(hist, color = color)
plt.xlim([0, 256])
# here we are simply showing the dimensionality of the
# flattened color histogram 256 bins for each channel
# x 3 channels = 768 total values -- in practice, we would
# normally not use 256 bins for each channel, a choice
# between 32-96 bins are normally used, but this tends
# to be application dependent
print "flattened feature vector size: %d" % (np.array(features).flatten().shape)
计算扁平颜色直方图与灰度直方图相比,肯定有更多代码。让我们拆开这段代码,更好地理解正在发生的事情:
- 第3-4行:我们要做的第一件事是将图像分成三个通道:蓝色,绿色和红色。通常,我们读到这是一个红色,绿色,蓝色(RGB)。但是,OpenCV以相反的顺序将图像存储为NumPy数组:BGR。这一点很重要。然后我们初始化一个代表颜色的字符串元组。
- 第5-9行:这里我们只是设置我们的PyPlot图并初始化我们的连接直方图列表。
- 第12行:让我们开始遍历通道。
- 第16-17行:我们现在计算每个通道的直方图。实质上,这与计算单个通道灰度图像的直方图相同。然后,我们将颜色直方图连接到我们的特征列表。
- 第20行:使用当前通道名称绘制直方图。
- 第29行:这里我们只是检查我们的扁平颜色直方图的形状。我将其称为“扁平”直方图,不是因为(1)直方图具有零“峰值”或(2)我称之为NumPy的flatten()方法。我称之为“扁平”直方图,因为直方图是一个像素计数列表。之后,我们将探索多维直方图(2D和3D)。扁平直方图只是连接在一起的每个单独通道的直方图。
现在让我们绘制颜色直方图:

真棒。这很简单。这个直方图告诉我们什么?嗯,bin#50周围的深蓝色像素值有一个峰值。这一系列的蓝色指的是格兰特的蓝色衬衫。从#50到#125的更大范围的绿色像素指的是格兰特博士背后的森林。
多维直方图
到目前为止,我们一次只计算了一个通道的直方图。现在我们继续进行多维直方图,并一次考虑两个通道。
我喜欢解释多维直方图的方法是使用单词 AND。例如,我们可以提出一个问题,例如“有多少像素的红色值为10 AND 蓝色值为30?”有多少像素的绿色值为200 AND 红色值为130?通过使用连接 AND,我们能够构建多维直方图。就这么简单。
让我们检查一些代码以自动化构建2D直方图的过程:
# let's move on to 2D histograms -- I am reducing the
# number of bins in the histogram from 256 to 32 so we
# can better visualize the results
fig = plt.figure()
# plot a 2D color histogram for green and blue
ax = fig.add_subplot(131)
hist = cv2.calcHist([chans[1], chans[0]], [0, 1], None,
[32, 32], [0, 256, 0, 256])
p = ax.imshow(hist, interpolation = "nearest")
ax.set_title("2D Color Histogram for Green and Blue")
plt.colorbar(p)
# plot a 2D color histogram for green and red
ax = fig.add_subplot(132)
hist = cv2.calcHist([chans[1], chans[2]], [0, 1], None,
[32, 32], [0, 256, 0, 256])
p = ax.imshow(hist, interpolation = "nearest")
ax.set_title("2D Color Histogram for Green and Red")
plt.colorbar(p)
# plot a 2D color histogram for blue and red
ax = fig.add_subplot(133)
hist = cv2.calcHist([chans[0], chans[2]], [0, 1], None,
[32, 32], [0, 256, 0, 256])
p = ax.imshow(hist, interpolation = "nearest")
ax.set_title("2D Color Histogram for Blue and Red")
plt.colorbar(p)
# finally, let's examine the dimensionality of one of
# the 2D histograms
print "2D histogram shape: %s, with %d values" % (
hist.shape, hist.flatten().shape[0])
是的,这是相当多的代码。但这仅仅是因为我们正在为RGB通道的每个组合计算2D颜色直方图:红色和绿色,红色和蓝色,以及绿色和蓝色。
现在我们正在使用多维直方图,我们需要记住我们正在使用的垃圾箱数量。在前面的例子中,我使用256个bin来进行演示。但是,如果我们在2D直方图中为每个维度使用256个二进制位,则我们得到的直方图将具有65,536个单独的像素计数。这不仅浪费资源,而且不实用。大多数应用程序在计算多维直方图时使用8到64个区间。正如第8-9行所示,我现在使用的是32个而不是256个。
通过检查cv2.calcHist函数的第一个参数,可以看出最重要的代码。在这里,我们看到我们传递了两个频道的列表:绿色和蓝色频道。这就是它的全部内容。
那么如何在OpenCV中存储2D直方图?这是一个2D NumPy数组。由于我为每个通道使用了32个bin,我现在有一个32×32的直方图。我们可以简单地通过展平它来将此直方图视为特征向量(第33行)。展平我们的直方图会产生一个包含1024个值的列表。
我们如何可视化2D直方图?让我们来看看。

在上图中,我们看到三个图。第一个是绿色和蓝色通道的2D颜色直方图,第二个是绿色和红色,第三个是蓝色和红色。蓝色阴影表示低像素计数,而红色阴影表示大像素计数(即2D直方图中的峰值)。当X = 5且Y = 10时,我们可以在绿色和蓝色2D直方图(第一个图)中看到这样的峰值。
使用2D直方图一次考虑两个通道。但是,如果我们想要考虑所有三个RGB通道呢?你猜到了。我们现在要构建一个3D直方图。
# our 2D histogram could only take into account 2 out
# of the 3 channels in the image so now let's build a
# 3D color histogram (utilizing all channels) with 8 bins
# in each direction -- we can't plot the 3D histogram, but
# the theory is exactly like that of a 2D histogram, so
# we'll just show the shape of the histogram
hist = cv2.calcHist([image], [0, 1, 2],
None, [8, 8, 8], [0, 256, 0, 256, 0, 256])
print "3D histogram shape: %s, with %d values" % (
hist.shape, hist.flatten().shape[0])
这里的代码非常简单 - 它只是上面代码的扩展。我们现在为每个RGB通道计算8x8x8直方图。我们无法想象这个直方图,但我们可以看到形状确实是(8,8,8),有512个值。同样,将3D直方图视为特征向量可以通过简单地展平阵列来完成。
颜色空间
本文中的示例仅探讨了RGB颜色空间,但可以为OpenCV中的任何颜色空间构建直方图。讨论色彩空间不在本文的上下文中,但如果您有兴趣,请查看有关转换色彩空间的文档。
不足
在这篇文章的早些时候,我们假设具有相似颜色分布的图像在语义上相似。对于小而简单的数据集,事实上这可能是真的。然而,在实践中,这种假设并不总是成立。
让我们思考下为什么会这样。
例如,颜色直方图根据定义忽略图像中对象的形状和纹理。这意味着颜色直方图没有对象形状或对象纹理的概念。此外,直方图还忽略任何空间信息(即图像中像素值来自何处)。直方图的扩展(颜色相关图)可用于编码像素之间的空间关系。
让我们来看看我的视觉时尚搜索引擎iPhone应用程序Chic Engine。我对不同类型的衣服有不同的类别,比如鞋子和衬衫。如果我使用颜色直方图来描述红色鞋子和红色衬衫,直方图将假设它们是相同的对象。显然它们都是红色的,但语义结束了 - 它们根本就不一样了。颜色直方图根本无法“塑造”鞋子或衬衫的样子。
最后,颜色直方图对“噪声”敏感,例如捕获图像的环境中的光照变化和量化误差(选择要增加的箱子)。通过使用与RGB不同的颜色空间(例如HSV或L*a*b*),可以减轻这些限制中的一些。
然而,尽管如此,直方图仍然被广泛用作图像描述符。它们易于实现且计算速度非常快。虽然它们有其局限性,但如果在正确的环境中使用它们,它们会非常强大。
下一步做什么?
在这篇文章中,我从头到尾提供了一个使用Python的OpenCV直方图示例。下一步,我们将使用颜色直方图从前到后构建我们的第一个图像搜索引擎。你兴奋吗?我反正是。也许我会切换整个侏罗纪公园主题,这些主题一直在这里建立起来。虽然没有保证。
