【实习】机器学习相关知识

【实习】机器学习相关知识

---

ROC，AUC，Precision，Recall，F1的介绍与计算

真阳性（TP）：判断为真，实际为真。
伪阳性（FP）：判断为真，实际为假。
真阴性（TN）：判断为假，实际为假。
伪阴性（FN）：判断为假，实际为真。

精确率/查准率（precision）：预测为真，实际也为真，占所有预测为真的比例的大小。精确率是针对我们预测结果而言的
precision=TPTP+FP p r e c i s i o n = T P T P + F P
召回率/查全率（recall）：预测为真，实际为真，占所有样本为真的比例的大小。召回率是针对样本而言的。
recall=TPTP+FN r e c a l l = T P T P + F N

两者取值在0和1之间，数值越接近1，查准率或查全率就越高。

F值是综合两者进行评估，反映整体指标。因为P和R两者在某些情况下是矛盾的。
F=2RPR+P F = 2 R P R + P

ROC（Receiver Operating Characteristic），其主要分析工具是一个画在二维平面上的曲线——ROC curve。平面的横坐标是false positive rate(FPR)，纵坐标是true positive rate(TPR)。
真正类率(true positive rate ,TPR),刻画的是分类器所识别出的正实例占所有正实例的比例。
TPR=TP(TP+FN) T P R = T P ( T P + F N )
负正类率(false positive rate, FPR),计算的是分类器错认为正类的负实例占所有负实例的比例。
FPR=FP(FP+TN) F P R = F P ( F P + T N )
还有一个真负类率（True Negative Rate，TNR），也称为specificity
TNR=TN(FP+TN)=1−FPR T N R = T N ( F P + T N ) = 1 − F P R 。

考虑ROC曲线图中的四个点和一条线。
第一个点，(0,1)，即FPR=0, TPR=1，这意味着FN（false negative）=0，并且FP（false positive）=0。这是一个完美的分类器，它将所有的样本都正确分类。
第二个点，(1,0)，即FPR=1，TPR=0，类似地分析可以发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案。
第三个点，(0,0)，即FPR=TPR=0，即FP（false positive）=TP（true positive）=0，可以发现该分类器预测所有的样本都为负样本（negative）。
第四个点（1,1），分类器实际上预测所有的样本都为正样本。经过以上的分析，我们可以断言，ROC曲线越接近左上角，该分类器的性能越好。

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。
个合适的分类器，要求做到TPR较高而FPR较小，体现在曲线上，就是在相同的FPR时，TPR越大的越好：

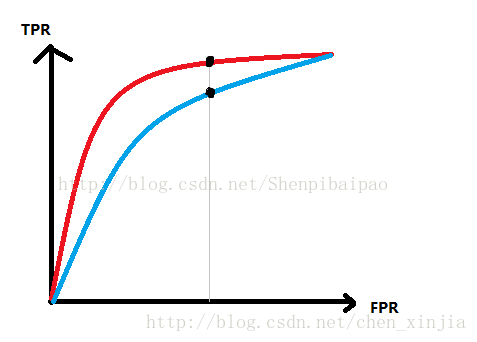
如上图中，红线对应的分类器的性能就好过蓝线对应的分类器。

但对于人类来说，通过人眼识别自然很简单。但对于计算机呢？而且，某些情况下，ROC曲线并不一定是完全光滑的（由于阈值取值的问题等），有可能某一个时刻红线超过了蓝线而另一个时刻蓝线超过了红线，这就很难进行判断到底哪个分类器性能好。

ACC被称作“准确率”，其含义为，对所有样本，被准确判断为阳性和阴性所占的比例。
ACC=(TP+TN)/所有数据的个数=(TP+TN)(TP+TN+FP+FN) A C C = ( T P + T N ) / 所 有 数 据 的 个 数 = ( T P + T N ) ( T P + T N + F P + F N )

https://blog.csdn.net/Shenpibaipao/article/details/78033218
http://alexkong.net/2013/06/introduction-to-auc-and-roc/
https://blog.csdn.net/chjjunking/article/details/5933105

判别式模型 vs. 生成式模型

判别模型与生成模型的最重要的不同是，训练时的目标不同，判别模型主要优化条件概率分布，使得x,y更加对应，在分类中就是更可分。而生成模型主要是优化训练数据的联合分布概率。而同时，生成模型可以通过贝叶斯得到判别模型，但判别模型无法得到生成模型。link
判别式模型
判别式分析 该模型主要对p(y|x)建模，通过x来预测y。在建模的过程中不需要关注联合概率分布。只关心如何优化p(y|x)使得数据可分。通常，判别式模型在分类任务中的表现要好于生成式模型。但判别模型建模过程中通常为有监督的，而且难以被扩展成无监督的。

生成式模型
该模型对观察序列的联合概率分布p(x,y)建模，在获取联合概率分布之后，可以通过贝叶斯公式得到条件概率分布。生成式模型所带的信息要比判别式模型更丰富。除此之外，生成式模型较为容易的实现增量学习。

http://www.cnblogs.com/ranjiewen/articles/6736640.html
http://www.cnblogs.com/fanyabo/p/4067295.html
http://www.cnblogs.com/kemaswill/p/3427422.html

---

决策树

信息熵 entropy

熵（entropy)表示随机变量不确定性的度量，设X是一个取有限个值的离散随机变量。基概率分布是

P(X=xi)=pi,i=1,2,⋯,n P ( X = x i ) = p i , i = 1 , 2 , ⋯ , n

则随机变量熵的定义为

H(X)=−∑i=1npilogpi H ( X ) = − ∑ i = 1 n p i log ⁡ p i

熵只与X的分布有关，而与X的取值无关。熵越大，随机变量的不确定性越大。

条件熵 conditional entropy

条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性，定义为X给定条件下Y的条件概率分布的熵对X的期望。

H(Y|X)=∑i=1npiH(Y|X=xi) H ( Y | X ) = ∑ i = 1 n p i H ( Y | X = x i )

经验熵（empirical entropy）经验条件熵（empirical conditional entropy）

概率由极大似然估计（数据估计）得到时。

信息增益

特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下的经验条件熵H(D|A)之差，即

g(D,A)=H(D)−H(D|A) g ( D , A ) = H ( D ) − H ( D | A )

决策树中的信息增益等价于训练数据集中类与特征的互信息（mutual information)。
信息增益大的特征具有更强的分类能力。
计算过程 ：
1）计算数据集D的经验熵H(D)，数据分成了k个类别。

H(D)=−∑k=1K|Ck||D|log2|Ck||D| H ( D ) = − ∑ k = 1 K | C k | | D | log 2 ⁡ | C k | | D |

2）计算特征A对数据集D的经验条件熵H(D|A),对条件A来说，A的取值有n种。Di表示A=i时的数据。

H(D|A)=∑i=1n|Ci||D|H(Di)=−∑i=1n|Ci||D|∑k=1K|Ck||D|log2|Ck||D| H ( D | A ) = ∑ i = 1 n | C i | | D | H ( D i ) = − ∑ i = 1 n | C i | | D | ∑ k = 1 K | C k | | D | log 2 ⁡ | C k | | D |

3）计算信息增益

g(D,A)=H(D)−H(D|A) g ( D , A ) = H ( D ) − H ( D | A )

信息增益比（information gain ratio)

以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。
特征A对训练集D的信息增益比g_R(D,A)定义为其信息增益比g(D,A)与训练集D关于特征A的值的熵H_A(D)之比。

gR(D,A)=g(D,A)HA(D) g R ( D , A ) = g ( D , A ) H A ( D )

其中， HA(D)=−∑ni=1|Di||D|log2|Di||Di| H A ( D ) = − ∑ i = 1 n | D i | | D | log 2 ⁡ | D i | | D i | ,n是特征A的取值个数。就是计算变量A的熵。

决策树（decision tree)

包含决策树的特征选择、决策树的生成、剪枝。
ID3选择了最大信息增益的特征进行生长。（直到所有信息增益均很小或没有特征选择为止，只有树的生成，容易过拟合。）
C4.5用信息增益比选择特征。（信息增益比阈值小于e，停止。）
剪枝通过极小化决策树整体的损失函数实现。

CART算法（classification and regression tree) 分类与回归树

选择最优特征的最优划分点，ID3和C4.5只是选择特征划分。
CART回归：平方误差最小化。
CART分类：Gini指数（选择最小的）。