随机森林实例：利用基于CART算法的随机森林（Random Forest）树分类方法对于红酒质量进行预测

1、引言

随机森林（Random Forest）是一种基于决策树的集成学习（Ensemble Learning）方法，其基本思想是通过集成学习的思想将多课决策树集成的一种算法，基本构成单元是决策树，本质上为集成学习方法。随机森林可以分为两个部分来看，一部分是“随机”，另一部分是“森林”。所谓“森林”，就是指由很多棵“树”构成的，每一棵树都是一棵决策树；而“随机”的含义则会在后续的理论介绍部分详细介绍。对于我们所要研究的分类问题而言，直观上来说，每棵决策树都是对于给定数据集的一个“分类器”，如果我们所建立的森林有N棵决策树，那么对于一个给定数据就能得到N个分类结果，随机森林再将所有的结果集合起来，投票选出次数最多的结果作为最终的输出。

作为新兴起的、高度灵活的一种机器学习算法，随机森林（Random Forest，简称RF）拥有广泛的应用前景，从市场营销到医疗保健保险，既可以用来做市场营销模拟的建模，统计客户来源，保留和流失，也可用来预测疾病的风险和病患者的易感性。

2、理论基础

2.1 什么是决策树

决策树算法（Decision Tree）算法是一种基本的分类与回归方法，是我们最经常使用的数据挖掘算法之一。决策树模型是一种树形结构，在常见的分类问题中，表现为基于特征对于数据实例进行分类的过程，其基本规则是if-then规则。如下图所示，对于一组具有二维特征变量的数据，利用两个叶节点的处理后，我们可以将数据的两种分类区分开来；从空间上来说，是将数据空间按其分类分为了两个部分。一般而言，决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪三个步骤。

2.2 特征选择的算法

决策树最重要的步骤就是如何选择合适的标准对于数据进行分类。而对于数据进行分类的依据是信息增益。

这里首先要引入信息论的相关知识：

熵（entropy）：熵指的是体系的混乱程度

信息论（information theory）中的熵（又称为香农熵）：是一种信息度量方式，表示的第一个数据集中的信息的混乱的程度，一般而言，数据集中的信息越有序，信息熵越低， 信息越无序，信息熵就越高。对于数据分类而言，一组数据中的类别越多，其信息的混乱程度也就越高，类别越少其混乱程度越低。下图表示了包含了两类数据的数据组的数据构成比例与其信息混乱程度之间的关系，可以看到当数据越接近于由单一类别构成时，信息混乱程度越低，而数据构成越接近于1:1时（对于两类数据而言），其信息混乱程度越来越高。

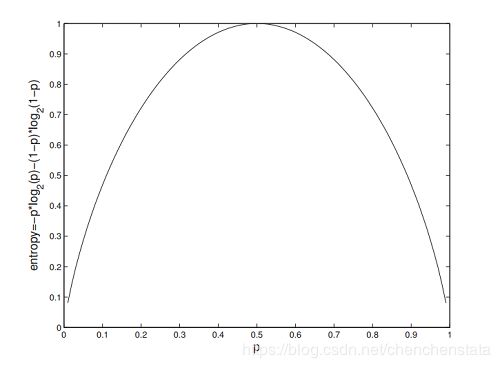
信息增益（information gain）：指的是在选定特征划分数据集前后的信息熵的变化情况。 一般来说，决策树在决定信息混乱程度的常见算法有三种，即：

2.2.1 ID3：基于信息增益的特征划分

ID3算法的信息增益算法基础是香农熵，熵定义为信息的期望值。如果待分类的对象可能被划分在多个种类中，那么我们定义对象x_i的信息为：

$$l(x_i)=-{\log }_2\left(p(x_i)\right)$$

其中$p(x_i)$是选择该分类的概率。为了对于数据集的熵进行计算，我们需要对于所有类别所有可能值包含的信息期望值，即有：

$$H(D)=-\sum _{k=1}^K\frac{|C_k|}{D}{\log }_2\frac{|C_k|}{D}=-{\sum }_{i=1}^{n}p(x_i){\log }_{2}p(x_i)$$

信息增益可以表示为：
$$g(D,A)=H(D)-H(D|A)$$$$H(D|A)=\sum _{i=1}^n\frac{D_i}{D}H(D_i)=-\sum _{i=1}^n\sum _{k=1}^K\frac{|D_{ik}|}{D_i}\log \frac{|D_{ik}|}{D_i}$$
其中$n$为分类的数目。那么在ID3基于信息增益的算法下，我们所寻找的特征划分对象便是让数据集切分后的两个新的数据集的信息熵之和最小的特征，也就是选取信息增益最大的特征作为划分对象数据集的切割点，其表示的是信息不确定性减少的程度。这个切分并非为一分为二的，而有可能是多叉的，例如按年龄范围分为（儿童，成年，老年）则会将数据分为三份。但ID3算法所采用的信息增益度量存在一个内在偏置，即它会优先选择有较多属性值的特征，因为按照属性值较多的特征对于数据进行划分会有更大的信息增益，但这样一来相当于建立了多个模型，算法复杂程度增加。

2.2.2 C4.5：基于信息增益比的特征划分

C4.5算法与ID3算法的差异性在于ID3算法将信息增益作为选择数据切分的标准，而C4.5算法则是将信息增益率（gainratio）作为数据切分的标准。通过引入一个名为分裂信息（splitinformation）的项来惩罚那些有着众多取值的特征（例如个人ID）：

$$SplitInformation(D,A)=-\sum _{i=1}^n\frac{|D_i|}{D}\log \frac{|D_i|}{D}$$$$GainRatio(D,A)=\frac{g(D,A)}{SplitInformation(D,A)}$$

相比于ID3算法，C4.5的另一个优势在于其还够处理连续属性值。

CART：基于基尼指数的特征划分

与上述两个方法不同的是CART算法，其特征划分基于的是基尼系数的增益：

$$Gini(D)=1-\sum _{i=1}^m{p}_i^2$$$$Gini(D)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$$$$△Gini(A)=Gini(D)-Gin{i}_A(D)$$

CART假设决策树是二叉树而非ID3与C4.5所用的多叉树，内部结点的特征取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征，将输入空间即特征空间划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。相比于ID3和C4.5算法，CART算法的优势在于（1）CART算法既可以用于离散型数据，也可以用于连续型数据；（2）CART算法对缺失值不敏感；（3）CART算法在处理大样本数据时处理成本耗时低，但对小样吧处理下泛化误差大；（4）CART算法不仅可以做分类，也可以做回归。

2.3 基于CART算法的决策树的构建

具体来说基于CART算法的决策树的构建方法如下：

1. 设该结点下的训练数据集为D，计算该训练数据集的所有特征对数据集的基尼指数。
2. 对于训练数据集中的每个特征的每一个可能的取值都将其作为可能的数据划分结点，对每一个选择的可能的数据划分点，将数据划分为两个部分，计算划分后的两个数据集的剩余特征作为对象的基尼系数和。
3. 在计算所有划分情况下的基尼系数后，选择能让基尼系数最小的划分特征和特征值
4. 循环进行（1）（2）（3），直至特征使用完成或满足停止条件
5. 生成CART决策树

2.4 决策树的修剪

通过CART构建的决策树在不进行剪枝的情况下，生成的决策树会考虑数据集中的每个特征，决策树的树叶节点所覆盖的训练样本都是“纯”的。因此在我们从训练样本得到的决策树对于训练样本去进行分类时，就会发现其在对于训练样本进行训练时表现良好，误差率极低。但是也存在一个问题，训练样本中的错误也会被决策树学习，成为我们构建的决策树的一部分，故而在对于测试数据进行分类时往往其分类的准确性就会下降甚至极差，这就出现了我们所谓的“过拟合”（Overfitting）问题。

对于这种问题，对于决策树进行一定的限制就是有必要的，决策树的剪枝就是有效限制树模型复杂程度的好方法。剪枝可以分为预剪枝和后剪枝两种，由于随机森林方法下无须对树模型进行剪枝操作，故而在此不多赘述。

有兴趣可参考这里

3. 随机森林

通俗来说，随机森林就是由很多棵决策树构成的“森林”，当我们要对目标类型进行预测时，每棵决策树都会给出一个结果，最终由所有决策树给出的结果进行投票得到最终的分类结果。

3.1 Bagging

随机森林是再以决策树为基学习器构建Bagging集成（样本的随机选取）的基础上，进一步在决策树的训练过程中引入随机属性选择。Bagging是集成学习的一种，其特点是多个模型之间彼此不存在依赖关系，彼此独立。利用相同的训练数据同时搭建多个独立的分类模型，然后通过投票的方式，以少数服从多数的原则做出最终的分类决策。其算法如下：

对于一个给定的含有$N$个训练样本的数据集：

1. 采用Bootstrap有放回的抽样，组成含有n个样本的新的训练集
2. 重复（1）进行$T$次得到$T$个训练集
3. 在每个训练集上采用某种分类算法独立地训练出$T$个
4. 对于每个测试数据，利用上述$T$个分类器最终会得到T个预测结果
5. 对于每个测试数据，采用多数投票的方式得到最终的预测结果

3.2 随机森林的算法

在Bagging算法的基础上给出随机森林的算法：

1. 对样本数据进行Bootstrap抽样，得到n个样本集
2. 重复（1）得到$T$个训练集
3. 对于每个训练集，从其特征变量中随机选出$m$个特征，剔除掉训练集中没有被选择的特征对应的参数，利用新的训练集构建决策树，不剪枝
4. 最终得到由$T$个决策树构成的随机森林
5. 对于每个测试数据，采用多数投票的方式得到最终的预测结果

3.3 袋外数据(out of bag)

在上面的随机森林的算法构建中，我们知道在构建每棵决策树时，需要对于特征进行随机选取，这个选取的特征个数$m$是随机森林建立过程中可以外生给定的两个数值之一，另一个数值是我们决定建立是随机森林中的决策树的棵数。减少特征的选择的个数$m$会令树的相关性降低，随之而来的是分类能力的降低，因为用于分类的信息少了；若增加我们选择的特征个数，会令相关性上升，导致潜在的过拟合的问题发生的可能性上升。故而如何选择$m$的大小成为我们构建随机森林的关键因素。

由于我们对训练数据进行Boostrap抽样时，若抽取数为$n$，那么每次抽取数据时每个数据被选取的概率为$1/n$，那么当我们的对数据进行$n$采样时，该数据没有被抽到的概率为${(1-\frac{1}{n})}^n$，当$n\to \infty$，那么我们有$\underset{n\to \infty }{\lim }{(1-\frac{1}{n})}^n\approx \frac{1}{e}$，故而有$\frac{1}{e}\approx 0.368$的数据没有被选择，这部分数据就被称为袋外数据（out of bag）。

有了袋外数据的存在，使得我们在训练决策树时无须将数据分为训练数据和测试数据，而是直接将袋外数据（out of bag）作为我们的“测试数据集”。也就是说没有必要对其进行交叉验证或者用一个独立的测试集来获得误差的一个无偏估计，它可以在其内部进行评估，也就是说在生成的过程中就可以对误差建立一个无偏估计。在构建每棵树时，我们对训练集使用看不同的bootstrap sample。所以对于每棵树而言，大约有1/3的训练实例没有参与第k棵树的生成，它们称为第k的oob样本。那么基于每棵决策树的oob样本，我们就能计算出袋外错误率（Out-of-bag error）。其算法如下：

1. 对每个数据样本，计算它作为oob样本的树对它的分类情况（这样的树大约占整个随机森林的1/3。
2. 然后利用简单多数投票作为该样本的分类结果
3. 比较投票结果和实际情况，计算错误个数占样本总数的比率作为随机森林oob的错误率。

根据Breiman(1996)给出的经验性实例表明其所得到的结果近似于需要大量计算的k折交叉验证。

3.4 注意事项

随机森林的方法是建立在两个随机采样基础上的，既对训练数据进行随机采样，又对数据特征进行采样，如此一来充分保证了我们所建立的模型的独立性，使得我们投票得到的结果更加准确。

随机森林的随机性也体现在两次采样的随机性中，从而使得我们所建立的决策树的建立也是随机的，从而即使我们没有对决策树进行剪枝，随机森林也不会产生过拟合的现象。

4 数据介绍与处理

4.1 数据预处理

本次进行随机森林分析的数据来源于阿里云天池数据库的他人分享，其原始来源应为UCI数据库中的 Wine Quality Data Set 数据集，数据描述红酒的质量与其酒精浓度、Ph值等特征，其中共有11个特征变量和1个品质特征，共12个。首先需要对于文本数据进行预处理：

#第一步导入我们所需要的库/包
from __future__ import division
import pandas as pd
import copy
import numpy as np
import random
import math
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

#第二步，将文本数据转化为list格式
data_csv = open('C:/Users/ruc_czk/Desktop/硕士课程资料/机器学习Project/winequality-red.csv','r')
data_str = []
variables = []
data = []
quality = []
for line in data_csv:
    data_str.append(line.split(';'))
for i in range(len(data_str[0])):
    variables.append(data_str[0][i].replace('"',''))
for j in range(len(data_str)-1):
    data.append(list(map(lambda x:float(x),data_str[j+1])))

由于我们对数据的基本情况未知，故而存在有重复数据的可能性，故而对数据进行一个去重的预处理：

<source lang='Python'>
def uniquedata(data):
    uniquedata = []
    for i in data:
        if i not in uniquedata:
            uniquedata.append(i)
    return uniquedata
data = uniquedata(data)

得到的结果见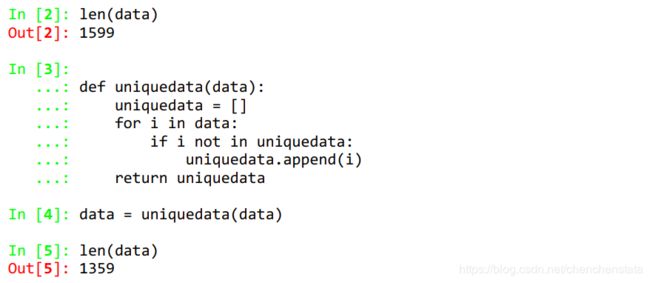从结果可知数据由原始的1599个减少到了1359个，说明存在着240个重复数据。
为了便于我们对数据进行描述性统计，暂时将数据转化为DataFrame格式：

#为了便于对于数据进行描述性统计，将数据格式转变为DataFrame格式
uniquedatamat = np.mat(data)
dataFrame = pd.DataFrame()
for i in range(len(variables)):
    featdata = []
    listtolist = uniquedatamat[:,i].tolist()
    for dt in listtolist:
        featdata.append(float(dt[0]))
    dataFrame[variables[i].strip('\n')] = featdata
dataFrame.describe()

得到输出结果如下：

可以看到数据共有特征变量11个，即fixed acidity，volatile acidity，citric acid，residual sugar，chlorides，free sulfur dioxide，total sulfur dioxide，density，Ph，sulphates，alcohol。而对于质量的分类有6个等级，形式上分别用3-8来标注。但是我们可以看到虽然等级的均值（用数值来表示）为5.623，但方差仅有0.824，再观察25%、50%、75%分位数发现：大部分的数据都集中分布在5、6两个质量等级上。对于数据进行一个更为具体的分析：

def CheckthestructureOfData(dataSet):
    classCount = {}
    classList = [dt[-1] for dt in dataSet]
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    print(classCount)

得到的结果如下：

可以发现质量等级为3、4、8的数据个数过少，数据结构中心化严重。一般而言样本类别分布不均衡是指不同类别的样本量差异巨大，可以分为大数据分布不均衡和小数据分布不均衡两种。大数据不均衡是指整体数据规模偏大，只是其中少类样本占比较少，但从每个特征的分布来看，小样本也覆盖了大部分或者全部特征，例如拥有1000万条记录的数据集中，其中占比50万条的少数分类样本便是大数据不均衡。而本次使用的对象数据是典型的小数据分布不均衡，整体规模小且占据少量样本比例的分类数量也少，从而导致很难从中提取规律。

后续学习过程中我发现上述过程其实有更加简便的实现方式，在这里给出：

df = pd.read_csv('此处为文件位置',sep=';')
df = df.drop_duplicates()#直接去掉数据库中的重复项
df['quality'].value_counts().sort_index()#观察数据结构

4.2 数据分布不均的处理方式

4.2.1 过抽样

在决策树模型中，数据类别分布差异过大会导致在最后一个叶节点对数据进行划分后，两个数据集中仍然是以多数特征的数据占主要地位（由投票选出得分最高的特征，此时少数特征就会不利），从而导致决策树在分类问题上对于多数特征的分类倾向上升的问题。对于这种样本不均衡的情况，可以采用过抽样（也称上采样，over-sampling）或欠抽样的方法对于数据进行处理。

所谓过抽样（over-sampling）方法，就是通过增加分类中少数类样本的数量来实现样本均衡，最直接的方法就是简单复制少数类样本形成多条记录，这种方法的缺点是如果样本特征少而可能导致过拟合的问题，但考虑到随机森林学习过程中的两个随机采样的过程，过拟合的问题产生的可能性较小。而欠抽样方法（under-sampling）则与过抽样方法相反，通过减少分类中多数类样本的样本数量来实现样本均衡，最直接的方法是随机地去掉一些多数类样本来减小多数类的规模，缺点是会丢失多数类样本中的一些重要信息。对于本次研究的对象数据集而言，其数据差异性过大，多数分类（quality表示为5或6的数据）在数量上大约为少数分类（quality表示为3,4,8的数据）的50倍，这使得欠抽样方法每次只会涉及到原本数据的1/50，多数类样本中的信息丢失过多，必然导致对于多数类样本的预测能力下降，故而欠抽样方法理论上不适用。尝试使用过抽样方法对于数据进行处理。

#由于数据分布不均衡，采用"过采样"方法对于数据进行处理
from imblearn.over_sampling import RandomOverSampler
oldX = df.iloc[:,:-1].values
oldy = df['quality'].values
ros = RandomOverSampler()
newX,newy = ros.fit_sample(oldX,oldy)
print(pd.DataFrame(oldy)[0].value_counts().sort_index()
#我们得到了新的数据结构更为均衡的数据

进行过抽样之后的数据结构为：

可以看到经过预处理之后的数据分布趋向平均，故而数据样本不平衡的问题得到解决。

4.2.2 SMOTE方法

SMOTE的全称为Synthetic Minority Over-Sampling Technique，即“人工少数类过采样”，其并非直接对于少数样本进行重采样，而是设计算法来人工合成一些新的少数样本。其实现方法如下图所示：

该部分的四个图片均来自：图片来源

首先，在我们的少数类样本中选择一个样本$x_i$，然后对于我们的采样倍率$N$，从$x_i$的$K$近邻中随机选择$N$个样本$x_{zi}$。最后，依次在$x_{zi}$和$x_i$之间随机合成新样本，合成公式如下：$x_n=x_i+\beta \times (x_{zi}-x_i)$。其算法原理可以表示如下：对于一组分布不均匀的二分数据进行SMOTE过采样后的结构如下：

4.3.3 Borderline SMOTE

Borderline SMOTE方法是在SMOTE方法上经过改进的方法，其基本思想是对于数据进行分类，将数据根据其近邻数据的情况分为safe，danger，noise三类。

Safe：指对于一个较大的范围的近邻区域中，若近邻区域的样本一半以上均为少数类样本，则称为Safe样本，说明该数据处在少数类样本分布区域的一个中心区域。如下图中的A样本。

Danger：指近邻样本中超过一半为多数类样本，说明该数据点已远离少数类样本分布的中心，视为少数类样本分布的边界上的样本，如图中的B点。

****：指近邻样本全部都为多数类样本点，说明该点为一个噪声点。如下图中的C。

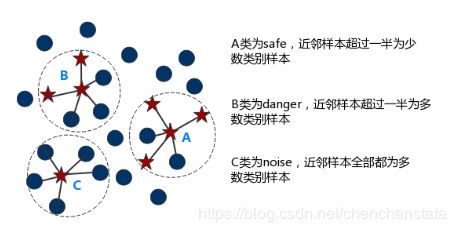
Borderline-SMOTE又可以分为两类：

1. Borderline-SMOTE1：该方法在对Danger生成新样本时，在K近邻随机选择少数类样本。

2. Borderline-SMOTE2：该方法在对Danger点生成新样本时，在K随机选择任意一个样本点，无论其是少数类样本还是多数类样本。

对于一组分布不均的二分数据进行Borderline-SMOTE1过采样后的结果如下：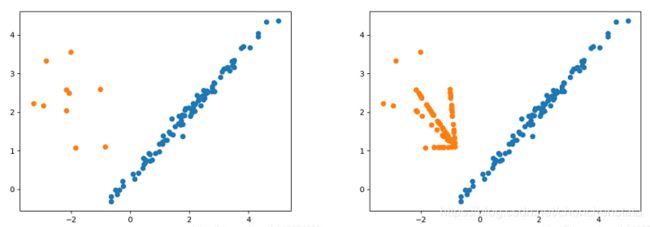

5. 随机森林建立

我们可以直接调用sklearn中的RandomForestClassifier进行决策树的建立，Code为：

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn import metrics

5.1 过抽样的合理性

首先为了验证在数据处理中对于数据进行过抽样的合理性，我们首先使用交叉验证法（Cross Validation）分别对过抽样前的原始数据（记为OriginalData）和经过过抽样后的数据（记为Data）建立一个基本的随机森林模型。

RandomForestClassifier(n_estimators,criterion,max_features,warm_start,oob_score)
n_estimators:the number of DesicionTree in the Forest
criterion:the type of algorithm,include 'gini','entropy'
max_features:The number of features to consider when looking for the best split
warm_start:When set to True, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest.
oob_score:Whether to use out-of-bag samples to estimate the generalization accuracy.
"""
df = pd.read_csv('C:/Users/ruc_czk/Desktop/硕士课程资料/机器学习Project/winequality-red.csv',sep=';')
df.drop_duplicates()#直接去掉数据库中的重复项
df['quality'].value_counts().sort_index()#观察数据结构

#由于数据分布不均衡，采用"过采样"方法对于数据进行处理
from imblearn.over_sampling import RandomOverSampler
oldX = df.iloc[:,:-1].values
oldy = df['quality'].values
ros = RandomOverSampler()
newX,newy = ros.fit_sample(oldX,oldy)

#首先考虑一下对于原始数据进行模型建立，然后对其进行评价
oldX_train,oldX_test,oldy_train,oldy_test = train_test_split(oldX,oldy,test_size = 0.2,random_state = 0)
oldclf = RandomForestClassifier(n_estimators=500)
oldclf.fit(oldX_train,oldy_train)
oldy_predit = oldclf.predict(oldX_test)
print(metrics.classification_report(oldy_test,oldy_predit))

newX_train,newX_test,newy_train,newy_test = train_test_split(newX,newy,test_size = 0.2,random_state = 0)
newclf = RandomForestClassifier(n_estimators=50)
newclf.fit(newX_train,newy_train)
newy_predict = newclf.predict(newX_test)
print(metrics.classification_report(newy_test, newy_predict))

从Code可知，我们建立了一个包含50棵决策树、以Gini算法作为数据集划分标准的决策树，且在每棵决策树建立的过程中没有对其随机选择的特征量（即$m$）作出限制，通过这种简单的随机森林的建立得到如下对于原始数据和过抽样数据的预测结果：

可以看到，在未对数据进行任何处理时，所构建的随机森林分类器对于少类样本基本没有预测能力，且出现了样本数量越多其预测准确率越高的倾向，说明样本分布的不均衡对于该分类器产生了巨大的影响。而观察经过简单过抽样后的分类器准确率预测可以发现，其对于少类样本的预测的准确率大幅上升，但准确率过高，其中对于样本分类为3、4、8的预测准确率都在98%以上，甚至对于样本分为为8的测试数据出现了100%的预测准确率，过拟合问题较为严重。

5.2 模型的拟合

首先我们想要观察一下，哪些变量对于预测结果起主要作用，哪些变量对分类结果影响并不明显。

importances = newclf.feature_importances_
std = np.std([tree.feature_importances_ for tree in newclf.estimators_],axis=0)
indices = np.argsort(importances)[::-1]

plt.figure()
plt.title("Importances of feature")
plt.bar(range(newX.shape[1]),importances[indices],color='b',yerr=std[indices],align='center')
plt.xticks(fontsize=14)
plt.xticks(range(newX.shape[1]),df.columns.values[:-1][indices],rotation=90)
plt.xlim([-1,newX.shape[1]])
plt.tight_layout()
plt.show()

得到结果如下：

可以看到对于一瓶红酒分类的影响因素中acohol、volatile acidity与sulphates的影响因素最大，且差距不明显，但与其他8个特征的差距较大，可以将其分为两个不同的层次来看待。

将原始数据经过过抽样、SMOTE过抽样与Borderline SMOTE处理后备用：

from imblearn.over_sampling import RandomOverSampler
oldX = df.iloc[:,:-1].values
oldy = df['quality'].values
ros = RandomOverSampler()
newX,newy = ros.fit_sample(oldX,oldy)

from imblearn.over_sampling import SMOTE
X_resampled_smote,y_resampled_smote = SMOTE().fit_sample(oldX, oldy)

from imblearn.over_sampling import BorderlineSMOTE
X_border_smote,y_border_smote = BorderlineSMOTE(kind='borderline-1').fit_resample(oldX, oldy)

观察三种过抽样方法所得到的结果，三种过抽样方法都将各种样本数量扩充到了681个，差别在于利用过抽样方法得到的数据是原始数据的重复，而SMOTE方法和Borderline-SMOTE方法是利用原始数据来生成新的少数类样本数据来扩充，其中Borderline-SMOTE方法在数据生成时更加严谨，只选取边界上的点来生成新的数据点。

5.3 过抽样数据的模型调参与评价

为了获得对于过抽样数据的最优的随机森林分类器，我们可以对于模型建立中的一系列参数进行调整来获得一个最优的模型。

from sklearn.model_selection import RandomizedSearchCV
blankrf = RandomForestClassifier()
n_estimators = [int(x) for x in np.linspace(start = 100,stop = 1000,num=200)]
max_features = [x+1 for x in range(11)]
max_depth = [int(x) for x in np.linspace(start = 1,stop=11,num=11)]
min_samples_split  = [int(x) for x in np.linspace(start=2,stop = 50,num = 10)]
param_list = {'n_estimators':n_estimators,'max_features':max_features,'max_depth':max_depth,'min_samples_split':min_samples_split}
RS = RandomizedSearchCV(blankrf,param_list,n_iter = 100, cv =3 ,verbose = 1 ,n_jobs = -1,random_state = 0)
RS.fit(newX_train,newy_train)
RS.best_params_

RS_df = pd.DataFrame(RS.cv_results_).sort_values('rank_test_score').reset_index(drop=True)
RS_df = RS_df.drop(['mean_fit_time', 'std_fit_time', 'mean_score_time','std_score_time', 'params', 'split0_test_score', 'split1_test_score', 'split2_test_score', 'std_test_score'],axis=1)

可以看到我们对于模型的各种参数都设定了一定的选择范围，其中随机森林的“树”目设定为100至1000，每次决策的构建所随机选取的特征数量的范围为1至11，最大树深的变化范围也为1至11，对于数据集继续进行划分的数量下限从2至50进行变化。运行后可以得到如下得分前10的组合模型：

可以直观地发现当决策树的棵数为448棵，最小划分的数据数量下限为2，随机选择的特征为3，树深为11时可以获得最高的得分情况。但是在上述调参过程中，我们是对于各类参数进行的一个随机组合，故而反映出来的结构具有较大的随机性，因为范围较小。为了获得每个参数的平均的得分，我们作出每个超参数的得分柱状图。

import seaborn as sns
fig,axs = plt.subplots(ncols=2,nrows=2)
sns.set(style='whitegrid',color_codes=True,font_scale=2)
fig.set_size_inches(30,25)
sns.barplot(x='param_n_estimators',y='mean_test_score',data=RS_df,ax=axs[0,0],color='lightgrey')
axs[0,0].set_ylim([.50,.75])
axs[0,0].set_title(label='n_estimators',size=30,weight='bold')
sns.barplot(x='param_min_samples_split', y='mean_test_score', data=RS_df, ax=axs[0,1], color='coral')
axs[0,1].set_ylim([.50,.75])
axs[0,1].set_title(label = 'min_samples_split', size=30, weight='bold')
sns.barplot(x='param_max_features', y='mean_test_score', data=RS_df, ax=axs[1,0], color='wheat')
axs[1,0].set_ylim([.70,.705])
axs[1,0].set_title(label = 'max_features', size=30, weight='bold')
sns.barplot(x='param_max_depth', y='mean_test_score', data=RS_df, ax=axs[1,1], color='lightpink')
axs[1,1].set_ylim([0,.86])
axs[1,1].set_title(label = 'max_depth', size=30, weight='bold')

得到如下的结果：

可以看到组成森林的决策树的棵数其实对于模型的得分结果的影响并不显著，从100到1000棵的平均得分内基本上都在70%附近波动，一般而言决策树的棵数越多模型越精确，可以看到虽然600-1000的区间内平均得分差别不明显，但在极值上900最高，故而左上图说明取900棵左右的数目的决策树就足够了，更多了决策树数量并不会大幅度提高我们预测的准确率。最小数据划分数量其准确率与其取值的关系相对于决策树数量更为明显，可以看到当这个值大于12时，其预测准确率相对于小于12的取值有一个显著的下降，故而min_sample_split的潜在取值可为2、7、12。Max_features这一项的取值可以看到取值为2时有最高的得分极值和平均值且与其他取值之间的差别明显。Max_depth这一项对于准确率的影响表现出了明显的正向影响，我们所构建的决策树越大其模型越复杂，过拟合现象发生的可能性越大，可以看到当取值大于8后，其准确率基本没有较大提升，故而这一项可能的取值为7至10。

接下来为了获得最适合的对于过抽样数据的模型，我们选择n_estimators为900，min_sample_split为2、7、12，max_features为2，以及max_depth为8、9、10进行组合后选择最合适的模型，利用混淆矩阵对于模型进行评价。

from sklearn.metrics import confusion_matrix
label = ['3','4','5','6','7','8']
tick_marks = np.array(range(len(label)))+0.5

def plot_confusion_matrix(cm,title='Confusion Matrix',cmap=plt.cm.binary):
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    xlocations = np.array(range(len(label)))
    plt.xticks(xlocations, label, rotation=90)
    plt.yticks(xlocations, label)
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

plt.figure(figsize=(12, 8), dpi=120)
ind_array = np.arange(len(label))
x, y = np.meshgrid(ind_array, ind_array)

for x_val, y_val in zip(x.flatten(), y.flatten()):
    c = cm_normalized[y_val][x_val]
    if c > 0.01:
        plt.text(x_val, y_val, "%0.2f" % (c,), color='blue', fontsize=15, va='center', ha='center')
# offset the tick
plt.gca().set_xticks(tick_marks, minor=True)
plt.gca().set_yticks(tick_marks, minor=True)
plt.gca().xaxis.set_ticks_position('none')
plt.gca().yaxis.set_ticks_position('none')
plt.grid(True, which='minor', linestyle='-')
plt.gcf().subplots_adjust(bottom=0.15)

plot_confusion_matrix(cm_normalized, title='Normalized confusion matrix')
# show confusion matrix
plt.show()

下面三个混淆矩阵图从左至右分别表示n_estimators为900，min_sample_split为2，max_features为2的情况下，将max_depth从8变化到11的模型对于测试数据的预测准确率情况。可以发现三个模型对于少数样的预测情况都非常好，原因在于对于少数类样本进行过抽样后（从过抽样前的数据数量和过抽样后的数据数量大小的对比），就可以看出其实过拟合现象还是十分严重，而对于多数类样本的分类情况可以看到随着max_depth的上升，模型复杂程度的增加，其预测准确率是逐渐上升的，无论是对于标签为5还是标签为6的数据。

通常而言，max_depth取值越大，说明每一个决策树也就越大，树越复杂，从而过拟合的风险也会上升。由于max_depth从9上升到10后对于标签6的数据的准确率上升了9%，而从10上升到11仅上升了3%，对于过拟合与模型的预测准确率之间的权衡下，我们认为10是一个更好的参数选择。接下来再对于min_sample_split这个指标进行调整分别取7或者12作其混淆矩阵图：

可以看到，当我们将min_sample_split由2调整为7或者12后，受影响最大的是标签6，其预测准确率下降至低于70%，且预测结果向正确结果两侧发散的情况恶化，错误预测为5和7的概率都有所上升，同样的预测结果发散的情况还出现在标签5和标签7上，故而为了将标签6的预测准确率控制在70%以上，min_sample_split选取2。

可以发现在普通过抽样下，对于少数类样本的过拟合无法控制，特别是在数量差距过大的情况下，而且该模型对于标签6的样本的预测能力很差，可能的原因在于对于max_features这一参数固定为2使得原始数据丢失了过多的信息，我们尝试着将max_features从2至11变化，以标签5和标签6的预测准确率为标准来选择最优的模型。

各个模型的混淆矩阵结果见:

可以看到其实对于标签5和标签6的数据的预测准确率并没有很大的影响，但是值得注意的是预测结果的分布情况，当max_features大于等于7后，对于标签6的数据的预测的分布更加分散了，这是我们不能接受的，故而选择max_features为5。

由于怀疑多类样本数据存在着较多的噪声，且将原始数据分为训练集和测试集后，无论是训练集还是测试集都可能存在噪声，故而选用LOF方法对于标签为5的数据进行10%、标签为6的数据进行20%的降噪处理后再拟合，观察利用LOF方法降噪处理后的数据建立的分类器的效果。

dataclean6 = LocalOutlierFactor(n_neighbors = 70, contamination = 0.1)
predictlabel = dataclean6.fit_predict(label6_data)
label6_data_normal = np.array(label6_data)[predictlabel>0]

对于降噪后的数据建立一个n_estimators = 900,min_samples_split=2,max_depth=10,max_features=5的模型，得到的混淆矩阵如下：

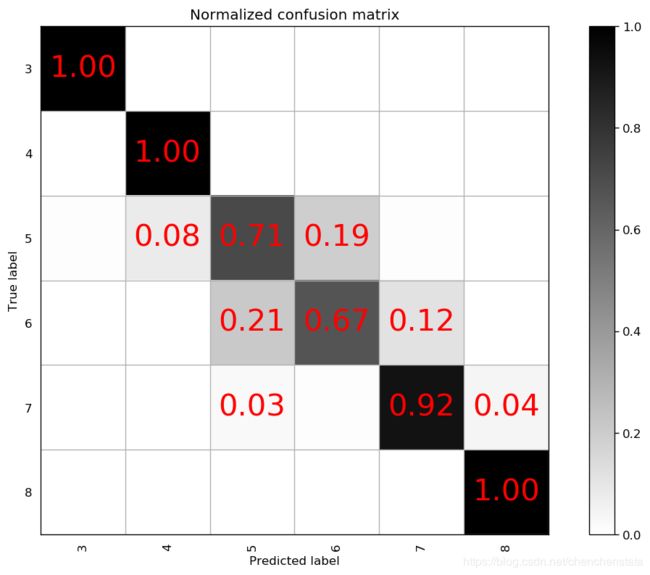可以看到，进行降噪处理后，对于标签6这个种类的预测度下降至0.61，且对于标签5的预测准确率下降至0.70，且将标签5的数据预测为标签6的概率上升至19%，说明对于标签6的数据进行降噪处理之后会使标签5和标签6的数据更相似了。若将max_feature重新调整为2，其预测准确率相较于左图有所上升，但仍然远低于降噪之前的水准。故而最优的过抽样分类器为n_estimators=900,max_features=5,min_sample_split=2,max_depth=10的随机森林模型，其对应的混淆矩阵如下：

虽然该分类器对于多数样本标签5与标签6的预测准确率不是非常高（前者为88%，后者为75%），但是这个模型将标签5和标签6的数据分为其他的类型的概率是很低的，对于标签5的数据其分类为5或6的概率为0.95；而对于标签6的数据预测为标签5或标签6的概率为0.86。若在实际情况中对于这两类红酒的质量的区别不大的话，该分类器还是具有较好的分类能力，但仍存在着对于少数样本国拟合的问题。

5.4 SMOTE方法与Borderline SMOTE方法模型的调参与评价

为了降低分类器过拟合的问题，尝试使用SOMTE方法与Borderline-SMOTE方法对于数据进行处理。

可以看到相比于简单过抽样，由于SMOTE加入了更多的噪声数据，使得整体的预测得分都有所下降。由调参结果可知，参数选择基本上与简单过抽样得到的结果一致。选用不同的参数作混淆矩阵得到如下结果：

可以看到参数为n_estimators=900,min_samples_split=2,max_depth=10,max_features=2的参数下所建立的模型，从少数样本来看，其预测准确率仍然是100%，但对于多数类样本的预测准确率大大下降了，而且相较于之前的模型多数类样本的预测分布也更加发散了，相较于之前的模型过拟合问题的解决与多数类样本预测准确率的权衡下，我们还是倾向于之前的模型。接下来再用Borderline-SMOTE方法对数据进行处理：
相比于单纯的SMOTE方法，可以看到Borderline-SMOTE方法确实在噪声数据的生成上更加合理，模型的预测的准确率有所上升，且相对而言对于少数类样本的过拟合现象是有所缓解的，但是对于多数类样本的预测准确率仍然太低，特别是对于标签6的样本，该分类器有28%的概率将其预测为标签7。可见由于本次使用数据的设置，为了控制多数类样本的预测的准确率，我们不得不放松对于过拟合的控制，故而对于数据的SMOTE处理，由于进一步加大了对于多数类样本的噪声，使得模型对于标签5和标签6的数据的预测准确率进一步下降了，故而不适用。

5.5 与其他方法的比较

为了验证模型的好坏，我们尝试用一些常见的分类模型对于数据进行拟合，比较其与我们建立的随机森林模型之间的差异。

如上图给出的分别是AdaBoost、Decision Tree、LDA、Linear SVM、Naive Bayes、Nearest Neighbors、QDA以及RBF SVM方法给出的分类器对应的混淆矩阵。可以很明显的看到，AdaBoost方法对于测试数据的拟合效果最差，Decision Tree方法与LDA、Liner SVM、Naive Bayes的分类效果相差无几，但这些方法与随机森林方法相比的预测结果差距很大。表现相对来说较好的为Nearest Neighbors与RBF SVM方法，但相比于随机森林方法，Nearest Neighbors的问题在于对于样本数量前三的样本分类的预测准确率均低于随机森林方法，而RBF SVM方法在除标签5以外的数据都拟合效果较好，唯一的缺点在于无论我们如何对于RBF SVM方法进行调参都无法调高对于标签5数据的预测准确率甚至不能将其提高至60%以上，结合我们之前在random forest方法中遇到了将标签5预测为标签6的这种倾向，数据中标签5和标签6的分类本身即数据本身的问题可能是造成分类器对于标签5的错判的原因。

5.6 总结

可以看到由于该数据自身的特性，无论用哪种方法对于数据进行建模，都难以避免对于标签5和标签6数据的类似性的处理。以CART算法建立的Random Forest分类器相比于其他分类器方法有着更好的对于多数类样本预测的准确率。但是仍在存在着以下两个问题：（1）对于少数类样本的预测，由于在进行模型建立前我们对数据进行了过抽样的处理，这使得对于少数类样本的过拟合不可避免。我们曾经尝试用SMOTE方法和Borderline-SMOTE方法对于数据进行过抽样处理，但结果并不明显，也就是说该分类器存在一定的过拟合的问题。（2）虽然相比于其他方法，Random Forest方法对于多数类样本的预测准确率较好（对于标签5为88%，对于标签6为75%），但仍然不高，可能进一步的对于数据的处理和其他可能的方法的组合（例如SVM方法等）对于该数据有着更好的预测准确率。

6 部分参考文献

[1] Nitesh V. Chawla, Kevin W. Bowyer, Lawrence O. Hall,等. SMOTE: Synthetic Minority Over-sampling Technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1):321-357.
[2] Han H , Wang W Y , Mao B H . Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning[J]. 2005.
[3] SHI Hongbo,CHEN Yuwen,CHEN Xin.Summary of research on SMOTE oversampling and its improved algorithms[J].CAAI Transactions on Intelligent Systems,2019,14(06):1073-1083.
[4] Breiman L . Bagging predictors" Machine Learning[J]. Machine Learning, 1996, 24.

7 参考BLOG

1. 数据挖掘领域十大经典算法之—CART算法
2. 机器学习 随机森林（Random Forest）
3. 随机森林算法总结
4. 随机森林之oob error 估计
5. sklearn随机森林分类类RandomForestClassifier
6. 项目实例—随机森林在Kaggle实例:Titanic中的应用(一)
7. 如何用python画好confusion matrix
8. 机器学习-Confusion Matrix混淆矩阵、ROC、AUC
9. Python中生成并绘制混淆矩阵（confusion matrix）
10. 不平衡数据处理之SMOTE、Borderline SMOTE和ADASYN详解及Python使用
11. SMOTE过采样处理不均衡数据（imbalanced data）