算法——字符串匹配之BM算法
前言
Boyer-Moore算法是一种基于后缀匹配的模式串匹配算法(简称BM算法),后缀匹配就是模式串从右到左开始比较,但模式串的移动依然是从左到右的。在实践中,BM算法效率高于前面介绍的《KMP算法》,算法分为两个阶段:预处理阶段和搜索阶段;预处理阶段时间和空间复杂度都是是O(m+sigma),sigma是字符集大小,一般为256;在最坏的情况下算法时间复杂度是O(m*n);在最好的情况下达到O(n/m)。
BM算法实现
BM算法预处理过程
BM算法有两个规则分别为坏字符规则(Bad Character Heuristic)和好后缀规则(Good Suffix Heuristic);这两种规则目的就是让模式串每次向右移动尽可能大的距离。BM算法是每次向右移动模式串的距离是,按照好后缀算法和坏字符算法计算得到的最大值。以下给出基本概念:
坏字符:输入文本字符串中的字符与模式串当前字符不匹配时,则文本字符串的该字符称为坏字符;
好后缀:是指在遇到坏字符之前,文本串和模式串已匹配成功的字符子串;
下面是坏字符和好后缀的图示:
坏字符规则:当输入文本字符串中的某个字符跟模式串的某个字符不匹配时,模式串需要向右移动以便进行下一次匹配,移动的位数 = 坏字符在模式串中对应的位置 - 坏字符在模式串中最右出现的位置。此外,如果模式串中不存在"坏字符",则最右出现位置为-1;所以坏字符规则必然有两种情况,下面会进行讨论。
好后缀规则:当字符失配时,后移位数 = 好后缀在模式串中对应的位置 - 好后缀在模式串上一次出现的位置,且如果好后缀在模式串中没有再次出现,则为-1。根据模式串是否存在好后缀或部分好后缀,可以分为三种情况,下面会逐一讨论。
坏字符规则
坏字符规则有两种情况,如下图所示:
好后缀规则
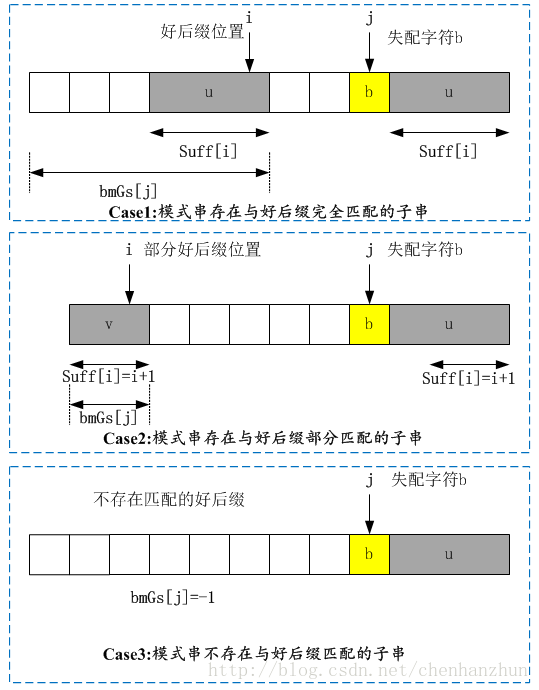
若文本字符串和模式串匹配了一个好后缀u, 下面根据模式串其他位置是否存在好后缀进行不同的移动;假如,模式串pat的后u个字符和文本串txt都已经匹配了,但是下一个字符是坏字符,则需要移动模式串重新匹配。若在模式中依然存在相同的后缀或部分后缀, 那把最长的后缀或部分后缀移动到当前后缀位置;若模式串pat不存在其他的好后缀,则直接右移整个pat。因此好后缀规则有三种情况,如下图所示:
好后缀规则和坏字符规则的大小通过模式串的预处理数组的简单计算得到。坏字符算法的预处理数组是bmBc[],好后缀算法的预处理数组是bmGs[]。
计算坏字符数组bmBc[]
Case1:若模式串存在坏字符,若模式串存在多个坏字符时,选取最右边的那个字符。bmBc['b']表示字符b在模式串中最右出现的位置。
例如下面模式串中出现坏字符b的位置分别为j,k,i;则选取最右位置i作为bmBc['b']的值;
Case2:字符在模式串中没有出现,如模式串中没有字符b,则bmBc['b'] = -1。坏字符数组bmBc[]源码实现如下:
void PreBmBc(const string &pat, int m, int bmBc[])
{
int i = 0;
// Initialize all occurrences as -1, include case2
for(i = 0; i < MAX_CHAR; i++)
bmBc[i] = -1;
// case1:Fill the actual value of last occurrence of a character
for(i = 0; i < m; i++)
bmBc[pat[i]] = i;
}计算好后缀数组bmGs[]
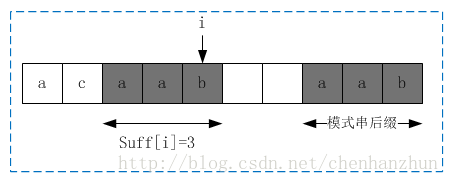
求解好后缀数组之前先求解好后缀数组长度的辅助数组suff[];![]() 表示以i为边界,与模式串后缀匹配的最大长度,如下图所示:
表示以i为边界,与模式串后缀匹配的最大长度,如下图所示:
suff[i]就是求pat中以i位置字符为后缀和以最后一个字符为后缀的公共后缀串的长度(包括当前位置字符);下面举例说明:
i : 0 1 2 3 4 5 6 7
| | | | | | | |
pat: b c a b a b a b
/*
当i=m-1=7时,则suff[7]=8;
当i=6时,以pat[6]为后缀的后缀字符串为bcababa,以最后一字符b为后缀的后缀字符串为bcababab
则不存在公共最长子串,即suff[6]=0;
当i=5时,以pat[5]为后缀的后缀字符串为bcabab,以最后一字符b为后缀的后缀字符串为bcababab
则公共最长子串abab,即suff[5]=4;
当i=4时,以pat[4]为后缀的后缀字符串为bcaba,以最后一字符b为后缀的后缀字符串为bcababab
则不存在公共最长子串,即suff[4]=0;
.......
当i=0时,以pat[0]为后缀的后缀字符串为b,以最后一字符b为后缀的后缀字符串为bcababab
则公共最长子串b,即suff[0]=1;
*/suff数组的定义:引用自《Boyer-Moore algorithm》
对于![]() ;
;![]()
其中m为模式串的长度,![]() ;所以很容易源码实现如下:
;所以很容易源码实现如下:
void suffix(const string &pat, int m, int suff[])
{
int i, j;
suff[m - 1] = m;
for(i = m - 2; i >= 0; i--)
{
j = i;
while(j >= 0 && pat[j] == pat[m - 1 - i + j]) j--;
suff[i] = i - j;
}
}则可以写出好后缀数组bmGs[]的源代码:
void PreBmGs(const string &pat, int m, int bmGs[])
{
int i, j;
int suff[SIZE];
// computed the suff[]
suffix(pat, m, suff);
// Initialize all occurrences as -1, include case3
for(j = 0; j < m; j++)
{
bmGs[j] = -1;
}
// Case2
j = 0;
for(i = m - 1; i >= 0; i--)
{
if(suff[i] == i + 1)
{
for(; j < m - 1 - i; j++)
{
if(bmGs[j] == -1)
bmGs[j] = i;
}
}
}
// Case1
for(i = 0; i <= m - 2; i++)
{
j = m - 1 - suff[i];
bmGs[j] = i;
}
}BM算法匹配过程
到此为止已经讲解了BM算法的求解方法,以下给出BM算法的程序:
#include
#include
using namespace std;
const int MAX_CHAR = 256;
const int SIZE = 256;
static inline int MAX(int x, int y){return x < y ? y:x;}
void BoyerMoore(const string &pat, const string &txt);
int main()
{
string txt = "abababaacbabaa";
string pat = "babaa";
BoyerMoore(pat,txt);
system("pause");
return 0;
}
void PreBmBc(const string &pat, int m, int bmBc[])
{
int i = 0;
// Initialize all occurrences as -1, include case2
for(i = 0; i < MAX_CHAR; i++)
bmBc[i] = -1;
// case1:Fill the actual value of last occurrence of a character
for(i = 0; i < m; i++)
bmBc[pat[i]] = i;
}
void suffix(const string &pat, int m, int suff[])
{
int i, j;
suff[m - 1] = m;
for(i = m - 2; i >= 0; i--)
{
j = i;
while(j >= 0 && pat[j] == pat[m - 1 - i + j])
j--;
suff[i] = i - j;
}
}
void PreBmGs(const string &pat, int m, int bmGs[])
{
int i, j;
int suff[SIZE];
// computed the suff[]
suffix(pat, m, suff);
// Initialize all occurrences as -1, include case3
for(j = 0; j < m; j++)
bmGs[j] = -1;
// Case2
j = 0;
for(i = m - 1; i >= 0; i--)
{
if(suff[i] == i + 1)
{
for(; j < m - 1 - i; j++)
{
if(bmGs[j] == -1)
bmGs[j] = i;
}
}
}
// Case1
for(i = 0; i <= m - 2; i++)
{
j = m - 1 - suff[i];
bmGs[j] = i;
}
}
void BoyerMoore(const string &pat, const string &txt)
{
int j, bmBc[MAX_CHAR], bmGs[SIZE];
int m = pat.length();
int n = txt.length();
// Preprocessing
PreBmBc(pat, m, bmBc);
PreBmGs(pat, m, bmGs);
// Searching
int s = 0;// s is shift of the pattern with respect to text
while(s <= n - m)
{
j = m - 1;
/* Keep reducing index j of pattern while characters of
pattern and text are matching at this shift s */
while(j >= 0 && pat[j] == txt[j + s])
j--;
/* If the pattern is present at current shift, then index j
will become -1 after the above loop */
if(j < 0)
{
cout<<"pattern occurs at shift :"<< s< http://www-igm.univ-mlv.fr/~lecroq/string/node14.html
http://blog.csdn.net/v_july_v/article/details/7041827
http://blog.jobbole.com/52830/
http://www.searchtb.com/
http://www.geeksforgeeks.org/pattern-searching-set-7-boyer-moore-algorithm-bad-character-heuristic/
http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
http://dsqiu.iteye.com/blog/1700312