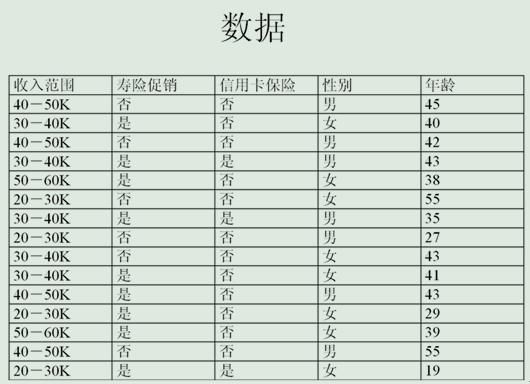
数据挖掘实验报告-决策树程序实验

【摘要】

众所周知，数据库技术从20世纪80年代开始，已经得到广泛的普及和应用。随着数据库容量的膨胀，特别是数据仓库以及web等新型数据源的日益普及，人们面临的主要问题不再是缺乏足够的信息可以使用，而是面对浩瀚的数据海洋如何有效地利用这些数据。

从数据中生成分类器的一个特别有效的方法是生成一个决策树（Decision Tree）。决策树表示方法是应用最广泛的逻辑方法之一，它从一组无次序、无规则的事例中推理出决策树表示形式的分类规则。决策树分类方法采用自顶向下的递归方式，在决策树的内部结点进行属性值的比较并根据不同的属性值判断从该结点向下的分支，在决策树的叶结点得到结论。所以从决策树的根到叶结点的一条路径就对应着一条合取规则，整棵决策树就对应着一组析取表达式规则。

决策树是应用非常广泛的分类方法，目前有多种决策树方法，如ID3、CN2、SLIQ、SPRINT等。

关键词：数据挖掘 知识发现   决策树（Decision Tree） ID3算法

一、问题重述

1.1相关信息

决策树是一个类似于流程图的树结构，其中每个内部结点表示在一个属性上的测试，每个分支代表一个测试输入，而每个树叶结点代表类或类分布。数的最顶层结点是根结点。一棵典型的决策树如图1所示。它表示概念buys_computer，它预测顾客是否可能购买计算机。内部结点用矩形表示，而树叶结点用椭圆表示。为了对未知的样本分类，样本的属性值在决策树上测试。决策树从根到叶结点的一条路径就对应着一条合取规则，因此决策树容易转化成分类规则。[2]

图1

ID3算法：

■     决策树中每一个非叶结点对应着一个非类别属性，树枝代表这个属性的值。一个叶结点代表从树根到叶结点之间的路径对应的记录所属的类别属性值。

■     每一个非叶结点都将与属性中具有最大信息量的非类别属性相关联。

■     采用信息增益来选择能够最好地将样本分类的属性。

信息增益基于信息论中熵的概念。ID3总是选择具有最高信息增益（或最大熵压缩）的属性作为当前结点的测试属性。该属性使得对结果划分中的样本分类所需的信息量最小，并反映划分的最小随机性或“不纯性”。

1.2问题重述

1、算法参见第八章分类与预测

2、目标概念为“寿险促销”

3、计算每个属性的信息增益

4、确定根节点的测试属性

模型求解

构造决策树的方法是采用自上而下的递归构造，其思路是：

■     以代表训练样本的单个结点开始建树（步骤1）。

■     如果样本都在同一类，则该结点成为树叶，并用该类标记（步骤2和3）。

■     否则，算法使用称为信息增益的机遇熵的度量为启发信息，选择能最好地将样本分类的属性（步骤6）。该属性成为该结点的“测试”或“判定”属性（步骤7）。值得注意的是，在这类算法中，所有的属性都是分类的，即取离散值的。连续值的属性必须离散化。

■     对测试属性的每个已知的值，创建一个分支，并据此划分样本（步骤8~10）。

■     算法使用同样的过程，递归地形成每个划分上的样本决策树。一旦一个属性出现在一个结点上，就不必考虑该结点的任何后代（步骤13）。

■     递归划分步骤，当下列条件之一成立时停止：

（a）给定结点的所有样本属于同一类（步骤2和3）。

（b）没有剩余属性可以用来进一步划分样本（步骤4）。在此情况下，采用多数表决（步骤5）。这涉及将给定的结点转换成树叶，并用samples中的多数所在类别标记它。换一种方式，可以存放结点样本的类分布。

（c）分支test_attribute=a_i没有样本。在这种情况下，以samples中的多数类创建一个树叶（步骤12）。[2]

算法 Decision_Tree(samples,attribute_list)

输入 由离散值属性描述的训练样本集samples;

候选属性集合attribute_list。

输出 一棵决策树。

（1） 创建节点N；

（2） If samples 都在同一类C中then

（3）       返回N作为叶节点，以类C标记；

（4） If attribute_list为空then

（5）       返回N作为叶节点，以samples 中最普遍的类标记；//多数表决

（6） 选择attribute_list 中具有最高信息增益的属性test_attribute;

（7） 以test_attribute 标记节点N；

（8） For each test_attribute 的已知值v   //划分 samples

（9）      由节点N分出一个对应test_attribute=v的分支；

（10）      令S_v为 samples中 test_attribute=v 的样本集合；//一个划分块

（11）      If S_v为空 then

（12）      加上一个叶节点，以samples中最普遍的类标记；

（13）      Else 加入一个由Decision_Tree(Sv,attribute_list-test_attribute)返回节点值。[1]

 

E(S)=(-9/15)log2(9/15)-(6/15)log2(6/15)=0.971

Values(收入范围)={20-30K,30-40k,40-50K,50-60K}

E(S(20-30K))= (-2/4)log2(2/4)- (2/4)log2(2/4)=1

E(S(30-40K))= (-4/5)log2(4/5)- (1/5)log2(1/5)=0.7219

E(S(40-50K))= (-1/4)log2(1/4)- (3/4)log2(3/4)=0.8113

E(S(50-60K))= (-2/2)log2 (2/2)- (0/2)log2(0/2)=0

所以

E(S,收入范围)=(4/15) E(S(20-30K)) +(5/15) E(S(30-40K)) +(4/15) E(S(40-50K)) +(2/15) E(S(50-60K))=0.7236

Gain(S,收入范围)=0.971-0.7236=0.2474

同理：计算“保险”，“性别”，“年龄”的信息增益为：

E(S)=(-9/15)log2(9/15)-(6/15)log2(6/15)=0.971

Insurance(保险)={yes, no}

E(S(yes))= (-3/3)log2 (3/3)- (0/3)log2(0/3)=0

E(S(no))= (-6/12)log2 (6/12)- (6/12)log2(6/12)=1

E(S, 保险)=(3/15) E(S(yes)) +(12/15) E(S(no)) =0.8

Gain(S, 保险)=0.971-0.8=0.171

E(S)=(-9/15)log2(9/15)-(6/15)log2(6/15)=0.971

sex(性别)={male, female}

E(S(male))= (-3/7)log2 (3/7)- (4/7)log2(4/7)=0.9852

E(S(female))= (-6/8)log2 (6/8)- (2/8)log2(2/8)=0.8113

E(S, 性别)=(7/15) E(S(male)) +(8/15) E(S(female)) =0.8925

Gain(S, 性别)=0.971-0.8925=0.0785

E(S)=(-9/15)log2(9/15)-(6/15)log2(6/15)=0.971

age(年龄)={15~40,41 ~60}

E(S(15~40))= (-6/7)log2 (6/7)- (1/7)log2(1/7)=0.5917

E(S(41 ~60))= (-3/8)log2 (3/8)- (5/8)log2(5/8)=0.9544

E(S, 年龄)=(7/15) E(S(15~40)) +(8/15) E(S(41 ~60)) =0.7851

Gain(S, 年龄)=0.971-0.7851=0.1859

三、模型评价

基于决策树的分类算法的一个最大的优点就是她在学习过程中不需要使用者了解很多背景知识（这同时也是它的最大的缺点），只要训练例子能够用属性-结论式表示出来，就能使用该算法来学习。

在ID3算法的假设空间包含所有的决策树，它是关于现有属性的有限离散值函数的一个完整空间。因为每个有限离散值函数可被表示为某个决策树，所以ID3算法避免了搜索不完整假设空间的一个主要风险：假设空间可能不包含目标函数。

ID3算法只能处理离散值的属性。首先，学习到的决策树要预测的目标属性必须是离散的，其次树的决策结点的属性也必须是离散的。[2]

四、参考文献

[1] 李雄飞 李军，《数据挖掘与知识发现》，北京：高等教育出版社，2003。

[2] 毛国君 段立娟 王实 石云，《数据挖掘原理与算法》，北京：清华大学出版社，2005。