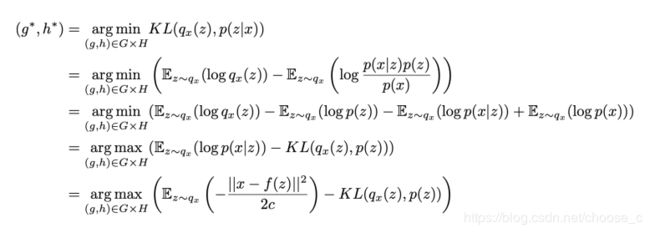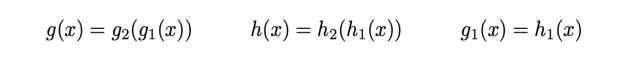深入理解VAE(变分自编码器)

原文地址：https://pan.baidu.com/s/1LNolV-_SZcEhV0vz2RkDRQ ；

本文进行翻译和总结。

VAE

VAE是两种主要神经网络生成模型中的一种，另一种典型的方法是GAN。VAE是一种自编码器，在训练时将数据编码成正则化的隐层分布，该隐层分布可以生成新的数据。其中,"变分"一词来自正则化和统计学中变分推断的关系。

本文想要解决的问题：

1.什么是自编码器？

2.什么是隐层空间，为什么需要正则化？

3.怎样使用VAE生成新的数据？

4.VAE和变分推断之间的关系?

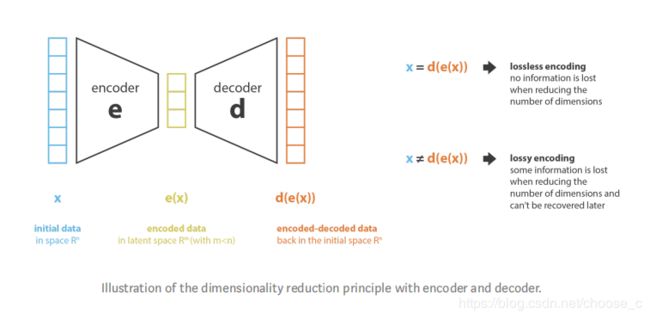
自编码器，降维，PCA

        自编码器(autoencoder)是一种降维的方法，一般的自编码器框架包括了编码器和解码器。编码器通过选择和抽取特征将数据编码到低维隐层特征空间中,解码器则相反。自编码器的损失函数就是编码时最大化信息保留和解码之后最小化重构损失。通过降低隐层特征空间(编码空间)的维度，达到降维的作用。

        说到降维就不得不说PCA(主成分分析)了。PCA中，新的特征是原特征的线性组合，且新特征是相互正交的，目的就是减少信息的丢失。所以pca的编码过程就是求特征空间的特征向量和特征值。PCA也可以融入自编码器框架，编码过程中就是求解编码矩阵，得到编码空间特征向量；解码过程就是进行特征还原，解码矩阵为编码矩阵的转置。线性自编码器其实就是神经网络版的PCA。

        自编码器需要注意的点：①不考虑重构损失的降维，可能会导致缺乏解释性和可开发性。②降维的目的不单单只是减少数据特征的维度，还要得到数据最重要的那些维度。所以最后隐层空间的维度和自编码器的深度需要和降维的目的有关。

变分自编码器

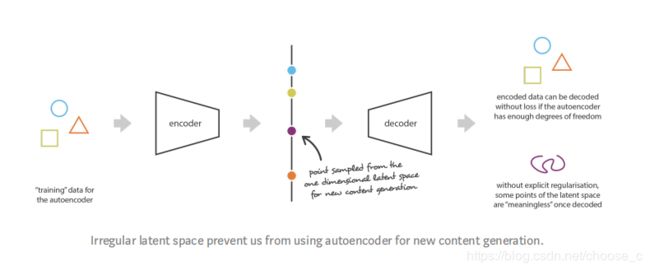
        自编码器和内容生成之间的联系:隐层空间足够“正则化”，就是在编码器训练时well organized。如果自编码器在训练时有足够的自由，那么重构损失会变得很小，在网络足够深时达到0(造成过拟合)。

        变分自编码器的定义：训练时加入正则化防止过拟合，保证隐层空间具有足够的能力进行生成过程的自编码器。所以对自编码器进行了一些轻微的修改：编码过程将输入数据编码成分布而不是一些点。

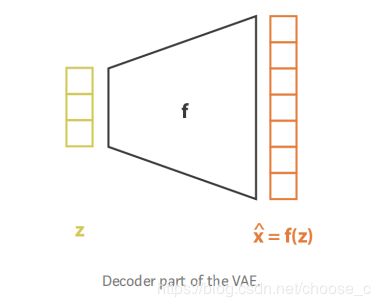
        训练过程：1.将数据编码成分布；2.再从隐层分布中采样数据点；3.解码还原数据并计算重构损失；4.将重构损失反向传播。

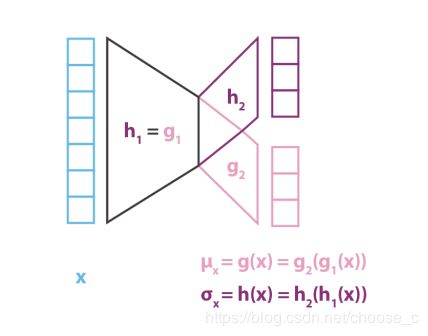
        编码器生成的分布被选为正态分布，那么编码器就可以训练返回描述这些正太分布的均值和协方差矩阵这些统计量就可以。为什么一个输入被编码成分布而不是一个唯一的一点是因为它可以很自然地表达潜在空间的全局正则化和局部正则化，后面会说明这一点：局部是因为方差的控制，全局是因为均值的控制。

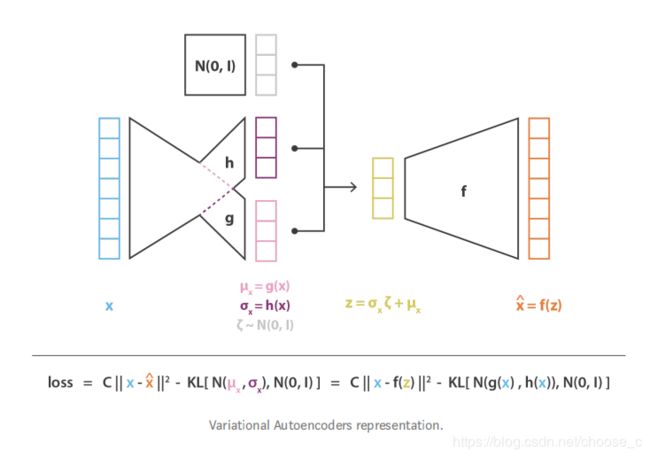
        变分自编码器的损失函数由重构项(最后层)和正则项(隐层)组成。正则项为生成的分布和正太分布之间的KL散度来表示。

直觉上的正则项

        正则化的作用是使隐层空间可以进行生成过程，所以需满足以下两个特点：连续性和完整性。连续性可以理解为隐层中两个相近的点解码后应该近似是一样的；完整性理解为分布中采样得到的点解码后的内容应该是有具体意义的。如果单单是将隐层中的点变成分布是不足以满足上面两个特点。所以需要定义一个好的正则项，即编码器生成的分布接近标准正太分布，协方差矩阵接近单位阵，均值为0。这个正则化项，可以防止模型在潜在空间中对数据进行遥远的编码，并鼓励尽可能多的返回分布“重叠”，从而满足预期的连续性和完整性条件。正则项会提高重构损失，所以训练时需要权衡这两个损失。

VAE的数学细节

          前面的直觉上的总结:VAE是将输入编码成分布的自编码器，并且隐层被规整为标准正太分布。下面从数学的角度来解释这个正则化项的合理性。首先进行如下概率框架定义和假设：

        1.隐层z是从p(z)中采样而来。

        2.数据x是从条件似然分布p(x|z)中采样得到。

        所以在编码器框架中的解码器"条件概率"可以定义为p(x|z),表示给出编码器变量结果下的编码结果的条件分布。编码器“条件概率”p(z|x)。假设z的先验分布p(z)为标准正太分布,那么根据贝叶斯定义：

                                                          

        假设p(z)满足标准正太分布，那么p(x|z)也可以表示为正太分布：

                                                                  

                                                                  

        p(z)和p(x|z)都是满足正太分布的，所以p(z|x)也是满足正太分布的。通过上面的贝叶斯公式，计算p(z|x)是一个标准的贝叶斯推导问题，但是这个计算是很棘手的，因为贝叶斯公式的分母上的积分求解很困难，所以我们需要优化方法，比如变分推断。

变分推断

            变分推断是一个近似复杂分布的技术手段，就是使用一个参数化的分布来寻找目标分布的最优近似。现在我们的目标是近似p(z|x)使用高斯分布q_x(z),它的均值和方差由两个函数g，h定义参数为x。

                                                                 

        所以我们需要找到最优函数解g和h，使得近似分布和目标分布之间KL最小化。         

        从这个倒数第二行的等式中可以看到，在求近似p(z|x)分布时，在可见数据的似然函数最大化(左边项)和先验分布的kl距离最小化(右边项)。这两个权衡项可以理解为对于数据的自信和对先验的自信两者之间的权衡。从倒数第一行的等式中，我们可以得到常数c是权衡左右两项，c越大表示解码器的方差越大，越倾向正则项。

神经网络中变分推断

        从上面可以看出，在神经网络中函数g和h共享同一个结构和权重。

        

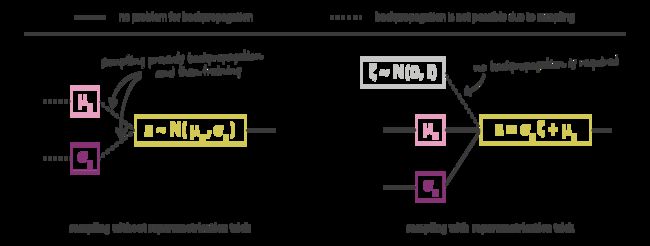
        上面两个图是自编码器神经网络的图，但是训练时变分推断中需要在编码得到的分布中采样得到样本点，但是这个采样过程在训练时无法进行损失的反响传播，所以需要一个重采样的技巧。左边的情况是没有重采样技巧时无法进行反向传播，右边的图表示引入重采样。

         变分自编器的表示总体结构图：

总结

        本文的主要内容：

                1.降维是将描述数据的特征维度数量降低的过程。

                2.自编码器是神经网络架构，通过编码解码过程进行重构，并训练使得重构损失最小。

                3.由于过拟合，自编码器的隐层没有正则化，无法进行生成过程解码得到新数据。

                4.变分自编码器可以解决隐层没有正则化的问题，通过将隐层表示为分布为不是点，并且加入了正则损失。

                5.自编码器的损失由重构和正则损失组成，使用变分推断的方法求解。