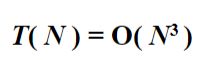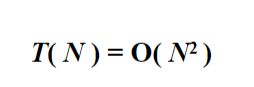MOOC浙大数据结构PAT之实例1.1最大子列和问题
原题链接:https://pintia.cn/problem-sets/434/problems/5404
题目
给定K个整数组成的序列{ N1, N2, ..., NK },“连续子列”被定义为{ Ni, Ni+1, ..., Nj },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据1:与样例等价,测试基本正确性;
- 数据2:102个随机整数;
- 数据3:103个随机整数;
- 数据4:104个随机整数;
- 数据5:105个随机整数;
输入格式:
输入第1行给出正整数K (≤100000);第2行给出K个整数,其间以空格分隔。
输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数,则输出0。
输入样例:
6
-2 11 -4 13 -5 -2
输出样例:
20代码
代码是用Java语言所写,下面的算法是根据MOOC上的老师所教的算法所完成的。
算法1
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 获取输入的正整数
int length = scanner.nextInt();
// 获取要测试的数据,填充到数组中
int[] arrs = new int[length];
for (int i = 0; i < arrs.length; i++) {
arrs[i] = scanner.nextInt();
}
// 打印最大和
System.out.println(maxSum1(length, arrs));
}
private static int maxSum1(int length, int[] arrays) {
// 初始设定最大和为0
int maxSum = 0;
// 这里指的是循环8遍,即数组的长度
for (int i = 0; i < length; i++) {
// 其中j=i表示从第i遍开始加,j maxSum) {
maxSum = thisSum;
}
}
}
return maxSum;
}
}
算法解析:
测试数据:4, -3, 5, -2, -1, 2, 6, -2
第一遍(从第一个数开始加,一共加8次)
4=4
4+(-3)=1
4+(-3)+5=6
4+(-3)+5+(-2)=4
4+(-3)+5+(-2)+(-1)=3
4+(-3)+5+(-2)+(-1)+2=5
4+(-3)+5+(-2)+(-1)+2+6=11
4+(-3)+5+(-2)+(-1)+2+6+(-2)=9
第二遍(从第二个数开始加,一共加7次)
-3=-3
-3+5=2
-3+5+(-2)=0
(-3)+5+(-2)+(-1)=-1
(-3)+5+(-2)+(-1)+2=1
(-3)+5+(-2)+(-1)+2+6=7
(-3)+5+(-2)+(-1)+2+6+(-2)=5
第三遍(从第三个数开始加,一共加6次)
………
第八遍(从第八个数开始加,一共加1次)
-2=-2
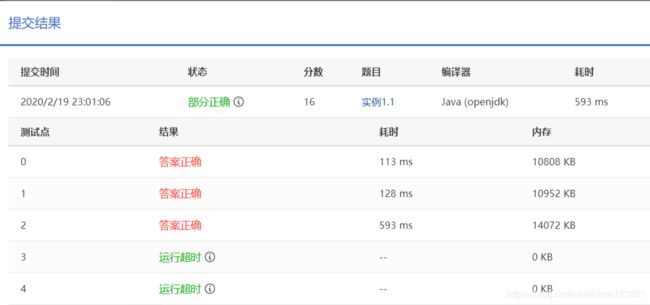
测试结果:
算法2
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 获取输入的正整数
int length = scanner.nextInt();
// 获取要测试的数据,填充到数组中
int[] arrs = new int[length];
for (int i = 0; i < arrs.length; i++) {
arrs[i] = scanner.nextInt();
}
// 打印最大和
System.out.println(maxSum2(length, arrs));
}
private static int maxSum2(int length, int[] arrays) {
// 初始设定最大和为0
int maxSum = 0;
// 这里指的是循环8遍,即数组的长度
for (int i = 0; i < length; i++) {
// 设定此次相加的初始和为0
int thisSum = 0;
// 其中j=i表示从第i遍开始加,j maxSum) {
maxSum = thisSum;
}
}
}
return maxSum;
}
}
算法分析:
测试数据:4, -3, 5, -2, -1, 2, 6, -2
第一遍(从第一个数开始加,下一次相加则从上一次相加结果加上下一项即可)
4=4
4+(-3)=1
1+5=6
6+(-2)=4
4+(-1)=3
3+2=5
5+6=11
11+(-2)=9
第二遍(从第二个数开始加,一共加7次)
-3=-3
-3+5=2
2+(-2)=0
0+(-1)=-1
-1+2=1
1+6=7
7+(-2)=5
第三遍(从第三个数开始加,一共加6次)
………
第八遍(从第八个数开始加,一共加1次)
-2=-2
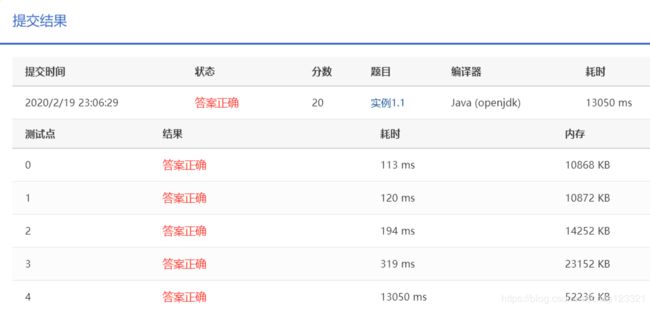
测试结果:
算法3
请参考MOOC浙大数据结构视频。
算法4
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 获取输入的正整数
int length = scanner.nextInt();
// 获取要测试的数据,填充到数组中
int[] arrs = new int[length];
for (int i = 0; i < arrs.length; i++) {
arrs[i] = scanner.nextInt();
}
// 打印最大和
System.out.println(maxSum4(length, arrs));
}
private static int maxSum4(int length, int[] arrays) {
int maxSum = 0, thisSum = 0;
// 循环输入的数组数据
for (int i = 0; i < arrays.length; i++) {
// 计算和
thisSum += arrays[i];
// 判断当前和是否大于最大子数列和
if (thisSum > maxSum) {
// 如果大于则将当前和赋给最大子数列和
maxSum = thisSum;
} else if (thisSum < 0) {
// 如果当前和为负数,就没必要加,不影响后面的和增大
thisSum = 0;
}
}
return maxSum;
}
}
算法分析:
测试数据:4, -3, 5, -2, -1, 2, 6, -2
设定初始最大和maxSum为0
第一步:4+(-3)=1>0,设定maxSum=1
第二步:1+5=6>1,设定maxSum=6
第三步:6+(-2)=4<6,其中maxSum不变
第四步:4+(-1)=3<6,其中maxSum不变
第五步:3+2=5<6,其中maxSum不变
第六步:5+6=11>6,设定maxSum=11
第七步:11+(-2)=9<11,其中maxSum不变
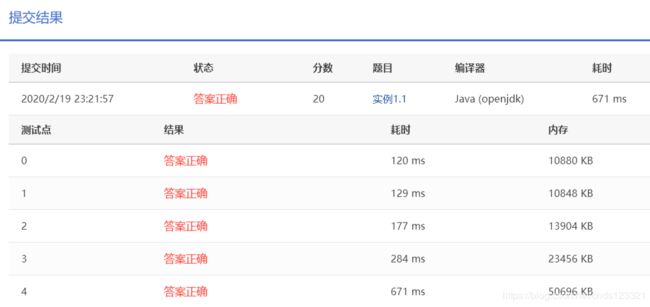
测试结果: