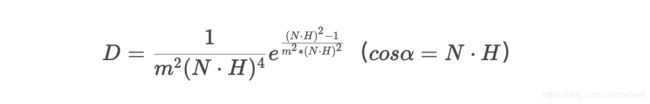【一步步学Metal图形引擎10】-《BRDF:Cook-Torrance光照模型》
教程 10
高级光照模型1:Cook-Torrance BRDF
教程源码下载地址: https://github.com/jiangxh1992/MetalTutorialDemos
CSDN完整版专栏: https://blog.csdn.net/cordova/category_9734156.html
一、关键词
- 基于物理的渲染(PBR)
- 微表面理论
- 能量守恒
- 各向异性
- 菲涅耳反射定律
- 双向反射分布函数BRDF
- 渲染方程(Rendering Equation)
二、原理
之前的传统基础光照模型都是在理想情况下对漫反射和镜面反射现象进行的模拟,不能体现现实中很多特殊材质的性质和光照效果。传统的光照模型是对漫反射和镜面反射采用经验模型来快速高效的简单模拟,实际上跟现实偏离,没有遵守现实中的***能量守恒***,没有考虑***光线的吸收和折射率***,没有考虑到很多物体的***表面的粗糙程度***等等。
2.1 基于物理的渲染(PBR)
PBR(Physically Based Rendering)渲染指的是基于基本的真实物理规律和数学推导,建立模拟真实现象的渲染方程来渲染真实画面的技术。相对于之前传统的基础模拟渲染,PBR渲染开始遵守物理规律,使得渲染更加真实,但由于目前硬件水平等的限制也并没有完全按照现实世界的规律去计算,是介于纯经验算法模拟渲染和真实物理渲染之间的渲染技术。
PBR渲染中加入了能量守恒、菲涅耳反射定律、光的吸收现象等物理规律的考虑,更好的表现物体表面的细节和粗糙度,各向异性,区分金属和非金属材质,半透明材质等各种复杂的材质特性。
2.2 微表面理论
微表面理论指的是,认为物体表面由于粗糙程度不同,会不同程度上分布有朝向不一的微小平面。传统基础光照模型是在理想情况下,认为物体表面是光滑的。而微表面理论下,实际上任何物体表面都不会是完全光滑的。
微表面理论下的微表面细小到无法在像素层次对其进行细分描述,所以是假设了一个理论上的粗糙度的量(Roughness)来从统计学上对其进行估算描述。
那么在微表面理论下,之前Blinn-Phong模型高光计算中的半角向量H,对微表面法线的平均取向有一定表达意义,是微表面理论下一个重要的中间变量。
![]()
2.3 能量守恒
PBR渲染中光照的计算不仅仅是漫反射和镜面反射那么简单,而是基于能量守恒来大体分析光线的传播过程。光线照在物体表面,一部分成为反射光,一部分成为折射光,反射光强的比例遵守菲涅耳反射定律。反射光和折射光的总和按照能量守恒等于入射光的强度。
另外折射光进入物体表面,一部分被物体吸收,一部分可能经过内部多次弹射再次射出物体表面称为漫射光。因此漫射光的比例与反射光的比例之和肯定不大于1.0,因为还有被物体吸收的光。
2.4 BRDF与渲染方程
BRDF,双向反射分布函数,描述的是对于特定粗糙表面,从方向wi入射的光在w0方向上的反射光比例。在理想的光滑物体表面,反射光方向是和入射光方向关于法线对称的,但是实际上物体表面不可能完全光滑,所以反射光会在不同的方向上散射,而不是只集中在关于法线对称的那一个方向上。
如下图,左边是之前我们理想情况下的镜面反射,右边才是实际上镜面反射的现象,反射光会向不同的方向散射开来,而BRDF就描述了不同的方向上反射光占总反射光的比例,因此BRDF是一个不大于1.0的比例系数。
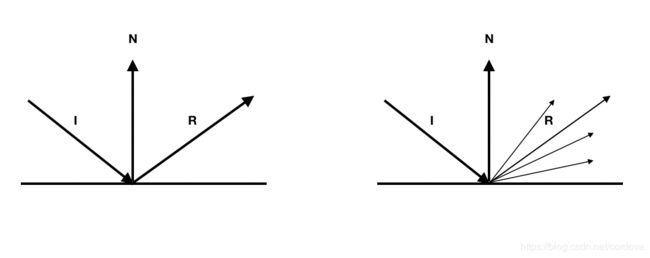
因此之前理想情况下的Phong模型中,我们漫反射和镜面反射的BRDF是一种理想的极特殊情况,反射光集中在反射方向R上,只有当反射方向为R时BRDF为1.0,其他方向BRDF都为0。
渲染方程是一个通用情况下描述光照的数学模型,由Kajia在1986年提出。不考虑自发光公式如下:

其中x表示入射点;Lo(x,wo)表示的是光线从物体表面点x沿方向wo反射的光强;fr(x,wi,wo)表示的就是入射光方向为wi,照射到点x然后在wo方向上反射的BRDF;
Li(x,wi)是沿wi方向入射到点x的光线的光照强度;n表示点x处的法线;
最后在不同的反射方向wi上进行积分就是所有反射光强的总和Lo。
这里只需要分析镜面反射,实际上漫反射也适用BRDF的反射分布,但漫反射的BRDF值在各个方向上的值都是恒定的,可以忽略不计。
BRDF遵守能量守恒,各个方向上的反射光强总和不会超过入射光的强度。
2.5 Cook-Torrance光照模型
通过前面的分析我们知道Phong和Blinn-Phong光照模型都是理想情况下的简单光照模拟,和现实不一致,没有考虑不同材质的特性,效果过于艺术化,不真实。
Cook-Torrance模型中开始考虑微表面的存在,加入表面粗糙度的考量。模型中还是将光照分为漫反射和镜面反射,其中漫反射跟之前的依然相同,只是镜面反射系数的计算更加复杂。可见Cook-Torrance和Phong以及Blinn-Phong的计算都仅仅是高光系数不同,公式形式都类似如下:
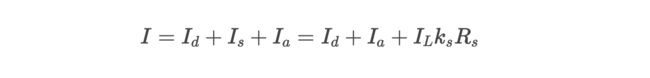
其中Id是漫反射光,Ia是环境光,IL是平行光的光强,ks是镜面反射系数,而Rs则是我们的高光项:specular term。Rs在Phong模型中为:(R · V)^n,在Blinn-Phong中为:(N · H)^n,而在Cook-Torrance模型中Rs的计算公式为:
- F项是菲涅耳反射系数(Fresnal reflect term),表示反射光强占入射光强的比例。这里计算F的一个近似公式为:

其中f0为入射角度接近0也就是入射方向和法线接近重合时的菲涅耳反射系数,这个系数要我们根据材质特性来进行测量设置;V是视线方向;H为半角向量。
- D项是微表面分布函数,计算的是“给定方向上的微平面的分数值”,一个统计学的衡量。这里我们计算的是在半角向量H上的微平面分布分数值。常用的微平面分布函数是Backmann分布函数:

其中m(0~1)用来度量物体表面的粗糙度,m越大表面越粗糙;角度alpha是顶点法向量N和半角向量H的夹角,公式变换可得到最终的Backmann微平面分布函数为:
- G项是几何衰减系数,用来衡量由于表面凹凸不平导致相邻微平面互相遮挡对光强的影响。G项的计算公式为:

其中当未被遮挡时光强为1,另外两种情况分别是入射光部分被遮挡和反射光部分被遮挡,G项定义为这三种情况中光强最小的那个。
三、源码分析
3.1 Render.m
// ...
uniforms->f = 0.015;
uniforms->m = 0.8;
// ...
Uniform Buffer中加入两个变量,一个是菲涅耳系数f,一个是粗糙度m,每一帧开始前在updateGameState函数中设置。
3.2 Shaders.metal
Shader中我们在fragment函数中进行Cook-Torrance镜面反射系数Rs的计算。
// ...
float Rs = 0;
float nv = dot(N, V);
float nl = dot(N, L);
bool front = (nv > 0) && (nl > 0); // 正面
// ...
Rs我们默认设为0。另外我们要保证光线和视角都在物体的正面,即法线所在的那一面。另一面我们的Rs为默认的0。
// ...
if(front)
{
float nh = dot(N, H);
float vh = dot(V, H);
// F
float F = uniforms.f + (1 - uniforms.f) * pow(1 - vh, 5.0);
// D
float temp = (nh * nh - 1) / (uniforms.m * uniforms.m * nh * nh);
float D = exp(temp) / (uniforms.m * uniforms.m) * pow(nh, 4.0);
// G
float G1 = (2 * nh * nv) / vh;
float G2 = (2 * nh * nl) / vh;
float G = fmin3(1.0, G1, G2);
// Rs
Rs = (F * D * G) / (nv * nl);
}
// ...
根据Cook-Torrance的光照公式计算出我们的specular term系数。
// ...
// Specular(cook-torrance)
float specular = uniforms.IL * uniforms.Ks * Rs;
// ...
最后将镜面反射部分的系数替换为我们计算的Rs即可。
// ...
half4 color_sample = half4(0,0.7,0.2,1.0);//baseColorMap.sample(linearSampler,in.texCoord.xy);
// ...
另外我们将模型的材质设置为一个翠绿色,近似模拟出玉石的材质效果,效果图见下图。
四、运行效果
参考文章:
由浅入深学习PBR的原理和实现
《GPU编程与CG语言之阳春白雪与下里巴人》