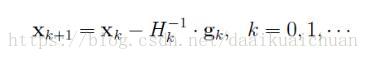优化算法之梯度下降法、牛顿法、拟牛顿法和拉格朗日乘数法

  在机器学习中，优化方法是其中一个非常重要的话题，最常见的情形就是利用目标函数的导数通过多次迭代来求解最优化问题。

- 无约束最优化问题：梯度下降法、牛顿法、拟牛顿法；
- 有约束最优化问题：拉格朗日乘数法。

一、梯度下降法

1、算法简介

  梯度下降法是最早最简单，也是最为常用的最优化方法。梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向（梯度方向是上升最快的方向）作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近目标值，步长越小，前进越慢。梯度下降法的搜索迭代示意图如下图所示：

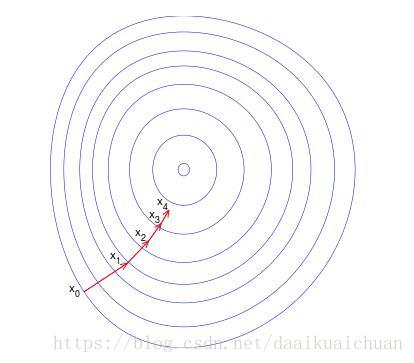
2、算法流程

核心迭代公式为 ：

  其中，pk（dk）是第k次迭代时选取的移动方向，在梯度下降法中，移动的方向设定为负梯度方向。 ak（λk）是第k次迭代是移动的步长或者叫学习率，每次移动的步长可以固定也可以改变。因此，梯度下降法计算步骤可以概括为 ：

3、算法总结

  实际上，梯度还可以提供不在最快变化方向的其他方向上坡度的变化速度，即在二维情况下，按照梯度方向倾斜的圆在平面上投影成一个椭圆。椭球面的形状受 Hesse 矩阵的条件数影响，椭球面越扁，那么优化路径需要走很大的弯路，计算效率很低。这就是常说的锯齿现象（ zig-zagging），将会导致收算法敛速度变慢。

梯度下降法的缺点：

1. 靠近极小值时收敛速度减慢；

2. 直线搜索时可能会产生一些问题；

3. 可能会“之字形”地下降。

4、随机梯度下降法（SGD）

  随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。对应的更新公式是：

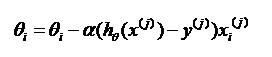
  对于每一次更新参数，不必遍历所有的训练集合，仅仅使用了一个数据，来变换一个参数。这样做不如完全梯度下降的精确度高，可能会走很多弯路，但整体趋势是走向minmum。这样做可以节省更多的时间，算法更快。
  那么为什么叫随机梯度下降算法呢？这里的随机是指每次迭代过程中，样本都要被随机打乱，这个也很容易理解，打乱是有效减小样本之间造成的参数更新抵消问题。

void Logistic::stocGradAscent()
{
    double alpha = 0.01;
    double h = 0.0;
    int i = 0;
    int j = 0;
    double error = 0.0;
    vector<int> randIndex;
    for (i = 0; i < trainMat.size(); ++i)
        randIndex.push_back(i);
    for (int k = 0; k < numIter; ++k)
    {
        //每次迭代过程中，样本都要被随机打乱，这个也很容易理解，
        //打乱是有效减小样本之间造成的参数更新抵消问题。
        random_shuffle(randIndex.begin(), randIndex.end());
        for (i = 0; i < trainMat.size(); ++i)
        {
            //随着迭代的步骤增多，学习率通常要逐渐减小，这样可以有效避免训练中出现误差震荡情况。
            alpha = 4 / (1 + k + i) + 0.01;
            h = sigmoid(scalarProduct(trainMat[randIndex[i]], weight));
            error = trainLabel[randIndex[i]] - h;
            for (j = 0; j < weight.size(); ++j)
            {
                weight[j] += alpha * error * trainMat[randIndex[i]][j];
            }
        }
    }
}

二、牛顿法

  一般来说, 牛顿法主要应用在两个方面：1, 求方程的根; 2, 最优化。

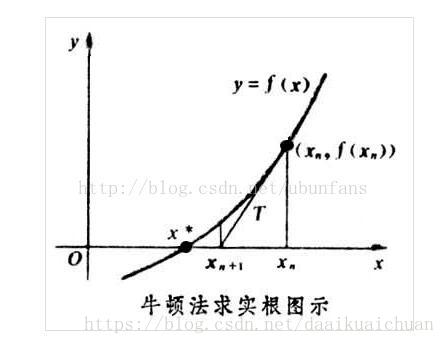
1、求方程的根

2、最优化

（1）算法简介

  牛顿法是利用局部的一阶和二阶偏导信息，去推测整个目标函数的形状，进而可以求得近似函数的全局最小值，然后将当前的最小值设定为近似函数的最小值。也就是说，牛顿法在二阶导数的作用下，从函数的凸性出发，直接搜索怎样到达极值点，即在选择方向时，不仅考虑当前坡度是否够大，还会考虑走了一步之后，坡度是否会变得更大。

  最终的迭代公式为：

（2）算法流程

（3）算法总结

  牛顿法是梯度下降法的发展，梯度法利用目标函数的一阶偏导数，以负梯度方向作为搜索方向，只考虑了局部信息。而牛顿法不仅使用目标函数的一阶偏导，还进一步利用了二阶偏导，这样就考虑了梯度变化的趋势，因而收敛速度更快。

牛顿法的缺点：

1. 对目标函数有较为严格要求，函数必须具有连续的一、二阶偏导数，海森矩阵必须正定；

2. 计算相当复杂，除需要计算梯度外，还需要计算二阶偏导数和它的逆矩阵，计算量和存储量很大。

三、拟牛顿法

1、算法简介

  拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。常用的拟牛顿法有DFP算法和BFGS算法。

2、算法流程

四、拉格朗日乘数法

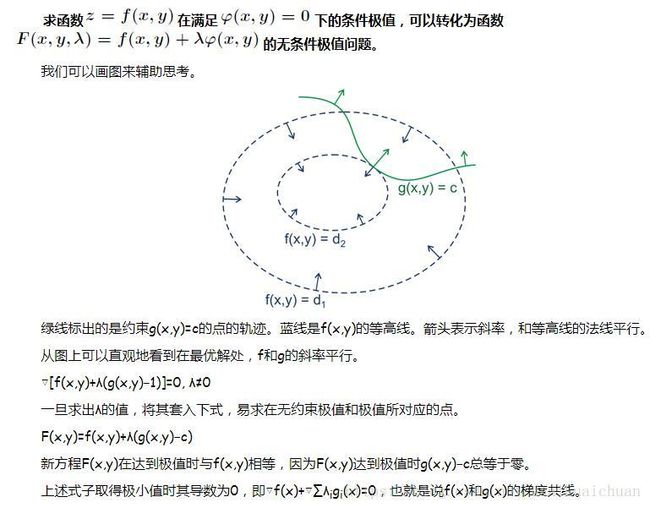
1、拉格朗日乘子

  作为一种优化算法，拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。

2、KKT条件

3、拉格朗日对偶性

（1）原始问题

（2）对偶问题

（3）原始问题与对偶问题的关系

1. 如果原问题是强对偶问题（凸二次规划问题是强对偶），则原始问题的解等价于对偶问题的解；

2. 如果可行解满足KKT条件，则原始问题的解等价于对偶问题的解。

参考：https://blog.csdn.net/itplus/article/details/21896453
https://blog.csdn.net/majinlei121/article/details/47260917
https://blog.csdn.net/luanpeng825485697/article/details/79674610
https://www.cnblogs.com/shixiangwan/p/7532830.html
https://blog.csdn.net/ubunfans/article/details/41520047
https://blog.csdn.net/lipengcn/article/details/52698895
https://blog.csdn.net/sinat_17496535/article/details/52103852