最优化算法之模拟退火算法(SA)
一、爬山算法 ( Hill Climbing )
介绍模拟退火前,先介绍爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
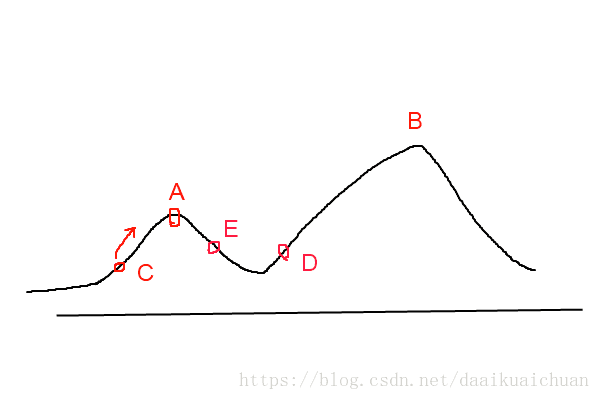
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如图1所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
二、模拟退火算法(SA)
1、退火的概念
在热力学上,退火(annealing)现象指物体逐渐降温的物理现象,温度愈低,物体的能量状态会低;够低后,液体开始冷凝与结晶,在结晶状态时,系统的能量状态最低。大自然在缓慢降温(亦即,退火)时,可“找到”最低能量状态:结晶。但是,如果过程过急过快,快速降温(亦称「淬炼」,quenching)时,会导致不是最低能态的非晶形。
如下图所示,首先(左图)物体处于非晶体状态。我们将固体加温至充分高(中图),再让其徐徐冷却,也就退火(右图)。加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小(此时物体以晶体形态呈现)。
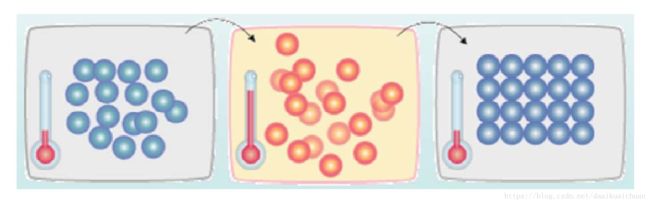
似乎,大自然知道慢工出细活:缓缓降温,使得物体分子在每一温度时,能够有足够时间找到安顿位置,则逐渐地,到最后可得到最低能态,系统最安稳。
2、模拟退火(Simulate Anneal)的概念
想象一下如果我们现在有下面这样一个函数,现在想求函数的(全局)最优解。如果采用Greedy策略,那么从A点开始试探,如果函数值继续减少,那么试探过程就会继续。而当到达点B时,显然我们的探求过程就结束了(因为无论朝哪个方向努力,结果只会越来越大)。最终我们只能找打一个局部最后解B。

模拟退火其实也是一种Greedy算法,但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。以上图为例,模拟退火算法在搜索到局部最优解B后,会以一定的概率接受向右继续移动。也许经过几次这样的不是局部最优的移动后会到达B 和C之间的峰点,于是就跳出了局部最小值B。
【总结】:
- 若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解),则总是接受该移动;
- 若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差),则以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)相当于上图中,从B移向BC之间的小波峰时,每次右移(即接受一个更糟糕值)的概率在逐渐降低。如果这个坡特别长,那么很有可能最终我们并不会翻过这个坡。如果它不太长,这很有可能会翻过它,这取决于衰减 t 值的设定。
3、模拟退火算法伪代码
/*
* J(y):在状态y时的评价函数值
* Y(i):表示当前状态
* Y(i+1):表示新的状态
* r: 用于控制降温的快慢
* T: 系统的温度,系统初始应该要处于一个高温的状态
* T_min :温度的下限,若温度T达到T_min,则停止搜索
*/
while( T > T_min )
{
dE = J( Y(i+1) ) - J( Y(i) ) ;
if ( dE >=0 ) //表达移动后得到更优解,则总是接受移动
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
else
{
// 函数exp( dE/T )的取值范围是(0,1) ,dE/T越大,则exp( dE/T )也
if ( exp( dE/T ) > random( 0 , 1 ) )
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
}
T = r * T ; //降温退火 ,0
/*
* 若r过大,则搜索到全局最优解的可能会较高,但搜索的过程也就较长。若r过小,则搜索的过程会很快,但最终可能会达到一个局部最优值
*/
i ++ ;
} 4、模拟退火算法的步骤
1. 初始化温度T,初始解状态S,每个温度t下的迭代次数L;
2. 当k = 1,2,……,L时,进行3~6;
3. 对当前解进行变换得到新解S’(例如对某些解中的元素进行互换,置换);
4. 计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数;
5. 若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/(KT))接受S′作为新的当前解(k为玻尔兹曼常数,数值为:K=1.3806505(24) × 10^-23 J/K);
6. 如果满足终止条件则输出当前解作为最优解,结束程序;
7. 减小T,转到第2步,直到T小于初始设定的阈值。
5、模拟退火算法的优缺点
- 迭代搜索效率高,并且可以并行化;
- 算法中有一定概率接受比当前解较差的解,因此一定程度上可以跳出局部最优;
- 算法求得的解与初始解状态S无关,因此有一定的鲁棒性;
- 具有渐近收敛性,已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法。
6、模拟退火算法的demo
#include 参考:https://blog.csdn.net/qq_30981697/article/details/70032094?locationNum=9&fps=1
https://blog.csdn.net/baimafujinji/article/details/52573630
http://blog.jobbole.com/108559/
https://blog.csdn.net/baimafujinji/article/details/6474567
https://blog.csdn.net/google19890102/article/details/45395257
