写这篇 文章 的 原因 是 网友 水星之魅 在 反相吧 发了一个 帖 《知乎问题,Newton 如果穿越到现在,他会怎样?》 https://tieba.baidu.com/p/6699008721 ,
我就去 知乎 上 找 这个 问题 看, 结果 这个 问题 没找到, 找到了 另外一个 问题 《牛顿如果穿越到现在,能看懂相对论和量子力学吗?》 https://www.zhihu.com/question/318014039/answer/645620511 。
这个问题中, 网友 的 回答 中 提到 :
“
牛顿晚年时面对杰出年轻后辈约翰伯努利深入研究过的最速降线的挑战一夜之间就给出答案这是什么概念!!后来牛顿在与朋友通信提到此事时曾经说过“我最讨厌有人在数学上挑衅我!”
”
看到 这段话, 我不禁 莞尔一笑 。
传说, 牛顿 一个晚上 就 搞定了 最速降线 。
从 欧拉-拉格朗日 方程 的 推导过程 可以看到, 推导 欧拉-拉格朗日 方程 需要 完整成熟 的 微积分计算体系, 根据 欧拉-拉格朗日 方程 推导出 最速降线 需要 解 微分方程 。 见 《最速降线的数学模型—变分法》 https://www.jianshu.com/p/961e890e88b2 。
有没有 牛顿 推导 最速降线 的 手稿 和 推导方法 ? 可以 拿来 看一看 。
天辩阮幼台 (陈彼方) skywalkerwyj (青莲剑歌)
欧拉-拉格朗日 方程 描述 的 问题场景 是, 对于 二维平面 上 2 点 间 的 一段 曲线, 以 这段 曲线 作为 积分路径, 作 某个 定积分, 问 曲线 是 什么样 时, 定积分 值 最小 ? 或者说, 求 定积分 值 最小 时 的 曲线(曲线方程) 。
寻找 三维空间 里的 曲面 上 的 2 点 间 的 最短距离线(短程线) 也是 一个 泛函问题 。
寻找 曲面 上 的 2 点 间 的 最速降线 也是 一个 泛函问题 。
曲面 上 2 点 间 的 短程线 不一定是 最速降线, 反之亦然 。
有没有 可能 曲面 的 短程线 和 最速降线 是 同一条线 ? 还是 永远不可能 ? 嗯, 这是个 问题 。
曲面 上 的 最速降线 是 什么? 似乎 要 解释一下 。 对于一个 曲面, 在 曲面 上 取 2 点, 在 2 点 间 在 曲面 上 画 一条线, 让 小球 沿着 这条线 在重力下滚动, 小球 从 一个点 最快 滚动 到 另一个 点 的 那条线, 就是 曲面 的 最速降线 。
通过 对 最速降线(包括 二维平面 和 三维曲面 的) 和 短程线 的 一些 研究, 可以看到, 泛函问题 涉及 到 某种 “整体规划” 。 如果 没有 “整体规划”, 那么 泛函问题 就 退化 为 普通 的 微积分问题, 比如, 函数极值问题 、一般 的 微分方程 问题 、一般 的 级数问题 。
也可以说, 整体规划 是 泛函问题 的 一个 重要特征 。
因为 整体规划 的 关系, 我有一个 大胆 的 想法, 在 变分法 出现 以前, 纯数学 解决 最速降线 问题 是 不可能 的 。
在《最速降线问题》 https://www.cnblogs.com/lfri/p/10327570.html 中, 介绍了 伯努利 利用 费马原理 和 斯涅耳定理 来 证明 最速降线 的 方法 。
那是 一个 巧妙 的 方法, 也捎带了 人们 主观 的 美好愿望 。
为了 便于 叙述, 我们 把 伯努利 利用 费马原理 和 斯涅耳定理 来 证明 最速降线 的 方法 称为 伯努利推导法 。
伯努利推导法 是这样的, 根据 斯涅耳定理 (折射定律) :
sin θ1 / v1 = sin θ2 / v2
于是, 对于 每一次 入射(折射), 可得 :
sin θ / v = C1 , C1 为 常量 (1) 式
下一次 的 入射角 等于 上一次 的 折射角, 把 每一次 入射(折射) 看作 微元, 每一个 微元 都 满足 (1) 式 的 曲线 就是 最速降线 。
设 曲线 是 y = p (x) , 曲线 的 导数 是 y ′ , 导数 是 曲线 上 一点 的 切线, 也就是 该点 微元 的 折射光 的 方向, (1) 式 中 的 θ 就是 折射角,
ctg θ = y ′
sin θ = 1 / 根号 ( 1 + y ′ ² )
代入 (1) 式, 得 :
[ 1 / 根号 ( 1 + y ′ ² ) ] / v = C1 (2) 式
根据 机械能守恒, 可知 v = 根号 ( 2 g y ) , 代入 (2) 式, 得 :
[ 1 / 根号 ( 1 + y ′ ² ) ] / 根号 ( 2 g y ) = C1
1 / [ 根号 ( 1 + y ′ ² ) * 根号 ( 2 g y ) ] = C1
1 / [ 根号 ( 1 + y ′ ² ) * 根号 ( y ) ] = C1 * 根号 ( 2 g )
根号 ( 1 + y ′ ² ) * 根号 ( y ) = 1 / [ C1 * 根号 ( 2 g ) ]
令 C2 = 1 / [ C1 * 根号 ( 2 g ) ] , 因为 C1 、g 是 常量, 所以 C2 也是 常量,
根号 ( 1 + y ′ ² ) * 根号 ( y ) = C2 (3) 式
(3) 式 就是 最速降线 的 微分方程, 解出 (3) 式 就可以得到 最速降线 的 曲线方程 。
(3) 式 和 用 变分法 欧拉-拉格朗日 方程 第二种形式 得到 的 微分方程 是 一样 的 , 见 《最速降线的数学模型—变分法》 https://www.jianshu.com/p/961e890e88b2 。 文章 里 还有 解 这个 微分方程 的 过程 。
伯努利推导法 并没有 证明 推导出 的 “最速降线” (摆线) 是 小球 滚动 时间 最短 的 路径 。
我上面说过 泛函 的 重要特征 是 整体规划, 用 直观 和 逻辑 分析一下 可以知道, 最速降线 的 构造 也 需要 整体规划, 局部 的 最速 不代表 整体 的 最速 。
但是, 伯努利推导法 根据 每个微元 最速 推导出 的 整体 也是 最速, 这也许 是 一个 有趣 的 巧合 。
也就是说, 在 最速降线 问题 上, 任意 一个 局部 的 最优 等价于 整体 的 最优, 这也许 反映了 某种 全息 ?
伯努利推导法 的 依据 是 费马原理 和 斯涅耳定理, 费马原理 认为 光 总是 沿着 所需 时间 最少 的 路径 前进, 但是 费马原理 是 一个 原理, 差不多是一个 公设, 它有一些 实验支持, 更多的是表达了 人们 主观 的 愿望 和 想象 。
理论上, 伯努利推导法 并没有 给出 “最速降线”(摆线) 是 最速降线 的 证明 。
我原来还 怀疑 费马原理 是否 成立, 试了一下, 还真可以 推导出 折射定律(斯涅耳定理) 。
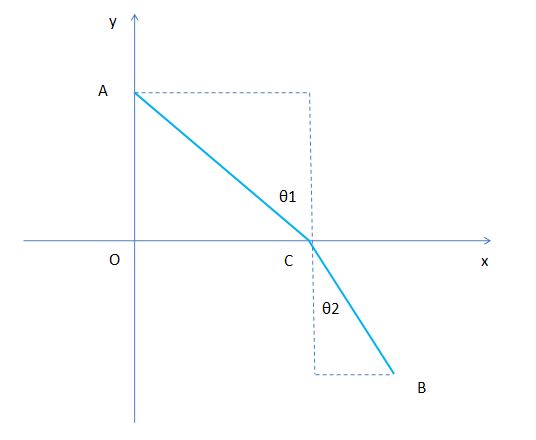
如图, 光线 从 A 点 出发, 沿 AC 以 速度 v1 到达 C 点, 又 从 C 点 以 速度 v2 沿 CB 到达 B 点, C 点 在 x 轴 上, 问 C 点 的 横坐标 是 多少时, 光 沿 AC - CB 的 路径 从 A 到 B 所用 的 时间 最短 ?
设 A 点 坐标 是 ( 0, h1 ), B 点 坐标 是 ( L, h2 ) , C 点 坐标 是 ( x, 0 ) ,
AC = 根号 ( x ² + h1 ² )
BC = 根号 [ (L - x) ² + h2 ² ]
从 A 到 B 的 时间 t = AC / v1 + BC / v2
t = 根号 ( x ² + h1 ² ) / v1 + 根号 [ (L - x) ² + h2 ² ] / v2 (4) 式
(4) 式 中 x 为 自变量, h1, h2, L, v1, v2 为 常量 。
接下来 就是 求 t 的 最小值 发生在 什么时候, 这是一个 极值问题 。 函数极值 出现在 极值点 和 折点 。
极值点 是 导数 为 0 的 点, 且 点 的 两边 的 导数 异号 。
折点 是 导数 为 无穷, 但 函数值 不是 无穷, 且 点 的 两边 的 导数 异号 的 点 。 折点 也可以 称为 不光滑极值点 。
还有一种情况 是 单边折点, 单边折点 是 导数 为 无穷, 函数值 不是 无穷, 且 只在 点 的一边 有 函数, 另一边 没有 函数 的 点 。
比如, y = 根号 ( x ) , 当 x = 0 时, y = 0 , y ′ = 无穷 , 当 x >= 0 时, y 存在, 当 x < 0 时, y 不存在 。
所以, x = 0 是 y = 根号 ( x ) 的 单边折点 。
这里 只 考虑 极值点, 即 导数 为 0 的 情况, 简单一点, 点 的 两边 导数 是否 异号 也略去 不考虑 。
先求 t 的 导数,
t ′ = [ 根号 ( x ² + h1 ² ) / v1 + 根号 [ (L - x) ² + h2 ² ] / v2 ] ′
= 1 / v1 * 1/2 * 1 / 根号 ( x ² + h1 ² ) * 2x + 1 / v2 * 1/2 * 1 / 根号 ( (L - x) ² + h2 ² ) * ( 2x - 2L )
= 1 / v1 * x / 根号 ( x ² + h1 ² ) + 1 / v2 * ( x - L ) / 根号 ( (L - x) ² + h2 ² )
= 1 / v1 * x / 根号 ( x ² + h1 ² ) - 1 / v2 * ( L - x ) / 根号 ( (L - x) ² + h2 ² )
t ′ = 1 / v1 * x / 根号 ( x ² + h1 ² ) - 1 / v2 * ( L - x ) / 根号 ( (L - x) ² + h2 ² ) (5) 式
简单的分析一下, 若 v1, v2 不为 0 , 则 h1, h2, L, x 无论 取 什么值, (5) 式 都不会 是 无穷 , 所以 只要 看 t ′ = 0 的 情况 就可以 。
1 / v1 * x / 根号 ( x ² + h1 ² ) - 1 / v2 * ( L - x ) / 根号 ( (L - x) ² + h2 ² ) = 0
1 / v1 * x / 根号 ( x ² + h1 ² ) = 1 / v2 * ( L - x ) / 根号 ( (L - x) ² + h2 ² )
可以看到,
x / 根号 ( x ² + h1 ² ) = sin θ1
( L - x ) / 根号 ( (L - x) ² + h2 ² ) = sin θ2
于是,
1 / v1 * sin θ1 = 1 / v2 * sin θ2
sin θ1 / v1 = sin θ2 / v2 (6) 式
(6) 式 就是 折射定律 (斯涅耳定理) 。
看起来, 费马原理 在 折射 时 是 成立 的, 也可以说, 折射定律 选择 的 路径 是 最速路径 。
伯努利推导法 把 一次 折射 看作 一个 微元, 由上可知, 每个 微元 是 一个 最速路径, 但 由 这些 微元 构成 的 曲线 是不是 最速路径 ? 不知道 。 这需要 证明 。
还可以 发现一件事, 来看 两个 场景 。
场景一 :
前提 :
sin θ / v = C , C 为常量
v = V ( y )
推论 :
sin θ = 1 / 根号 ( 1 + y ′ ² )
sin θ / v = 1 / 根号 ( 1 + y ′ ² ) / V ( y ) = C
1 / [ 根号 ( 1 + y ′ ² ) * V ( y ) ] = C
根号 ( 1 + y ′ ² ) * V ( y ) = 1 / C (7) 式
场景二 :
前提 :
在 最速降线 问题 中, 设 最速降线 是 y = p ( x ) 。
由 机械能守恒 可知, v = 根号 ( 2 g y ) , 一般的, 若 v 只和 y 有关系, 可以 写成 v = V ( y ) 。
推论 :
y = p ( x ) 的 曲线微元 ds = 根号 ( 1 + y ′ ² ) dx
小球 经过 每个 曲线微元 的 时间 dt = ds / v
小球 在 y = p ( x ) 曲线 上 从 x1 处 滚动 到 x2 处 所用的 时间 t = ʃ dt = ʃ ds / v = ʃ 根号 ( 1 + y ′ ² ) dx / v
= ʃ 根号 ( 1 + y ′ ² ) / v dx
= ʃ 根号 ( 1 + y ′ ² ) / V ( y ) dx
t = ʃ 根号 ( 1 + y ′ ² ) / V ( y ) dx
令 F = 根号 ( 1 + y ′ ² ) / V ( y ) ,
欧拉-拉格朗日方程 第二种形式 :
∂ F / ∂ x - d ( F - y ′ * ∂ F / ∂ y ′ ) / dx = 0
把 F 代入 欧拉方程, 因为 F = 根号 ( 1 + y ′ ² ) / V ( y ) , F 和 x 无关, 所以, ∂ F / ∂ x = 0 , 于是,
d ( F - y ′ * ∂ F / ∂ y ′ ) / dx = 0
F - y ′ * ∂ F / ∂ y ′ = C , C 为 常量
根号 ( 1 + y ′ ² ) / V ( y ) - y ′ * 1/2 * 1 / 根号 ( 1 + y ′ ² ) * 2 * y ′ / V ( y ) = C
根号 ( 1 + y ′ ² ) / V ( y ) - y ′ ² / [ 根号 ( 1 + y ′ ² ) * V ( y ) ] = C
( 1 + y ′ ² - y ′ ² ) / [ 根号 ( 1 + y ′ ² ) * V ( y ) ] = C
1 / [ 根号 ( 1 + y ′ ² ) * V ( y ) ] = C
根号 ( 1 + y ′ ² ) * V ( y ) = 1 / C (8) 式
(7) 式 和 (8) 式 相同 。 (7) 式 (8) 式 就是 最速降线 的 微分方程, 它 的 解 就是 最速降线 的 曲线方程 。
场景一 是 伯努利推导法, 场景二 是 用 变分法 解 最速降线 问题 , 可以看到, (7) 式 和 (8) 式 是 一样 的, 就是说, 场景一 和 场景二 推出 的 是 一样 的 结果 。
场景一 和 场景二 推出 一样 的 结果 说明了什么 ? 是 一个 奇妙 的 巧合 ? 还是 隐藏了 什么 神奇 的 自然原理 ?
在 《最速降线的数学模型—变分法》 的 结尾 提到 : “最速降线的运动时间T全部都是常量,即与物体的初始位置无关。 最速降线也称之为等时降线。”
我在 上文 中 也 提到 “在 最速降线 问题 上, 任意 一个 局部 的 最优 等价于 整体 的 最优” 。
等时 和 局部整体最优等价 这 两者 之间 有什么关系 ?
从 场景一 和 场景二 中, 我们 可以 总结出 一个 规律: 只要 满足 v = V ( y ) , v 和 x 无关, 只 和 y 有关, 且 dt = ds / v , 则 最速路径 就 满足 sin θ / v = C , C 为常量 。
一般的, 对于 二维平面 上 的 运动, 总是有: ds = 根号 ( 1 + y ′ ² ) dx , dt = ds / v , t = ʃ 根号 ( 1 + y ′ ² ) / V ( y ) dx
所以, 可以 进一步 总结为, 只要 满足 v = V ( y ) , v 和 x 无关, 只 和 y 有关, 则 二维平面 上 的 最速路径 就 满足 sin θ / v = C , C 为常量 。
这个规律 可以 称为 二维平面 上 最速路径 的 y 法则 。
在 场景二 里 , 有这样一句话 “ 因为 F = 根号 ( 1 + y ′ ² ) / V ( y ) , F 和 x 无关, 所以, ∂ F / ∂ x = 0 ” ,
“ F 和 x 无关, 所以, ∂ F / ∂ x = 0 ” , 这是一个 简略 的 说法 。
比较 完整 的 应该是 “ F 在 形式 上 和 x 无关, 所以, ∂ F / ∂ x = 0 ” 。
∂ F / ∂ x 这个 偏导数 在 这里 可以认为是 不考虑 x 和 y 、y ′ 的 关系, 仅从 F 函数式 的 层面 来 取 F 和 x 的 导数关系, 而 F 函数式 中 没有 x, 可以认为 在 F 层面, F 和 x 无关, 可以认为, 对于 x , F 是 常量 。 于是, ∂ F / ∂ x = dC / dx = 0 / dx = 0 。
如果反过来, 认为, 对于 F , x 是 常量 呢 ? ∂ F / ∂ x = dF / dC = dF / 0 = 无穷 。 这有点尴尬 。
如果认为 F 和 x 都是 常量 ? ∂ F / ∂ x = dC / dC = 0 / 0 = 1 。 这也不对 。
变分法(欧拉-拉格朗日 方程) 是 找到了 一种 对 曲线积分 进行 整体规划 的 数学方法 。 它 的 解 是 一条 最优路径 。
我对 变分法 还没有 仔细研究, 但 大概 应该是 这样 的 。
又 因为 数学的界限, 我又有 一个 大胆 的 想法, 欧拉-拉格朗日 方程 是 纯数学 解 泛函问题 的 登顶之作 。
有关 数学的界限, 见 《从 三江方士 的 中华级数 想到 数学的界限》 https://www.cnblogs.com/KSongKing/p/11160645.html 。
泛函 和 三体 是 数学 的 两大问题, 这两个 问题 和 工业体系 和 科技树 关系密切 。
关于 泛函, 我之后会写一篇文章 《离散泛函》 。
关于 三体, 我在 《一体方程 二体方程 三体方程》 https://www.cnblogs.com/KSongKing/p/12075154.html 中 提出了 “K 氏 n-体 猜想” 。
那, 接着, 我们可以问, 如果 积分路径 是 曲面 呢 ? 如何 来 求 曲面积分 的 最小条件 ? 或者说, 曲面 是 什么样 时, 在 曲面 上 的 某个 定积分 值 最小 ?
是不是 应该有个 三维版 的 欧拉-拉格朗日 方程 ? 或者 三维版 的 变分法 ? 或者说, 曲面版 的 欧拉-拉格朗日 方程, 曲面版 的 变分法 。
上文 提到 曲面 上 的 短程线 、最速降线, 还可以加一种线, 自由降线 。 将 一个 小球 放在 曲面 上, 让 它 在 重力作用 下 滚动, 小球 滚过 的 轨迹 就是 自由降线 。
曲面 上 的 短程线 、最速降线 、自由降线 合起来称为 “曲面上常见的三种线” 。
短程线 、最速降线 是 泛函问题, 自由降线 是 微分方程问题, 但是, 自由降线 太复杂了, 也可能变成 泛函问题, 来求 “最接近 理论解 的 那个路径” , 或者 “可能 的 若干 路径” 。
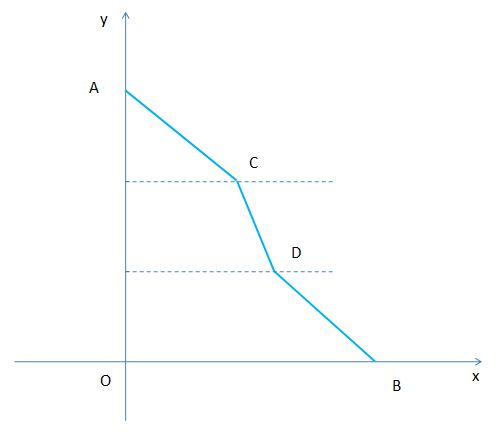
留一道题 :
如图, 光线 从 A 点 出发, 沿 AC 以 速度 v1 到达 C 点, 沿 CD 以 速度 v2 到达 D 点, 沿 DB 以 速度 v3 到达 B 点,
A 点坐标 是 ( 0, 3h ) , B 点 坐标 是 ( L, 0 ) , C 点 坐标 是 ( xc, 2h ) , D 点 坐标 是 ( xd, h ) , h 、L 为 常量 。
问 C 点 D 点 的 横坐标 xc 、xd 是 多少 时, 光 从 A 到 B 的 时间 最短 ?
参考资料 :
《最速降线的数学模型—变分法》 https://www.jianshu.com/p/961e890e88b2
《最速降线问题》 https://www.cnblogs.com/lfri/p/10327570.html
《路径积分一:构造路径积分》 https://zhuanlan.zhihu.com/p/25140463
《如何理解路径积分》 https://zhidao.baidu.com/question/1798621614932923107.html
《费马原理的原理?》 https://www.zhihu.com/question/44736014
《费马原理是基本的吗?》 https://www.zhihu.com/question/374743354
《光是如何知道哪条路线最快的,费马原理是不是违背常理呢?》 https://www.zhihu.com/question/20465361
《寻找“最好”(2)——欧拉-拉格朗日方程》 https://www.cnblogs.com/bigmonkey/p/9519387.html