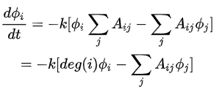先说问题的本质:图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。
要想理解GCN以及其后面一系列工作的实质,最重要的是理解其中的精髓Laplacian矩阵在干什么。知道了Laplacian矩阵在干什么后,剩下的只是解法的不同——所谓的Fourier变换只是将问题从空域变换到频域去解,所以也有直接在空域解的(例如GraphSage)。为了让问题简单便于理解,先让我们忘记时域、频域这些复杂的概念,从一个最简单的物理学现象——热传导出发。
图(Graph)上的热传播模型
众所周知,没有外接干预的情况下,热量从温度高传播到温度低的地方并且不可逆,根据著名的牛顿冷却定律(Newton Cool's Law),热量传递的速度正比于温度梯度,直观上也就是某个地方A温度高,另外一个B地方温度低,这两个地方接触,那么温度高的地方的热量会以正比于他们俩温度差的速度从A流向B。
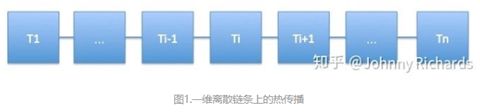
从一维空间开始
我们先建立一个一维的温度传播的模型,假设有一个均匀的铁棒,不同位置温度不一样,现在我们刻画这个铁棒上面温度的热传播随着时间变化的关系。预先说明一下,一个连续的铁棒的热传播模型需要列温度对时间和坐标的偏微分方程来解决,我们不想把问题搞这么复杂,我们把空间离散化,假设铁棒是一个一维链条,链条上每一个单元拥有一致的温度,温度在相邻的不同的单元之间传播,如下图:
对于第i 个单元,它只和 i-1 与 i+1 两个单元相邻,接受它们传来的热量(或者向它们传递热量,只是正负号的差异而已),假设它当前的温度为Φi,那么就有:
k和单元的比热容、质量有关是个常数。右边第一项是下一个单元向本单元的热量流入导致温度升高,第二项是本单元向上一个单元的热量流出导致温度降低。做一点微小的数学变换可以得到:
注意观察第二项,它是两个差分的差分,在离散空间中,相邻位置的差分推广到连续空间就是导数,那么差分的差分,就是二阶导数!
所以,我们可以反推出铁棒这样的连续一维空间的热传导方程就是:
同理,在高维的欧氏空间中,一阶导数就推广到梯度,二阶导数就是我们今天讨论的主角——拉普拉斯算子
其中 Δ 这个符号代表的是对各个坐标二阶导数的加和,现在的主流写法也可以写作 Δ2 。综上所述,我们发现这样几个事实:1、在欧氏空间中,某个点温度升高的速度正比于该点周围的温度分布,用拉普拉斯算子衡量。2、拉普拉斯算子,是二阶导数对高维空间的推广。那么,你肯定会问:你扯这么多有什么用呢?我还是看不到拉普拉斯算子和拉普拉斯矩阵还有GCN有半毛钱关系啊?不要急,目前只是第一步,让我们把这个热传导模型推广导拓扑空间,你就会发现它们其实刻画的是同一回事了!
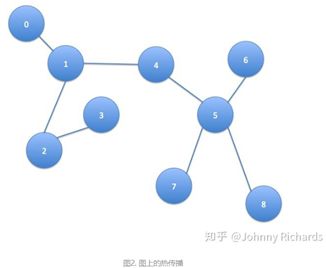
图(Graph)上热传播模型的推广
现在,我们依然考虑热传导模型,只是这个事情不发生在欧氏空间了,发生在一个Graph上面。这个图上的每个结点(Node)是一个单元,且这个单元只和与这个结点相连的单元,也就是有边(Edge)连接的单元发生热交换。例如下图中,结点1只和结点0、2、4发生热交换,更远的例如结点5的热量要通过4间接的传播过来而没有直接热交换。
我们假设热量流动的速度依然满足牛顿冷却定律,研究任一结点,它的温度随着时间的变化可以用下式来刻画:
其中 A 是这个图的邻接矩阵(Adjacency Matrix),定义非常直观: 对于这个矩阵中的每一个元素 Aij ,如果结点 i 和 j 相邻,那么Aij =1 ,否则 Aij =0 。在这里,我们只讨论简单情况:
1、这张图是无向图,i 和 j 相邻那么 j 和 i 也相邻,所以 Aij = Aji 这是个对称阵。
2、结点自己到自己没有回环边,也就是 A 对角线上元素都是 0 。
所以不难理解上面这个公式恰好表示了只有相邻的边才能和本结点发生热交换且热量输入(输出)正比于温度差。我们不妨用乘法分配律稍微对上式做一个推导:
先看右边括号里面第一项, deg( ) 代表对这个顶点求度(degree),一个顶点的度被定义为这个顶点有多少条边连接出去,很显然,根据邻接矩阵的定义,第一项的求和正是在计算顶点 i 的度。
再看右边括号里面的第二项,这可以认为是邻接矩阵的第i 行对所有顶点的温度组成的向量做了个内积。
为什么要作上述变化呢,我们只看一个点的温度不太好看出来,我们把所有点的温度写成向量形式再描述上述关系就一目了然了。首先可以写成这样:
然后我们定义向量:
![]()
那么就有:
![]()
D被称为度矩阵,只有对角线上有值,且这个值表示对应的顶点度的大小。整理整理,我们得到:
回顾刚才在连续欧氏空间的那个微分方程:
二者具有一样的形式!我们来对比一下二者之间的关系:
- 相同点:刻画空间温度分布随时间的变化,且这个变化满足一个相同形式的微分方程。
- 不同点:前者刻画拓扑空间有限结点,用向量 Φ 来刻画当前状态,单位时间状态的变化正比于线性变换 -L 算子作用在状态 Φ 上。后者刻画欧氏空间的连续分布,用函数 Φ(x, t) 来刻画当前状态,单位时间状态变化正比于拉普拉斯算子 Δ 作用在状态 Φ上。
不难发现,这就是同一种变换、同一种关系在不同空间上面的体现,实质上是一回事!
于是我们自然而然,可以把连续空间中的热传导,推广到图(Graph)上面去,我们把图上面和欧氏空间地位相同变换,以矩阵形式体现的 L 叫做拉普拉斯(Laplacian)矩阵。看,这正是 @superbrother 答案中所述的原始形式的拉普拉斯矩阵 L=D-A 。
需要多嘴一句的是,本文开头所说的离散链条上的热传导,如果你把链条看成一个图,结点从左到右编号1,2,3...的话,也可以用图的热传导方程刻画,此时 除了头尾两个结点是1其他值都是2, 的主对角线上下两条线上值是1,其他地方是0。
推广到GCN
现在问题已经很明朗了,只要你给定了一个空间,给定了空间中存在一种东西可以在这个空间上流动,两邻点之间流动的强度正比于它们之间的状态差异,那么何止是热量可以在这个空间流动,任何东西都可以!
自然而然,假设在图中各个结点流动的东西不是热量,而是特征(Feature),而是消息(Message),那么问题自然而然就被推广到了GCN。所以GCN的实质是什么,是在一张Graph Network中特征(Feature)和消息(Message)中的流动和传播!这个传播最原始的形态就是状态的变化正比于相应空间(这里是Graph空间)拉普拉斯算子作用在当前的状态。
抓住了这个实质,剩下的问题就是怎么去更加好的建模和解决这个问题。
建模方面就衍生出了各种不同的算法,你可以在这个问题上面复杂化这个模型,不一定要遵从牛顿冷却定律,你可以引入核函数、引入神经网络等方法把模型建得更非线性更能刻画复杂关系。
解决方面,因为很多问题在频域解决更加好算,你可以通过Fourier变换把空域问题转化为频域问题,解完了再变换回来,于是便有了所有Fourier变换中的那些故事。
扯了这么多,总结一下,问题的本质就是:
- 我们有张图,图上每个结点刻画一个实体,物理学场景下这个实体是某个有温度的单元,它的状态是温度,广告和推荐的场景下这个实体是一个user,一个item,一个ad,它的状态是一个embedding的向量。
- 相邻的结点具有比不相邻结点更密切的关系,物理学场景下,这个关系是空间上的临近、接触,广告和推荐场景下这个是一种逻辑上的关系,例如用户购买、点击item,item挂载ad。
- 结点可以传播热量/消息到邻居,使得相邻的结点在温度/特征上面更接近。
本质上,这是一种Message Passing,是一种Induction,卷积、傅立叶都是表象和解法。
最后再补充说明几点事实:
热/消息传导方程的数值可迭代求解性(机器学习上的可操作性)
我们可以把原方程写成这样:
机器学习中,时间是离散的,也就是左边对时间的求导变成了离散的一步步迭代。好在这个方程天生似乎就是上帝为了我们能够迭代求解而设计的。右边用拉普拉斯算子作用一次到全局的状态上,就能把状态更新一步!
实际解决的过程中,可以发挥机器学习搬砖工懂得举一反三的优良精神,首先,不一定要全局操作,我们可以batchify操作一部分结点,大家轮着来,其次,我们可以只考察这个点的一阶和二阶邻居对当前点作Message Passing,这个思想就是对拉普拉斯算子作特征分解,然后只取低阶的向量,因为矩阵的谱上面能量一般具有长尾效应,头几个特征值dominate几乎所有能量。
Laplacian算子的另一个性质
Laplacian矩阵/算子不仅表现的是一种二阶导数的运算,另一方面,它表现了一种加和性,这个从图上热/消息传播方程最原始的形态就能一目了然:
可见,每个结点每个时刻的状态变化,就是所有邻居对本结点差异的总和,也就是所有的邻居把message pass过来,然后再Aggregate一下,这正是GraphSage等空域算法的关键步骤Aggregate思想的滥觞。
在实际建模中,我们的Aggregate不一定是加和,作为一个熟练的机器学习搬砖工,我们懂得可以把Aggregate推广成各种操作例如Sum Pooling,例如LSTM,例如Attention,以求刷效果,发paper :)
两种空间下的Fourier分解/ 特征分解对比(卷积为什么能从欧氏空间推广到Graph空间)
最后,因为有以上分析作基础,我们可以解释一下傅立叶变换是怎么推广到图空间的。
https://en.wikipedia.org/wiki/Laplacian_matrix