本单元围绕表达式求导展开,由浅入深,由易到难,令人收获良多。通过这一单元的练习,我不仅掌握了一定的Java知识,更重要的是摆脱了固有的面向过程思维定式,逐渐认识了面向对象的思想。
一、基于度量分析程序结构(使用MetricsReloaded插件)
1.1 第一次作业
设计思路:由于第一次作业较容易,也没能理解出题意图,只当做一个用来熟悉java语言的编程作业。如果只包含x的幂函数,那么可以只建立一个Polynomial类,类成员包括系数的ArrayList, 指数的ArrayList以及项数termnum。幂函数的求导实现很简单,难点在于提取各项以及如何优化输出。
1.1.1 类图
只有一个类,包含了对输入字符串的预处理、处理、求导、合并同类项以及输出等方法,事实上是一种面向过程的方式。
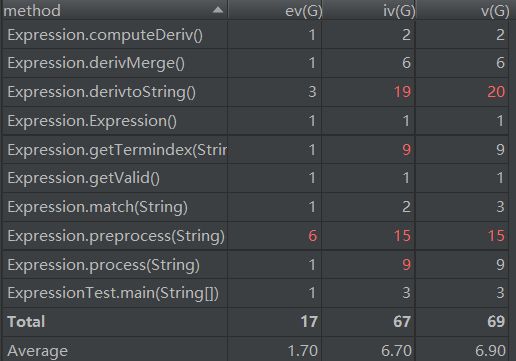
1.1.2 复杂度分析
java代码行数只有215行。
在方法复杂度上,ev(G)为基本复杂度,用来衡量程序非结构化程度。基本复杂度越高意味着非结构化程度越高,难以模块化和维护。iv(G)为设计复杂度,即模块与模块的调用关系。软件模块设计复杂度高意味着模块耦合度高,导致模块难以维护、隔离和复用。v(G)为圈复杂度,衡量一个模块判定结构的复杂程度,程序的可能错误和高的圈复杂度有很大关系。(参考博客:https://kb.cnblogs.com/page/573406/)
1.1.3 优缺点分析
如果硬要说优点的话,那么优点在于思路很简单,大部分是体力活。但缺点是显而易见的,代码复用性很低,并且方法之间调用频繁。应抽象出项这一个层次,这样代码会更好维护和进行复用。
1.2 第二次作业
设计思路:本次作业在前一次作业上增加了sin(x)和cos(x)因子。每一项的系数、x的次数、sin(x)的次数、cos(x)的次数可用四元组表示(a,b,c,d),根据函数求导法则,可以得到三个四元组。在第一次作业的基础上,增加sin(x)和cos(x)的指数作为类成员,然后修改表达式的提取和输出即可。
1.2.1 类图
还是只有一个Expression主类,由于与第一次思路类似,类成员与类方法也相似。
1.2.2 复杂度分析
由于思路与第一次作业类似,加上多了sin(x)和cos(x)的因子,在字符串的预处理、处理以及输出上的复杂度仍较高。
1.2.3 优缺点分析
同第一次作业一样,都属于思路简单实现费劲的类型。虽然与第一次作业的思路类似,但是在原来的代码上进行改动已经很难实现(容易出错),于是我干脆对着第一次的代码重新写了一遍。缺点是复杂度搞高,复用性差,在面对第三次作业时直接推倒重来。优点体现在优化的实现上,由于四元组的表示方法,优化时可以直接对系数进行比较操作。
1.3 第三次作业
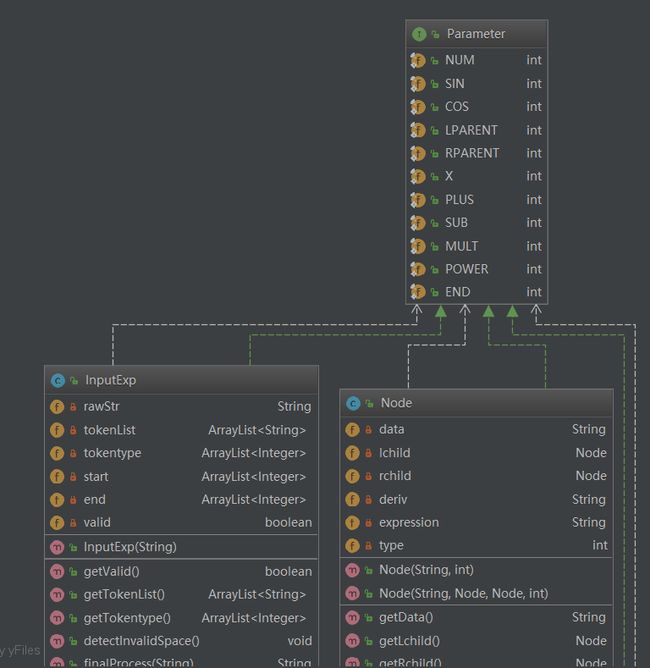
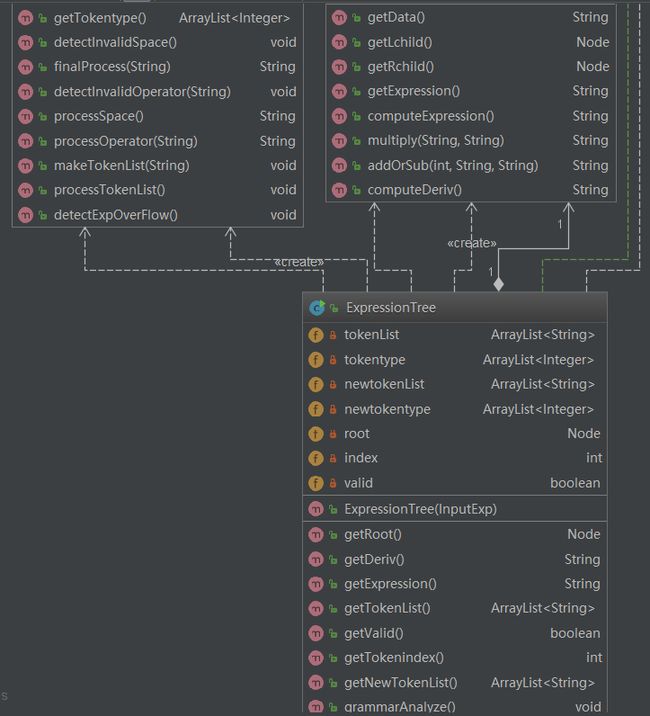
设计思路:第三次作业加入了嵌套因子和表达式因子,使得前两次作业的代码对第三次没有任何意义。于是本次作业我设计了三个类,表达式提取类,表达式树类和节点类,以及一个存储参数的接口。主要思路是根据提取后的表达式构建一棵表达式树,并在树上进行求导运算。
1.3.1 类图
共有三个类以及一个接口。
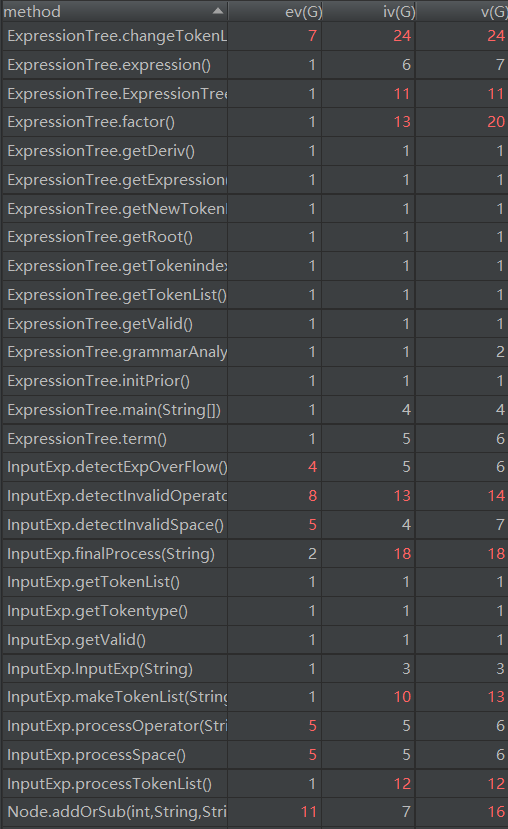
1.3.2 复杂度分析
相比于前两次作业,复杂度有了一定的降低,这与抽象层次的增加有关系。而大多数复杂度较高的方法,都是在字符串处理上。由于本次直接大正则行不通,因此我采用了编译技术中的词法分析技术和递归向下的语法分析技术进行分析。这在一定程度上提高了复杂度,如Expression类中的factor()方法,因控制语句过多而使得复杂度较高。
类间依赖复杂度并不高。
1.3.3 优缺点分析
本次作业的优点在于:建立起了表达式树-节点的抽象层次,并且专门建立了InputExp对输入表达式的字符串进行处理。因此,代码更容易维护,复用性强。如果增加新的需求,仍然可以通过这样的抽象层次来实现。
缺点:在节点的处理上,由于划分得还是不够仔细,使得在计算节点代表的表达式以及导数时,仍需要较多的控制分支,增加了代码的复杂度,容易出错并且难以定位。字符串的处理依旧显得繁琐。此外,根据节点求出表达式后,表达式的优化十分困难。
二、分析程序bug
2.1 出现的bug如下:
(1)数据范围。如第一次作业时,我并未在意指导书中强调的数据类型问题,为了方便只使用了long这一基本数据类型,加之中测没有相应样例以及自己没有意识(还是太naive),强测涉及数据范围的考察点直接雪崩。出现在表达式类的成员定义中。
(2)ArrayList误操作的bug。在进行合并同类项时,对ArrayList会有remove操作,但一次remove后所有元素向前移动,因此在遍历时若不注意下标,则会出现漏项。出现在表达式提取中。
(3)正则表达式匹配。在作业中,若使用正则表达式默认的贪婪模式,则在表达式过长时,会由于回溯出现爆栈。将正则表达式改为独占模式进行匹配即可。出现在表达式提取中。
(4)判断WRONG FORMAT时情况的遗漏。尤其是第三次作业,不能直接使用大正则来匹配,需要自己检测非法空格和非法的加减号。若考虑不周全,则会出现误判的情况。出现在表达式的预处理中。
(5)表达式字符串的处理。在对输入的表达式字符串处理时,为了统一各项,在表达式的第一项,若有加号或者减号,则在其之前添加0。我在第三次作业处理时,只考虑了表达式因子的情况,即'('后跟‘+’的情况,遗漏了整个表达式的第一项,导致后面使用pop()时抛出了异常。出现在表达式处理中。
(6)sin和cos中包含复合因子的情况。按照常识sin(2*x)是合法的,但在指导书中是非法的,因为2*x作为表达式因子需要加括号。而我在节点上返回乘法时,是没有加括号的,这应该是作业三中一个未公开的弱测样例。这个bug出现在树上node的求表达式计算中。
(7)还有一个不算bug的隐患。由于我的表达式优化效果较差,输出的结果含有较多的括号未化简。由于指导书规定了输入表达式长度不多于60,不存在问题。若指导书放宽输入的限制,则有可能构造一个极端的测试样例,使得括号嵌套层数超过MATLAB的限制。这是优化层面的问题。
(8)equals方法和==的疏忽。由于习惯性地使用==,导致在进行对象比较原本应使用equals()时使用了==,从而出错。这样的错误在debug时还很难发现。
2.2 bug位置与设计结构的关系
由以上bug可以发现,在表达式字符串的处理上存在着诸多问题。尤其是在判断非法的符号、空格以及加减号上,采用了诸多控制分支和循环遍历来判断,这就导致程序结构会显得较乱。而在这种结构不清晰,情况靠枚举的位置,就是程序bug最容易出现的位置。相对而言,在设计思路清晰,结构清晰的程序段,出错的概率就要小很多。
2.3 从分类树角度分析程序在设计上的问题
分类树方法是将测试对象的可能输入按照不同的方式进行分类,将各种分开的输入组合到一起产生不冗余的测试用例,同时又能覆盖测试对象的整个输入域。
在程序的设计上,可能就存在一些没有考虑到的情况,例如+++ 1、(+ + 1)这样的错误样例,以及sin(2*x)这种符合常识但不符合指导书要求的样例。根据指导书提供的基础样例以及自己设计的样例进行组合,才发现设计上的漏洞,从而进行弥补。
三、发现bug的策略
由于高工课程没有互测这一环节,因此在这里只谈我对自己的代码是如何发现bug的。
首先列出自己对各种情况的考量思路,首要排除思路上出现的遗漏。例如非法的空格包括哪些情况,非法的加减号包括哪些情况等。
其次设计测试样例,尤其是根据代码设计结构来设计测试用例,也就是白盒测试。在设计样例时,将代码的逻辑分支全部覆盖。例如在检测非法空格时操作符时,按照加号的个数分类,1、2、3、大于3。使得每个类别均能接受到测试。此外,在对+号开头的表达式进行测试时,也是按照这一策略进行。在这样的策略下,发现了不少分支下都存在着==的误用以及下标误用等错误。
四、Applying Creational Pattern
在创建模式的应用上,第三次作业有很大的提升空间。
从现有的架构来看,在Node类中,仍有较多的情况用if else表示,这增加了代码的复杂度,也使得代码的可读性差。可以建立一个工厂类,根据运算的不同种类创建不同的Node,不同类型的Node各自只处理一种符号的求导和计算表达式。这样会大大降低Node类的复杂度和维护的难度。
五、总结
总而言之,通过第一单元的学习,虽然直到第三次作业仍有许多不足,例如抽象层次不够细化、类方法的复杂度较高等问题,但我已经逐步意识到面向对象的重要性并取得了一定的进步,也算是入门OO了。希望在今后接触更多的设计模式,真正实现OO吧。