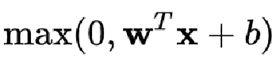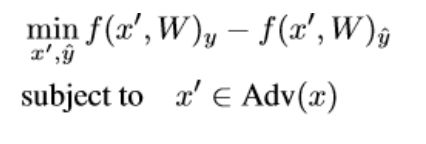鲁棒性验证-第五小组

《TRAINING FOR FASTER ADVERSARIAL ROBUSTNESS VERIFICATION VIA INDUCING RELU STABILITY》论文分享报告

组员：杨根 黎君玉 张荣华

1 基础知识

ReLU函数

线性整流函数（Rectified Linear Unit, ReLU），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。ReLU函数函数图像如下所示。

对于进入神经元的来自上一层神经网络的输入向量 {\displaystyle x} x，使用线性整流激活函数的神经元会输出

 

 

至下一层神经元或作为整个神经网络的输出（取决现神经元在网络结构中所处位置。

 

 

 

sign（x）函数

sign（x），这是一个符号函数，用于把函数的符号析离出来，在数学和计算机运算中，其功能是取某个数的符号（正或负）：

当x>0，sign(x)=1;

当x=0，sign(x)=0;

当x<0， sign(x)=-1；

在通信中，sign(t)表示这样一种信号：

当t≥0，sign(t)=1; 即从t=0时刻开始，信号的幅度均为1；

当t<0， sign(t)=-1；在t=0时刻之前，信号幅度均为-1

2问题描述

机器学习模型做出的预测通常很脆弱。容易受到对抗攻击。验证对所有攻击是否都具有强大的抵抗力，验证过程的速度很慢。

3 解决方案

目标：训练不仅对对抗性扰动具有鲁棒性的神经网络，而且可以更容易地验证其鲁棒性。

在这项工作中，作者使用协同设计的原理来开发训练技术，从而使模型既健壮又易于验证。作者的技术依赖于改善网络的两个关键属性：稀疏性和ReLU稳定性。具体来说，首先表明，在训练过程中提高体重平衡的自然方法（如“ 1-正则化”）可以比目前的方法更快地得到验证。之所以会加快速度，是因为通常来说，精确的验证者受益于验证任务表述中变量的减少。例如，对于依赖线性编程（LP）求解器的精确验证器，稀疏权重矩阵意味着这些约束中的变量较少。然后，关注于ReLU网络精确验证的当前方法的主要速度瓶颈：需要精确验证方法来“分支”，考虑每个ReLU的两种可能情况（ReLU是活动的还是不活动的）。分支急剧增加了验证的复杂性。因此，如果优化后的验证者可以确定ReLU是稳定的，即对于输入的任何扰动，ReLU将始终处于活动状态或始终处于非活动状态，则无需在ReLU上进行分支。这激发了本文提出的技术的关键目标：作者旨在通过最大化稳定ReLU的数量来最大程度地减少分支。将此目标称为ReLU稳定性，并引入一种正则化技术来诱导它。能够为MNIST和CIFAR10训练重量稀疏和ReLU稳定的网络，这些网络可以被更快地验证。具体来说，通过将诱发体重减轻的自然方法与强大的对抗训练程序结合起来（参见Goodfellow等人（2015）），作者能够训练网络，在这段时间内可以验证近90％的输入与以前的验证技术相比，它很小。然后，通过添加用于诱导ReLU稳定性的正则化技术，作者可以训练模型，使其能够被验证额外快4到13倍，同时又能保持MNIST的最新准确性。作者的技术对CIFAR模型的精确验证显示出类似的改进。特别是，对于∞范数约束的对手，作者实现了以下验证速度和可证明的鲁棒性结果：

 

 

 

4相关设计

三种训练可验证的网络模型：

验证网络：

改善网络的两个关键属性：稀疏性和ReLU稳定性。

稀疏性：自然正则化方法

ReLU稳定性：一种新的正则化方法

对于输入的任何扰动，ReLU将始终处于活动状态或始终处于非活动状态，则无需在ReLU上进行分支。

旨在通过最大化稳定ReLU的数量来最大程度地减少分支。

4.1验证网络模型的鲁棒性

   具有ReLU非线性的k层全连接前馈DNN分类器4。可以将此类模型视为函数f（·，W，b），其中W和b代表每层的权重矩阵和偏差。对于输入x，DNN的输出f（x，W，b）定义为：

 

 

 

应用于其他p范数和更广泛的扰动集。验证网络模型。对于带有正确标签y的输入x，如果输入x0使某个不正确标签y的对数大于x0上的y的对数，则会造成分类错误。因此，我们可以将寻找对抗性扰动的任务表示为优化问题：

 

 

 

 

4.2重量稀疏性及其对验证速度的影响

两种自然的正则化方法：

l1-正则化和小权重修剪

 

 

 

4.3稳定性

验证者面对的情况越多，必须考虑的分支就越多，从而导致验证的复杂性呈指数增长。直观地讲，具有1000个ReLU的模型比仅有200个都需要分支的ReLU的模型更容易验证。因此，如果在具有允许扰动集Adv（x）的输入x上ReLU的数量使得被最大化。

 

 

 

计算出的上限和下限

如果，则可以分别用身份函数或零函数替换ReLU。

如果，则这些验证者确定他们需要对该ReLU“分支”。

这里就是ReLU修剪

 

 

 

一个确切表示ReLU何时稳定的函数

 

 

 

不可微，近似：

 

 

 

 

 

 

Relu稳定性改进对可证明的对抗精度的影响

 

 

 

 

5实验环境

在表3中。作者比较了它们的测试集准确性，PGD对抗性准确性（针对强大的40步PGD对抗性攻击的鲁棒性评估）和可证明的对抗性准确性。此外，为了表明作者的方法可以扩展到更大的体系结构，作者针对每个数据集和训练并验证了“ + RS（大）”网络。在MNIST上可证明的对抗性泌尿激素的中间结果，比Wong等人的结果明显要好。 （2018）对于较大的扰动= 0.3，并且可比较的= 0.1。在CIFAR10上，作者的方法不太有效，这也许表明，要使纯鲁棒的CIFAR分类器更稳定，必须使用更不稳定的ReLU。作者还遇到了许多实例，它们在CIFAR上达到了分配的120秒时间限制，尤其是对于ReLU稳定性较差的控制网络。

 

6优缺点分析

1. 使用协同设计的原理来开发强调验证为目标的训练方法，并且表明它们可以更快地验证训练后的模型。
2. 证明自然正则化方法可以使确切的验证问题变得更加易于处理。
3. 提出了一种改善网络ReLU稳定性的方法，并表明这种改进使验证速度提高了4到13倍。
4. 改善稳定性方法是通用的，它可以添加到任何训练过程中，并且可以加快任何精确的验证过程。