《数据结构与算法分析——C语言描述》ADT实现(NO.04) : AVL树（AVL-Tree）

上次我们已经实现了普通的二叉查找树。利用二叉查找树，可以用O(logN)高度的树状结构存储和查找数据，提高了存储和查找的效率。

然而，考虑一种极端情形：依次插入1,2,3,4,5,6,7,8,9九个元素，形成的二叉查找树实际上是一个线性表，每层只有一个元素，元素数与层数相同。

事实上，不只这一种情形。在很多情况下，都有可能出现这种结构。这样一来，二叉查找树就失去了它存在的意义。于是，我们考虑在每次插入和删除元素时，对树的结构进行一些检查和维护，使其每层的元素数尽可能多，从而尽可能降低层数，我们称为平衡。

AVL树即是对二叉查找树的一种平衡方法。其要求为，每个结点的左右子树高度差不超过1.

于是，我们需要在结点的结构中增加一个height成员，每次插入或删除时，更新这个成员，并检测是否满足上述条件，若不满足，则需调整树的结构。

不难想到，如果每次违背上述条件时，都及时进行调整，那么违背条件的情况一定是左右子树高度差为2的情况。所以，对左右子树高度差为2这种特殊情形进行分析。

我们可以将这种情况进行分类，分为（简记）：左左，左右，右左，右右四种。

以第一种情况为例，形象地说，左左即左子树比右子树高度大2，且左子树偏向左侧。如果用二叉树的属性来描述，即左子树的左子树高度大于右子树高度。

其他三种情况类似，不再赘述。

由对称性，左左和右右实际为一种情况，左右和右左为另一种情况。所以，算法的设计，只需要考虑这两种情况。具体代码则需要分四种情况来实现。

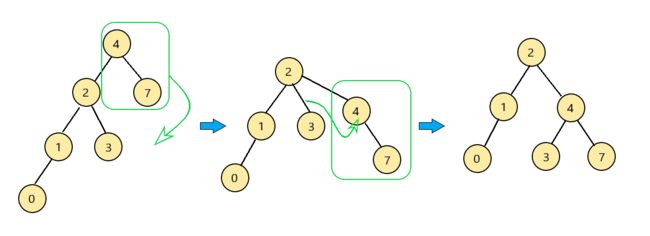
对于左左，我们采取单旋转（Single Rotate）的方法来进行调整。如图：

而对于左右，我们采取双旋转（Double Rotate），即两次单旋转的方法来调整：先对左子树进行右侧单旋转（即上述图示旋转方向的反方向），再对原结点进行左侧单旋转。这里不再说明这种方法为何正确。

代码如下：

// AvlTree.h

#include 
#include 

struct _AvlNode;
typedef struct _AvlNode AvlNode;
typedef AvlNode *Position;
typedef AvlNode *AvlTree;

AvlTree MakeEmpty(AvlTree T);
Position Find(ElementType X, AvlTree T);
Position FindMin(AvlTree T);
Position FindMax(AvlTree T);
AvlTree Insert(ElementType X, AvlTree T);
AvlTree Delete(ElementType X, AvlTree T);
ElementType Retrieve(Position P);

　　

// AvlTree.c

#include "AvlTree.h"

struct _AvlNode
{
    ElementType Element;
    AvlTree Left;
    AvlTree Right;
    int Height;
};

int Height(AvlTree T)
{
    return T ? T->Height : 0;
}

AvlTree MakeEmpty(AvlTree T)
{
    if (T != NULL)
    {
        MakeEmpty(T->Left);
        MakeEmpty(T->Right);
        free(T);
    }
    return NULL;
}

Position Find(ElementType X, AvlTree T)
{
    if (T == NULL)
        return NULL;
    else if (T->Element < X)
        return Find(X, T->Right);
    else if (T->Element > X)
        return Find(X, T->Left);
    else
        return T;
}

Position FindMin(AvlTree T)
{
    if (T != NULL)
        while (T->Left != NULL)
            T = T->Left;
    return T;
}

Position FindMax(AvlTree T)
{
    if (T != NULL)
        while (T->Right != NULL)
            T = T->Right;
    return T;
}

AvlTree SingleRotateWithLeft(AvlTree T)
{
    AvlTree temp;
    temp = T->Left;
    T->Left = temp->Right;
    temp->Right = T;
    temp->Height = Height(temp->Left) > Height(temp->Right) ? Height(temp->Left) + 1 : Height(temp->Right) + 1;
    T->Height = Height(T->Left) > Height(T->Right) ? Height(T->Left) + 1 : Height(T->Right) + 1;
    return temp;
}

AvlTree SingleRotateWithRight(AvlTree T)
{
    AvlTree temp;
    temp = T->Right;
    T->Right = temp->Left;
    temp->Left = T;
    temp->Height = Height(temp->Right) > Height(temp->Left) ? Height(temp->Right) + 1 : Height(temp->Left) + 1;
    T->Height = Height(T->Right) > Height(T->Left) ? Height(T->Right) + 1 : Height(T->Left) + 1;
    return temp;
}

AvlTree DoubleRotateWithLeft(AvlTree T)
{
    T->Left = SingleRotateWithRight(T->Left);
    return SingleRotateWithLeft(T);
}

AvlTree DoubleRotateWithRight(AvlTree T)
{
    T->Right = SingleRotateWithLeft(T->Right);
    return SingleRotateWithRight(T);
}

AvlTree Insert(ElementType X, AvlTree T)
{
    if (T == NULL)
    {
        if ((T = (AvlTree)malloc(sizeof(AvlNode))) == NULL)
        {
            printf("Error! Out of space! \n");
            return NULL;
        }
        else
        {
            T->Element = X;
            T->Left = T->Right = NULL;
            T->Height = 0;
        }
    }
    else if (X < T->Element)
    {
        T->Left = Insert(X, T->Left);
        if (Height(T->Left) - Height(T->Right) == 2)
        {
            if (X < T->Left->Element)
                T = SingleRotateWithLeft(T);
            else
                T = DoubleRotateWithLeft(T);
        }
    }
    else if (X > T->Element)
    {
        T->Right = Insert(X, T->Right);
        if (Height(T->Right) - Height(T->Left) == 2)
        {
            if (X < T->Right->Element)
                T = DoubleRotateWithRight(T);
            else
                T = SingleRotateWithRight(T);
        }
    }
    T->Height = Height(T->Left) > Height(T->Right) ? Height(T->Left) + 1 : Height(T->Right) + 1;
    return T;
}

AvlTree Delete(ElementType X, AvlTree T)
{
    Position temp;
    if (T == NULL)
    {
        printf("Error! No such node! \n");
        return NULL;
    }
    if (X < T->Element)
    {
        T->Left = Delete(X, T->Left);
        T->Height = Height(T->Left) > Height(T->Right) ? Height(T->Left) + 1 : Height(T->Right) + 1;
        if (Height(T->Right) - Height(T->Left) == 2)
        {
            if (Height(T->Right->Left) > Height(T->Right->Right))
                T = DoubleRotateWithRight(T);
            else
                T = SingleRotateWithRight(T);
        }
    }
    else if (X > T->Element)
    {
        T->Right = Delete(X, T->Right);
        T->Height = Height(T->Left) > Height(T->Right) ? Height(T->Left) + 1 : Height(T->Right) + 1;
        if (Height(T->Left) - Height(T->Right) == 2)
        {
            if (Height(T->Left->Left) < Height(T->Left->Right))
                T = DoubleRotateWithLeft(T);
            else
                T = SingleRotateWithLeft(T);
        }
    }
    else
    {
        if (T->Left && T->Right)
        {
            temp = FindMin(T->Right);
            T->Element = temp->Element;
            T->Right = Delete(T->Element, T->Right);
        }
        else
        {
            temp = T;
            if(T->Left == NULL)
                T = T->Right;
            else if (T->Right == NULL)
                T = T->Left;
            free(temp);
        }
    }
    return T;
}

ElementType Retrieve(Position P)
{
    return P->Element;
}

　　

转载于:https://www.cnblogs.com/DrChuan/p/11335722.html