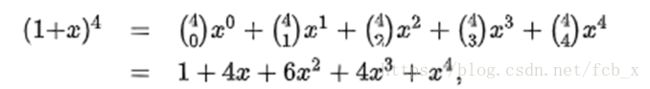组合数学 容斥原理 学习笔记 （福利向）和Leo一起做爱数学的好孩子（未完待续...

算法竞赛考得很多的部分啊

这个还是很重要的

在目前的算法竞赛中有三大计数考点

1）组合计数

2）线性计数

3）群论计数

其中群论计数比较困难，我又不知道什么是线性计数，所以只能颓组合计数。

首先是最简单的东西

加法原理

若完成一件事的方法有$n$类，其中第$i$类方法包含$ai$种不同的方法， 且这些方法互不重合，则完成这件事共有$a1+a2+...+an$种不同的方法

乘法原理

若完成一件事需要$n$个步骤，其中第$i$个步骤包含$ai$种不同的方法， 且这些步骤互不干扰，则完成这件事共有$a1\cdot a2\cdot ...\cdot an$种不同的方法

这些是稍有常识的OI小学生都会的东西

接着是组合数和排列数

组合数

In mathematics, a combination is a selection of items from a collection, such that (unlike permutations) the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a $k$-combination of a set $S$ is a subset of $k$ distinct elements of $S$. If the set has n elements, the number of $k$-combinations is equal to the binomial coefficient

(nk)=n(n−1)⋯(n−k+1)k(k−1)⋯1,(nk)=n(n−1)⋯(n−k+1)k(k−1)⋯1{\displaystyle {\binom {n}{k}}={\frac {n(n-1)\dotsb (n-k+1)}{k(k-1)\dotsb 1}},} {\binom {n}{k}}={\frac {n(n-1)\dotsb (n-k+1)}{k(k-1)\dotsb 1}}(kn​)=k(k−1)⋯1n(n−1)⋯(n−k+1)​,(kn​)=k(k−1)⋯1n(n−1)⋯(n−k+1)​
摘自wiki

https://en.wikipedia.org/wiki/Combination

从$n$个不同元素中取出$m$个组成一个集合（不考虑顺序），产生的
不同的集合数量为$C(n,m)=n!/(m!\cdot (n-m)!)$

这个存在是一个二项式系数的东西

观察上式可知展开是存在一个规律的这实际上也是高考知识点

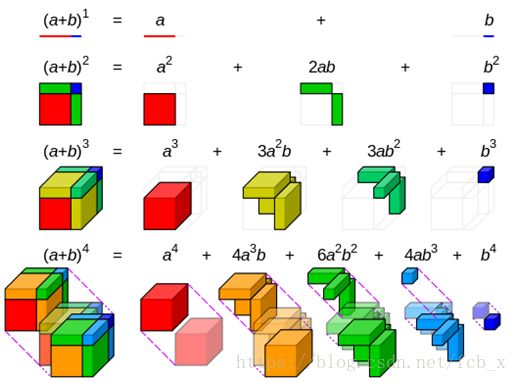
总结一下

这是二项式的一个简单形式（实际上还有牛顿的二项式定理）

这个时候伟大的数学家杨辉和帕斯卡先生先后独立发现了一个神奇的三角形

这个三角形有几个好性质

1）每一个数都是由左上角和右上角加在一起
2）一列加在一起等于右下角的值（以后讲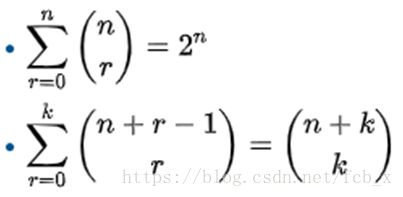

第一个式子可以配凑
第二个式子就是性质二（实际上是把$n+k$个里选$k$个给拆开选

组合数计算

这实际上很复杂，而且他很难直接算数理解，主要还是数形结合
------暂时咕掉------

容斥原理

Venn diagram showing the union of sets $A$ and $B$ as everything not in white
In combinatorics (combinatorial mathematics), the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

$|A\cup B|=|A|+|B|-|A\cap B|,|A\cup B|=|A|+|B|-|A\cap B|$,
where $A$ and $B$ are two finite sets and |S| indicates the cardinality of a set $S$ (which may be considered as the number of elements of the set, if the set is finite). The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection.

The principle is more clearly seen in the case of three sets, which for the sets $A$,$B$ and $C$ is given by

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|.|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|.$
This formula can be verified by counting how many times each region in the Venn diagram figure is included in the right-hand side of the formula. In this case, when removing the contributions of over-counted elements, the number of elements in the mutual intersection of the three sets has been subtracted too often, so must be added back in to get the correct total.

https://en.wikipedia.org/wiki/Inclusion–exclusion_principle

容斥原理是一种重要的组合数学方法，可以让你求解任意大小的集合，或者计算复合事件的概率。

在我看来维恩图是最好理解这个

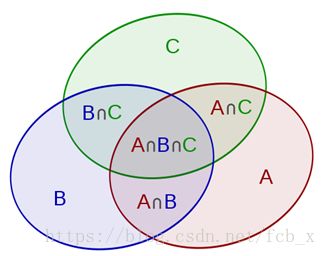
实际上我们容斥的目的是求这个的交集，我们的本质是算去重复的值。
换成数学上的语言就是：


总结成公式就是：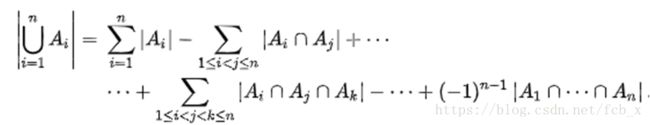

额这实际上是小学生都该会的，接下来你会见到各种各样的容斥系数求法。

额画个维恩图就会了。

容斥原理题目归类

这是本板块最激动人心的内容，也是博主呕心沥血之作

方程类

SDOI2013方程
HAOI2012容易题
这种题本质是求解一个无标号方程，由于有了上界所以需要容斥。

棋盘类

BZOJ4767
题解
怎样学习哲学
题解
BZOJ3782
题解
这一类题目的的大意实际上就是棋盘上有些干涉点不能走，问你走到某个点的走法总数。
这实际上是一种用DP把容斥降下来的方法。
大概套路是把干涉点排序然后O(N2)O(N^{2})O(N2)DP

区间满足要求的数类

CDOJ1544
题解
这个实际上就是最开始的那种做法，加上一个的倍数，减去两个的倍数之类的。
这道题稍有不同。
他的容斥系数要递推找规律。
这个模型还有隐藏在图上的题目。
COCI2009-2010 XOR
实际上还是一个道理的容斥
实际上满足要求的数模型还可以再分出一个模型：

区间满足近似要求的数类

SCOI2010幸运数字
题解
BZOJ2393
题解
这一类本质是爆搜，利用搜索的值增长率很快，直接剪枝

推出简单式子交换枚举顺序/变换类

CF998E
本题便是推出简单的容斥式子是O(N2)O(N^{2})O(N2)然后利用组合数意义递推变为$O(NlogN)$

披着反演外衣但实际本质可以容斥类

LOJ528
题解
DZY love Math 1
这一类题目本身是可以反演的。
但其本身含有mu函数，所以含有数学意义，可以容斥，而且普遍少个2倍常数。

容斥的值要构造

这是最普遍，最常见的容斥问题。

容斥的值需要DP

目前最毒的做过的是状压：
CQOI2012局部极小值
LGOJ1763
这个就是还要先状压。
还有普通DP的：
BZOJ3622
这道题是按照套路先算一个至少满足XXX的时候要DP

容斥的值套上别的计数问题

SHOI2016黑暗前的幻想乡
先上矩阵树，然后套路容斥。

容斥系数需要DP

UOJ390百鸽笼
比较神仙的题目，容斥系数在读进来以前是不知道的

容斥与二分图/DAG/连通图计数

毒瘤，主要相见FoolMike和他的COGS
HDU5713K个联通块
这种也算是套路容斥。
只是这道题最后还要跑个背包
BSOJ5051巨神兵
BZOJ3812
实际上这类题一般都是装压套容斥。
有一个lowbit技巧就是固定一个点再枚举。
如果你不满足COGS有很多这种题

转载于:https://www.cnblogs.com/Leo-JAM/p/10079088.html