回溯问题
上一讲 BruteForce算法的结尾中,我们提到了BruteForce算法的缺点,其中一条就是回溯问题,导致效率降低。
什么是回溯呢?
假设目标串S = "aaaaaaaab" T="aaab" 当我们利用BruteForce算法时,前三次的"aaa"的比较是毫无意义的,换言之,就是影响了效率。
KMP算法
为了提高效率,因此我们要使用KMP算法。KMP算法是一种改进后的算法,并且是由D.E.Knuth、V.R.Pratt和J.H.Morris同时发现的,因此称之为KMP算法。
其基本思想为:每当匹配过程中出现字符串比较不等时,不需要回溯指针,而是利用已经得到的“部分匹配”结果将整体模式向右“滑动”尽可能远的一段距离,继续进行比较。
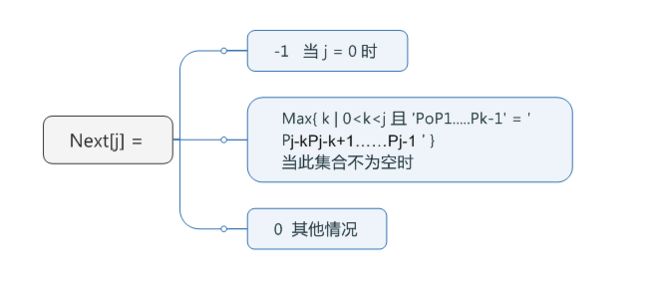
如何实现这个思想,换言之如何判断得到部分匹配结果?这里我们需要完成KMP算法中的第一步也是核心步骤:模式串求最大真子串。
1.模式串求最大真子串
举个栗子
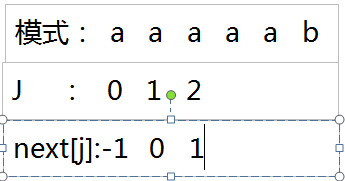
当J = 0 时 按照上面的思维导图公式,next[ j ] = -1
当 J = 1 时,next[ j ] = 0,因为我们想求模式串的最大真子串,而这个最大真子串是指不包含当前位置编号的字符,而是它前面的字符所构成的字符串里有没有最大真子串,因为 J = 1 时,模式串只有一个 a ,所以构不成最大真子串,因此属于其他情况,next[ j ] = 0
当 J = 2 时,next[ j ] = 1 ,因为当前位置编号的字符前面有2个 a,a 与 a 相等,满足我们的公式,并且他们的最大真子串长度为1(因为一个字符的长度为1),所以,记 next[ 2 ] = 1
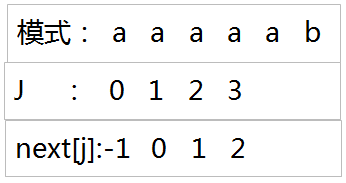
当 J = 3 时,next[ j ] = 2,因为同理,当前位置编号的字符前面有3个 a,第一个a与第二个a构成的字符串==第二个a与第三个a构成的字符串,长度为2,所以,记next[ 3 ] = 2
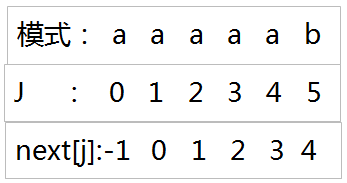
一次类推,最后的结果如图所示,不再赘述了。下图为另一个例子,大家可以对照答案看看有没有掌握好。
PS:当 J = 8 时 ,应比较前七个字符中是否有最大真子串,我们发现只有第一个a 和 第七个 a 满足公式,因此next[ 8 ] = 1
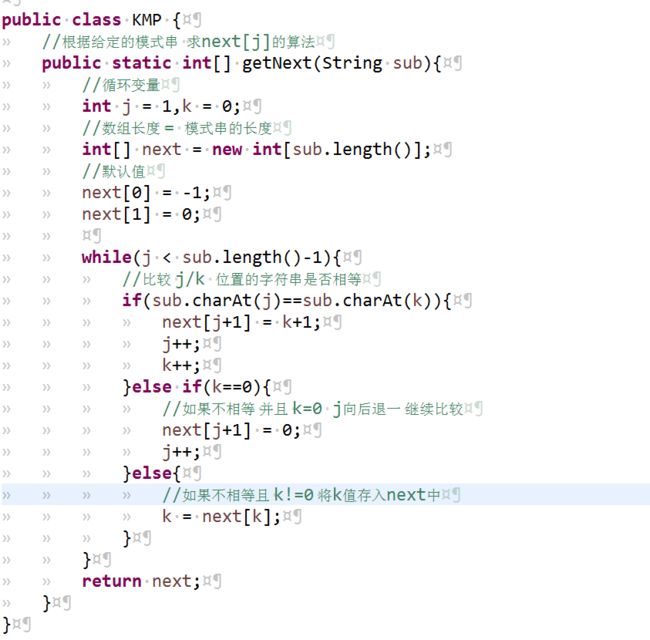
最大真子串的实现代码!
最大真子串的算法需要理解,同学们跟着代码的逻辑思路对照图表理解效果更佳。
2.KMP算法原理
KMP算法原理:当Si ≠ Tj, 若模式串存在最大真子串,可将模式串T按照 k=next[ j ] 的值向右滑动,然后比较 Si 和 Tk ,若仍有Si ≠ Tk,则模式串T按照新的 k=next[ j ] 的值向右滑动后比较。这样的过程一直进行到 k = next[ k ] = 0,此时若Si ≠ T0,则模式串T不再向右滑动,随后比较Si + 1 和 T0 。
原理很枯燥而且很难理解,但还是要写,显得很高大上 ^_^ 大家能不看就不看吧~
我们还是根据例子和图表来进行理解!
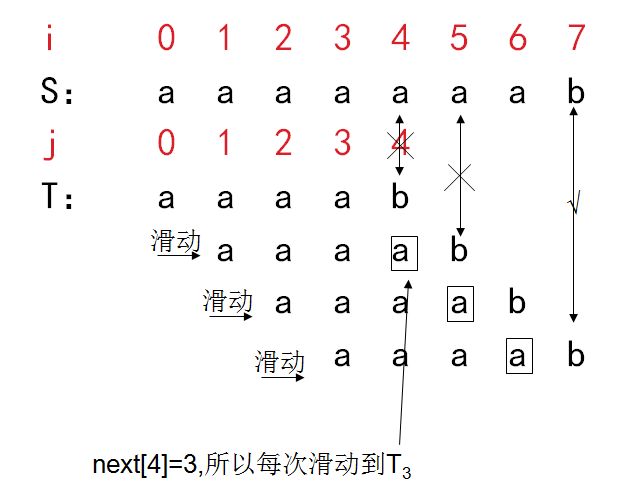
举个栗子 例如:主串 S = "aaaaaaab" 子串 = "aaaab" 采用KMP的模式匹配过程。
对应的最大真子串集如图。
首先一次进行比较,发现aaaa全部相等,当 b 时也就是J = 4时,由于不匹配,所以整体向右滑动一格,并且比较子串的第四个a,以此类推,最后完全匹配时,仅需要10次,大大提升了效率!!!
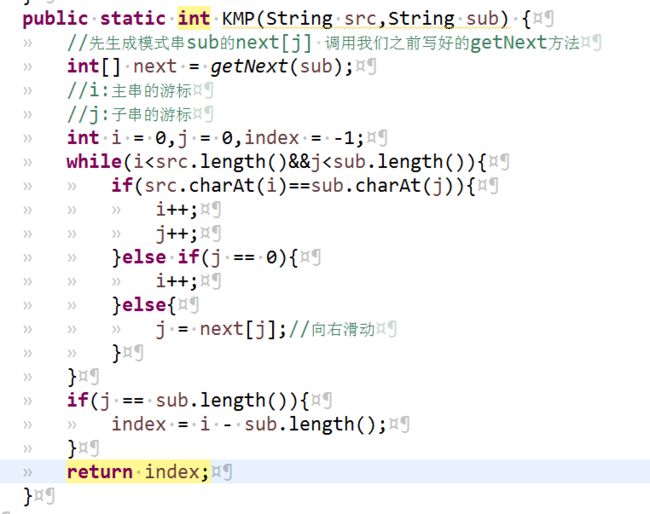
KMP实现代码!
两个方法都写在了KMP类里,同学们依然要跟着代码分析一遍,重点是对于最大真子串的理解。
大家可以写一个测试类,声明两个字符串,看一看匹配的输出结果~
输出结果为3哦!
KMP算法总结
KMP算法的效率是很高的,遇到相关算法题时也应该使用该算法进行解题,多多熟练也是好的嘛!
下一讲我们将会讲一个有意思的小游戏---彩票机选的算法与实现 期间用到的相关知识 我会整理在一节中 内容可能较多哦!
PS:有什么问题或者不解的地方可以评论,我都会一一就行回复的,如果有错误或者言语不明的地方,还请大神多多指点!