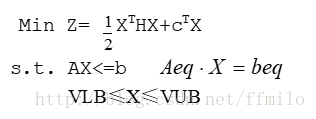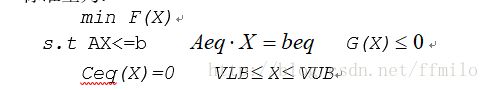matlab优化工具箱笔记(1)
1、线性规划
[x,fval]=linprog(c,A,b,Aeq,Beq,VLB,VUB)
用于解决
min(z)=cX%%求满足条件的X与已定系数c乘积之和的最小值
s.t.
AX<=b %不定约束
AeqX=Beq %定约束
VLB<=X<=VUB %天花板约束
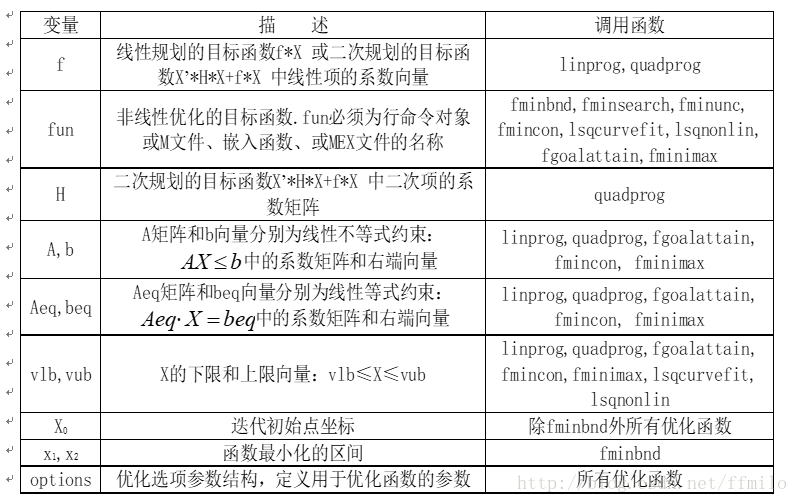
2. matlab优化工具箱求解优化问题的主要函数
3.优化函数的输入变量
4.优化函数的输出变量
5.options的设置
(1)Display (显示水平):
off不显示输出;iter显示每次迭代的信息;final显示最终结果;默认为final;
(2)MaxFunEvals(允许函数评价的最大次数):取值为正整数;
(3)MaxIter(允许进行迭代的最大次数):取值为正整数;
* MaxFunEvals与MaxIter的区别:
(4)FunValCheck:'on' 当目标函数返回值是一个complex、inf、NaN时,显示一个erro;'off'则不显示
(5)TolX;X的退出条件 为一个正的标量。默认为1e-4
MaxFunEvals是目标函数的调用次数,而MaxIter是迭代次数。在一次迭代中,可能需要多次调用目标函数。
options的创建和修改:
options = optimset('param1',value1,'param2',value2,...) %设置所有参数及其值,未设置的为默认值options = optimset %全部设置为默认
options = optimset(optimfun) %设置与最优化函数有关的参数为默认
options = optimset(oldopts,'param1',value1,...) %复制一个已存在的选项,修改特定项
options = optimset(oldopts,newopts) %用另一个新选项合并目前选项
6.一元函数无约束问题求解(fminbnd)%不一定是一次函数
**fminbnd的算法是基于黄金分割法和二次插值法,它要求目标函数必须是连续函数,并可能只给出局部最优解
fimbnd函数:在固定的区间上找到单变量函数的最小值。
(find minimun of single-variable function on fixed interval)
* x1;x2;output(x)都要是标量
常用格式如下:
(1)x= fminbnd (fun,x1,x2)
(2)x= fminbnd (fun,x1,x2 ,options)
(3)[x,fval]= fminbnd(...)
(4)[x,fval,exitflag]= fminbnd(...)
(5)[x,fval,exitflag,output]= fminbnd(...)
例子:
clc;
clear;
%%求解f在x=0~8之间的最小和最大值
%%
%% 第一步:设定函数
f='2*exp(-x).*sin(x)';
f1='-2*exp(-x).*sin(x)';
%% 第二步:优化函数参数设定
options=optimset('Display','iter',...%%显示每次每次迭代的信息
'FunValCheck','on',...%%函数输出值可用性检测
'MaxFunEvals',800,...%%允许函数评价的最多次数
'MaxIter',1000,...%%允许进行迭代的最大次数
'PlotFcns',@optimplotfunccount,...%%图像显示@optimplotx,显示当前x的值;
'TolX',1e-4);%X的终止误差 %%@optimplotfval,显示函数值变化情况
%%@optimplotfunccount,显示函数的计数?
%%计算
[xmin,ymin,exitflag,output]=fminbnd (f, 0,8,options)
%exitflag表示函数退出条件,1-函数找到结果;0-函数最大功能评价次数或者迭代次数达到;-1-算法由外部函数结束
[xmax,ymax]=fminbnd (f1, 0,8,options)
7.多元函数无约束优化问题
多元函数无约束优化问题可以通过两种函数,
1.[x,fval,exitflag,output]=fminunc(fun,x0,options);
2.[x,fval,exitflag,output]=fminsearch(fun,x0,options)
x0可以是标量、向量、矩阵 fun是一个函数句柄
(1)fminsearch 是用单纯形法寻优法
这是一种不会使用数值或者梯度分析的直接的方法。
(2)fminunc:找到非约束多变量函数的最小值。(这里需要补充)
fminunc 为无约束优化提供了大型优化和中型优化算法。由options中参数LargeScale控制:
LargeScale='on',使用大型算法
LargeScale='off',使用中型算法
** fminunc为中型优化算法的搜索方向提供了4中算法,由options中的参数HessUpdate控制
HessUpdate=‘bfgs’(默认值),为拟牛顿的BFGS法
HessUpdate='dfp'为拟牛顿DFP法
HessUpdate=‘steepdesc’最速下降法
**fminunc中为中型优化算法的步长一维搜索提供了两种算法,由options中参数LineSearchType控制,
LineSearchType='quadcubic'混合的二次和三次多项式插值
LineSearchType=‘cubicpoly’三次多项式插值
*使用fminunc和fminsearch都可能会得到局部最优解。
非线性规划の二次规划
标准型为
与线性规划的不同只在于评价函数的不同
用Matlab软件求解,其输入格式如下:
[x,fval,exitflag,output]=quaprog(H,C,A,b,Aeq,Beq,VLB,VUB,X0,options)
一般非线性规划
标准型为:
![]()
用Matlab求解上述问题,基本步骤分为三步:
1、首先建立M文件 fun.m定义目标函数F(X)
function f=fun(x)
f=F(X)
2、若约束条件中由非线性约束:G(X)<=0或Ceq(X)=0,
则建立M文件nonlcon.m定义函数G(X)和Ceq(X)
function [G,Ceq]=nonlcon(X)
G=G(X)
Ceq=Ceq(X)
3、建立主程序,非线性规划求解的函数时fmincon,命令的基本格式如下:
[x,fval,exitflag,output]=fmincon('fun',X0,A,b,Aeq,beq,VLB,VUB,'nonlcon',options)
** fmincon 函数提供了大型优化算法和中型优化算法。 默认时:
若在fun函数中提供了梯度,即GradObj设置为‘on’,并且只有上下界存在或只有等式约束时,
fmincon函数将选择大型算法。如果既有梯度约束又有等式约束的话,那么使用中型算法。
fmincon函数中型算法使用的矢序列二次规划法。即在每一次迭代中求解二次规划子问题,
并用BFGS法更新拉格朗日Hessian矩阵
fmincon函数可能会给出局部最优解,这与初值的选择有关.