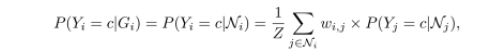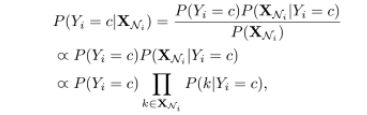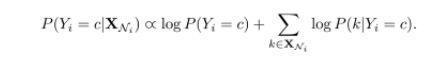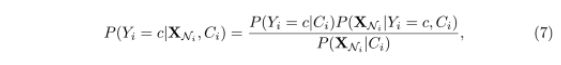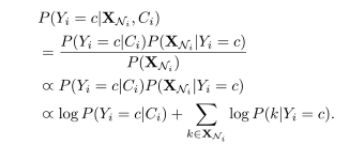重点: 1.基于距离构造带权的query的网络;2. 网络的社区发现,细粒度的。 3. (部分节点有label)根据一阶马尔科夫假设,通过节点本身和相邻节点的信息,构造多项式贝叶斯分类器。对节点进行多标签的分类,从标签的ranking中选择固定个数。粗粒度的。需要预定义好类别,通过一些规则预先标注一些节点。
在搜索中,通过用户的点击,可以收集到很多句子之间的关系,它们彼此连接,形成网络。这个网络中,有些句子也许被标记了类别(分类),大量的节点是未知类别。因此,通过一些其他特征(可能是文本上的),加上网络特征,希望得到更好的分类器。
通常,很多现实中的网络表现出一些有用的现象,如聚类、无标度现象。大部分的网络表现出高度聚类特征或者社群特性。聚类的现象说明可以把网络划分成社区,社区内彼此连接多,社区间彼此连接少。In the dense connected communities , the identifier of neighbors may capture link patterns between nodes. (邻居的标识符可能会补货节点之间的连接模式)。无标度现象,说明了高度节点的存在,而这些节点的分类对于补货local patterns 有帮助。节点标识符作为高密度的特征,提出了基于相邻分类器的识别器,分类器基于一阶马尔科夫假设和社群优先。
首先假设了:一个节点的分类仅仅取决于它的相邻节点及本身。
问题定义:有网络,网络中部分点被标记了,要预估未被标记的节点的label。
L 表示所有节点的label集合。yi 表示节点i的 class lable 取值,yi会被分配到一个类别值,这个值属于L.。Gi表示节点i的信息。P(yi=c|Gi)表示节点i 数据label c的概率。
RN算法中,根据一阶马尔科夫假设, P(yi=c|Gi) = P(yi=c |Ni) 其中, Ni表示节点i 相邻的节点集合。
WvRN算法中,提出了带权重的投票算法。
IDRN 分类器:只考虑节点自己网络内的的节点的识别器,分类器会表现的更好。node identifier ,也就是对于单个的节点进行unique symbols , 提取后被作为特征用于学习和推理。基于一阶马尔科夫假设,简化节点i的信息Gi = G(N) = X(N) = {x | x 属于N} 并{i}。。。
将 i 的信息简化为 一个 特征向量,此向量为以 i 为中心的图 G(N) 的所有点的identifier。 G(N) 是节点i 的一阶区域子图。还考虑了节点本身的identifier。例如,一个节点i ,id 为1。与之相邻的节点为 2,3,5 。那么此节点 的特征向量 X(Ni) = [1,2,3,5]。基于朴素贝叶斯假设(严格的相互独立)
多分类
传统的多分类问题都是转化成one-vs-rest 问题。在训练IDRN分类器时,对于节点i,有多个真实的label值,我们将其转化成一组单label的点。然后,用朴素贝叶斯去训练模型,来预估先验概率 P(yi=c) 和 条件概率P(k | yi=c) 。
以MLE 为目标训练多分类器,多项式朴素贝叶斯的表现常常优于伯努利朴素贝叶斯。
假设我们训练数据中有N个点。Nc 表示 c类别的出现次数,Nkc 表示 feature k 和c 类别的共现次数。算法中,我们首先初始化N,Nc ,Nkc。然后,转换每个节点i(其多标签集合为Ti)到单类别数据。然后利用多项式朴素贝叶斯计算N,Nc ,Nkc。再然后,对每个类别和特征,计算P(Yi=C) 和 P(k|Yi=c)。
多标签预测,目标是为没有标签的数据找到最可能的标签集合。大多数的方法是对label进行ranking而不是精确的分配,这就需要一个阈值。为了避免引入这个阈值,我们给节点分配s个最可能的label,s是设定好的数字。另外,如上式,相乘的形式,一堆概率相乘,数值太小,可能会向下溢出。加上log,变为相加的形式。
先验社区:大家认为社区内的节点,具有相同的一些普通属性,扮演类似的角色。也有人认为相同社区的节点应该具有相似的表达。这些前提假设使我们可以对节点进行更精确的分类,在有有效训练数据的前提下。给定一个网络的社区分布,通过经验计数和加1 平滑方法,就可以预测P(yi=c| Ci) ,Ci 为node i 所属的社区,c 是类别。。
P(XNi | Ci)表示条件概率,而Ci 与XNi 相互独立,因此 P(XNi | Ci) = P(XNi) , P(XNi | Y=c,Ci) = P(XNi | Y=c)。因此
用Louvain 算法从网络中提取社区。