《算法笔记》—— 图 "最短路径" 之 Bellman-Ford 算法

最短路径相关文章：
《算法笔记》—— 图 “最短路径” 之 Floyd-Warshall算法、Diljkstra算法

---

上面链接的文章之中有个算法是 Dilijkstra算法，这个算法解决单源最短路径问题，但是它 不能解决带有负权边（边的权值为负数）的图，原因如下：Dijkstra算法为什么不能用于负权图

此文将介绍 Bellman-Ford算法，它完美了解决负权的这个问题，并且此文将介绍对此算法各种的优化操作，比如：使用队列的方式对此算法进行优化 . . .

---

.

文章目录

• Bellman-Ford 算法解析
• Bellman-Ford 算法优化（1）
• Bellman-Ford 算法优化（2）
• Bellman-Ford 算法优化后的代码
• Bellman-Ford 算法优化 —— 队列优化
• 几种算法的比较

可见，后三个都是基于第一个而来的，说明这个算法是多么的强大 ^ _ ^ . . .

---

.

Bellman-Ford 算法解析

Bellman-Ford 算法核心代码只有4行，可以完美的解决有负权边的图，如下所示：

for(k = 1; k <= n - 1; k++)
    for(i = 1; i <= m; i++)
        if(dis[v[i]] > dis[u[i]] + w[i])
            dis[v[i]] = dis[u[i]] + w[i];

这个算法非常的简单，但我们要清楚其中的意思，比如外循环、内循环、关系比较等 . . .

源码解析：

1. 外循环：n 表示顶点的个数，循环 n - 1次（原因后面会说）
2. 内循环：m 表示边的个数，循环 m次
3. dis数组的作用与 Dijkstra算法中是一样的
4. v u w三个数组表示一个边的信息：起点、终点、权值
5. 后两行的意思：

   if(dis[v[i]] > dis[u[i]] + w[i])
       dis[v[i]] = dis[u[i]] + w[i];

   表示能否通过 u[i] -> v[i]（权值为 w[i]）这条边，使得 1 号顶点到 v[i] 号顶点的距离变短 . . .

上面第五个是基于某一个点来的，如果我们想将每一条边都 “松弛” （上一篇文章有讲）一遍，那么我们只需加一个for即可：

for(i = 1; i <= m; i++)
   if(dis[v[i]] > dis[u[i]] + w[i])
       dis[v[i]] = dis[u[i]] + w[i];

那么我们进行第一轮 “松弛” 会有什么样的效果呢？ 好吧，下面让我们来举个例子来体会一下这个算法的神奇之处 . . .

例如：求出下面图 1 号顶点到其余所有顶点的最短路径。

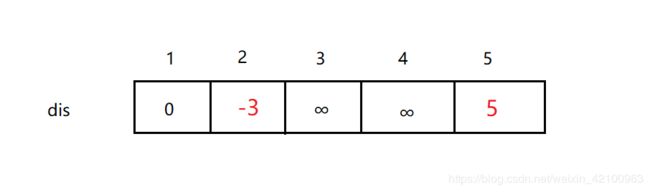
当前的 dis数组中的数据为：

其中 ∞ 表示的是估计值（当前 1 号顶点到该顶点的距离），即数组 dis 中对应的值 . . .

.

现在，我们根据给出的顺序，先来处理第 1 条边 “2 3 2”（2 -> 3，通过这条边进行松弛），即判断 dis[3] > dis[2] + 2 ？ 很显然， 根据上面的 dis数组这个关系式并不能成立 . . .

同理，第 2 条边 “1 2 -3”（1 -> 2），我们发现这条边将松弛成功，所以 dis[2] 从 ∞ 变为 -3，用同样的方法处理剩下的每一条边。如果如下：

我们对每一条边都进行 n - 1 次松弛（n为结点的个数），最后结果为：

说到这里，我们可以会想到两个问题

• 为什么要进行 n - 1次循环呢？
  因为在一个含有 n 个顶点的图中，任意两个顶点之间的最短路径最多包含 n - 1边

• 最短路径中不可能包含回路吗？

  答案是：不可能！！！ 如果最短路径中包含正权回路，那么去掉这个回路，一定可以得到更短的路径。
  如果最短路径中包含负权回路那么肯定没有最短路径，因为每多走一次负权回路就可以得到更短的路径 . . .

Bellman-Ford 算法演示：

#include 
int main()
{
    int dis[10], i, k, n, m;
    int inf = 999999999;
    
    n = m = 5;  // 顶点  边的个数
    
    int u[10] = { 0, 2,1,1,4,3 };  // 起点
    int v[10] = { 0, 3,2,5,5,4 };  // 终点
    int w[10] = { 0, 2,-3,5,2,3 };  // 权值

    for (i = 1; i <= n; i++)	// 初始化为估计值
        dis[i] = inf;
    dis[1] = 0;

    // 对每一条边进行  n - 1 次松弛
    for (k = 1; k <= n - 1; k++) {
        for (i = 1; i <= m; i++) {
    	    if (dis[v[i]] > dis[u[i]] + w[i])
    		dis[v[i]] = dis[u[i]] + w[i];
  	}
    }
    
    for (i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }

    return 0;
}

结果如下：

0 -3 -1 2 4

---

.

Bellman-Ford 算法优化（1）

Bellman-Ford 算法 的作用不仅于此，它还可以检测一个图是否含有负权回路。如果在进行 n - 1 轮松弛之后，仍然存在可以松弛：

if (dis[v[i]] > dis[u[i]] + w[i])
    dis[v[i]] = dis[u[i]] + w[i]; 

那么此图必然存在负权回路的情况，算法优化关键代码如下：

// 算法核心语句
for (k = 1; k <= n - 1; k++) {
   for (i = 1; i <= m; i++) {
       if (dis[v[i]] > dis[u[i]] + w[i])
           dis[v[i]] = dis[u[i]] + w[i];
   }
}
//
// 检测负权回路
int flag = 0;
for(i = 1; i <= m; i++)
   if(dis[v[i]] > dis[u[i]] + w[i]) 
       flag = 1;
if(flag == 1)
   printf("此图是负权回路");

---

.

Bellman-Ford 算法优化（2）

在实际操作中，Bellman-Ford 算法经常会未达到 n - 1轮松弛前就已经计算出所有最短路，之前我们已经说过，n - 1其实是最大值。因此我们需要一个备份数组来判断一下下轮循环 dis中的值是否改变，可以提前跳出循环，提高效率，基本优化如下：

for (k = 1; k <= n - 1; k++) {

    // 保存之前 dis中的值
    for (i = 1; i <= n; i++) bak[i] = dis[i]; 
    
    for (i = 1; i <= m; i++) {
        if (dis[v[i]] > dis[u[i]] + w[i])
            dis[v[i]] = dis[u[i]] + w[i];
    }

    // 开始判断
    int check = 0; 
    for (i = 1; i <= n; i++) {
       if (bak[i] != dis[i]) {
           check = 1;
           break;
       }
    }
    
    if (!check) break;
}

---

.

Bellman-Ford 算法优化后的代码

#include 

int main()
{
    int dis[10], i, k, n, m;
    int inf = 999999999;
    
    n = m = 5;  // 顶点  边的个数
    
    int u[10] = { 0, 2,1,1,4,3 };  // 起点
    int v[10] = { 0, 3,2,5,5,4 };  // 终点
    int w[10] = { 0, 2,-3,5,2,3 };  // 权值
    
    for (i = 1; i <= n; i++)
        dis[i] = inf;
    dis[1] = 0;

    int bak[10];
    for (k = 1; k <= n - 1; k++) {
    
        // 纪录当前  dis的值
        for (i = 1; i <= n; i++) bak[i] = dis[i]; 
    
        // 核心代码
        for (i = 1; i <= m; i++) {
            if (dis[v[i]] > dis[u[i]] + w[i])
                dis[v[i]] = dis[u[i]] + w[i];
        }

        // 没有更新，结点剩余的外循环
        int check = 0; 
        for (i = 1; i <= n; i++) {
            if (bak[i] != dis[i]) {
    	        check = 1;
            	break;
   	    }
        }
        if (!check) break; 
    }

    // 检查是否是负权回路
    int flag = 0;
    for (i = 1; i <= m; i++) {
        if (dis[v[i]] > dis[u[i]] + w[i])
  	{
   	    flag = 1;
   	    break;
  	}
    }
    if (flag) {
        printf("负权回路");
    }
    
    for (i = 1; i <= n; i++) {
       printf("%d ", dis[i]);
    }
    
    return 0;
}

---

.

Bellman-Ford 算法优化 —— 队列优化

我们对每一条边进行 n - 1 次松弛判断，可以其中某一个顶点一直没有变化，这样就提高了算法的复杂度，我们只需要 对最短路径发生变化了的点的相邻执行松弛操作。我们可以用一个队列来维护这些点 . . .

思想如下：

每次选取队首顶点 u，对顶点u 的所有出边进行松弛操作，如果松弛成功，并且没有存在于队列之中，则入队，所有出边结束后，队头出队，进行下一个顶点的判断 . . .

例如下面这个图：

这个图与上面的关系一样，有着起点、终点、权值 . . .

现在我们将顶点 1 放入队列之中，如下所示：

我们发现顶点 1 的出边有顶点2 和 顶点 5，我们对顶点 2 进行松弛操作，比较 dis[2] 和 dis[1] + (1 -> 2）的大小，容易知道松弛成功。同理，顶点 5 也松弛成功。因此， 队头为 顶点1 的所有操作已经完成， dis 数组 和 que 队列的数据如下所示：

队头出队，然后重复上面的操作，直至队列中无数据，最终数组 dis 和 队列 que 状态如下：

.

代码实现队列优化算法，用邻接表来存储这个图，操作如下：

#include 

int main()
{
    int n, m, i, j, k;
    int u[8], v[8], w[8];	// 起点、终点、权值
    
    int first[6] = { 0 }, next[8] = { 0 };      // 用于构建邻接表
    int dis[6] = { 0 }, book[6] = { 0 };  // 存储路径 与 标记
    int que[101] = { 0 }, head = 1, tail = 1; // 队列完成此例
    
    int inf = 999999999;      // inf 表示无穷大

    scanf("%d%d", &n, &m);      // 顶点与边的数量
    for (i = 1; i <= n; i++) {	// 初始点的估计值
        dis[i] = inf;
    }
    dis[1] = 0;         // 一号顶点就位
    
    for (i = 1; i <= n; i++) {
        first[i] = -1;       // 表示所有的顶点当前没有边
    }

    for (i = 1; i <= m; i++) {
        scanf("%d%d%d", &u[i], &v[i], &w[i]);
	
	// 形成邻接表的关键
	// first[u[i]] 保存顶点 u[i] 的第一条边的编号
	// next[i] 存储 "编号为 i 的边" 的 "下一条边" 的编号
  	next[i] = first[u[i]];
  	first[u[i]] = i;
    }

    que[tail++] = 1;
    book[1] = 1;         // 1号顶点标记

    while (head < tail) {
    
        k = first[que[head]];      // 当前需要处理的队首顶点
        while (k != -1) {
            if (dis[v[k]] > dis[u[k]] + w[k]) {  // 判断是否可以松弛
    	        dis[v[k]] = dis[u[k]] + w[k];  // 更新路径 
    	        if (book[v[k]] == 0)    // 判断是否已经存在于队列之中
    	        {
     	            que[tail++] = v[k];    // 当前点入队
       	            book[v[k]] = 1;     // 标记当前点
    	        }
            }
            k = next[k];
        }
        book[que[head]] = 0;      // 可能会有重复的顶点入队
        head++;          // 出队
    }

    for (i = 1; i <= n; i++){
        printf("%d ", dis[i]);
    }   

    return 0;
}

---

.

几种算法的比较

---

文章可能写的比较粗略，比较模糊的可以私聊我 ^ _ ^

作者：浪子花梦