常用排序算法汇总(一)
前言:
在阅读了《算法第四版》排序部分后,由于很久没有看导致啥都忘记了,故在此对其中的算法原理以及Java实现整理一下,方便以后自己复习。
在此顺便推荐一个排序算法可视化网站,搞不明白原理可全靠他了,调下倍速,慢慢体会其中的奥秘!网址如下:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
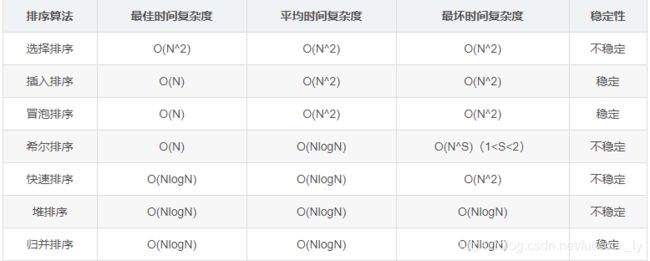
以下是常见排序算法的时间复杂度以及稳定性:
选择排序
对于选择排序,用比较官方的定义,是通过n-i次关键字间的比较,从n-i+1个记录里选出关键字最小的记录,并和第i(1<=i<=n)个记录进行交换。
笼统一点呢,就是首先找到数组中最小的那个元素,其次,将他和数组的第一个元素交换位置(如果第一个是最小元素就跟自己交换)。再次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此反复,直到将整个数组排序。
分析时间复杂度,无论最好最差的情况,其比较次数都一样多为n(n-1)/2,而对于交换次数来说,最好的情况是0次,最差是n-1次。
基于最终的排序时间是比较与交换的次数总和,因此,总的时间复杂度依然为O(n^2)
public class Selection {
public static void sort(Comparable[] a){
int N=a.length;
for(int i=0;i<N;i++){
int min=i;
for(int j=i+1;j<N;j++)
if(less(a[j],a[min])) min=j;
exch(a,i,min);
}
}
//用于判断两个元素的大小
//less()方法,前者大于等于后者时返回0,前者小于后者时返回1;
//compareTo()方法,v>w时返回1,相等时返回0,v
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
//用于交换两个元素
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
//打印每一个元素
private static void show(Comparable[] a){
for(int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
System.out.println();
}
//判断数组是否排序完成
public static boolean isSorted(Comparable[] a){
for(int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;//前者大于后者时,返回false
return true;//排序正确时返回true
}
public static void main(String[] args) {
String[] a={"bed","bug","yes","zoo","panda","all","yet","shit"};
sort(a);
assert isSorted(a);
show(a);
}
}
插入排序
插入排序就像人们整理桥牌的方法,一张一张地来,将每一张牌插入到其他已经有序的牌中的适当位置。为了给要插入的元素腾出空间,我们需要将其余所有元素在插入之前都向右移动一位,这种算法叫做插入排序。
代码由两个简单的嵌套循环组成,注意以i所在的进行分割,i指针所在位置就是即将插入的数据,左边即为有序数组,右边为无序数组,内层循环将a[i]与上一元素进行比较,如果比上一元素小即交换位置,直至上一元素比当前元素小为止。如此循环,当i指针移动到数组的最后一个元素时,则结束排序。注意:i的取值应该从1开始。
插入的交换次数和比较次数和待排序数组中“倒置”的数量紧密相关,所谓倒置,指的是数组中的两个顺序颠倒的元素,比如待排序数组中15在9的前面,说明他们需要交换位置才能达到排序的目的(假设从小到大排序),那么15-9就算是一对倒置的元素。插入排序的交换次数和倒置的数量相同,需要的比较次数大于等于倒置的数量,小于等于倒置的数量 加上数组的大小再减1.
总的来说,插入排序的时间复杂度还是O(n^2)
public class Insertion {
//将未排序数据插入已排好序列中的合适位置
//每次加入一个数据,移动到合适位置
public static void sort(Comparable[] a){
int N=a.length;
for(int i=1;i<N;i++){
for(int j=i;j>0&&less(a[j],a[j-1]);j--)
exch(a,j,j-1);
}
}
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
//compareTo()方法,v>w时返回1,相等时返回0,v
//less()方法,前者大于等于后者时返回0,前者小于后者时返回1;
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a){
for(int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
System.out.println();
}
public static boolean isSorted(Comparable[] a){
for(int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;//前者大于后者时,返回false
return true;//排序正确时返回true
}
public static void main(String[] args) {
String[] a={"bed","bug","yes","zoo","panda","all","yet","shit"};
sort(a);
assert isSorted(a);
show(a);
}
}
希尔排序
希尔排序是一种基于插入排序的快速的排序方法,其思想是使数组中任意间隔为h的元素都是有序的,这样的数组被称为h有序数组。换句话说,一个h有序数组就是h个互相独立的有序数组编制在一起组成的一个数组。
实现希尔排序的一种方法是对于每个h,用插入排序将h个子数组独立地排序。但因为子数组是相互独立的,一种更简单的方法是在h-子数组中将每个元素交换到比它大的元素之前去(将比他大的元素向右移动一格),只需要在插入排序的代码中将移动元素的距离由1改为h即可。
public class Shell {
public static void sort(Comparable[] a){
int N=a.length;
int h=1;
while(h<N/3) h=3*h+1;//1,4,13,40,121,364,1093....
while(h>=1){
for(int i=h;i<N;i++) {
for (int j = i; j >= h && less(a[j], a[j - h]); j -= h)
exch(a, j, j - h);
}
h=h/3;
}
}
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
//compareTo()方法,v>w时返回1,相等时返回0,v
//less()方法,前者大于等于后者时返回0,前者小于后者时返回1;
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a){
for(int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
System.out.println();
}
public static boolean isSorted(Comparable[] a){
for(int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;//前者大于后者时,返回false
return true;//排序正确时返回true
}
public static void main(String[] args) {
String[] a={"bed","bug","yes","zoo","panda","all","yet","shit"};
sort(a);
assert isSorted(a);
show(a);
}
}
归并排序
归并排序是一类总称,其思想是将一个数组排序,可以先递归地将它分成两半分别排序,然后将结果归并起来。归并排序最大的优势是它能够保证将任意长度为N的数组排序所需时间和NlogN成正比;它的主要缺点则是它所需的额外空间和N成正比(需要一个辅助数组)。
代码中的Merge方法,就是合并两个有序数组的过程。而sort方法,则是将每一个数组都进行分割排序,当数组的元素数量小于4个时,则使用插入排序来提高效率。
public class MergeSort {
private static Comparable[] aux;
public static void sort(Comparable[] a){
aux=new Comparable[a.length];
sort(a,0,a.length-1);
}
public static void sort(Comparable[] a,int lo,int hi){
//将数组a[lo,hi]排序
if(hi<=lo) return;
if(hi-lo<=4) Insertion.sort(a);//当数组中元素过少时,使用插入排序以节省空间
int mid=lo+(hi-lo)/2;
sort(a,0,mid);
sort(a,mid+1,hi);
if(less(a[mid],a[mid+1])) return;//如果第一个有序子数组的最后一位小于第二个的第一位,跳过归并操作。
merge(a,lo,hi,mid);
}
public static void merge(Comparable[] a,int lo,int hi,int mid) {
//将a[lo,mid]和a[mid+1,hi]进行归并
int i = lo, j = mid + 1;
//将数组a的数组都复制到数组aux里
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
for (int p = lo; p <= hi; p++) {
if (i > mid) a[p] = aux[j++];
else if (j > hi) a[p] = aux[i++];
else if (less(aux[i], aux[j])) a[p] = aux[i++];
else a[p] = aux[j++];
}
}
//最后一个改进在于节省元素拷贝到辅助数组的时间,每一次递归时转换一下原数组和辅助数组的位置
// public static void sort(Comparable[] a,Comparable[] aux,int lo,int hi){
// //将数组a[lo,hi]排序
// if(hi<=lo) return;
// int mid=lo+(hi-lo)/2;
// sort(aux,a,lo,mid);
// sort(aux,a,mid+1,hi);
// merge(a,aux,lo,hi,mid);
//
// }
// public static void merge(Comparable[] aux,int lo,int hi,int mid){
// //将a[lo,mid]和a[mid+1,hi]进行归并
// int i=lo,j=mid+1;
// //将数组a的数组都复制到数组aux里
// for(int k=lo;k<=hi;k++){
// aux[k]=a[k];
// }
// for(int p=lo;p<=hi;p++) {
// if (i > mid) aux[p] = a[j++];
// else if (j > hi) aux[p] = a[i++];
// else if (less(aux[i], aux[j])) aux[p]=a[i++];
// else aux[p]=a[j++];
// }
// }
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
//compareTo()方法,v>w时返回1,相等时返回0,v
//less()方法,前者大于等于后者时返回0,前者小于后者时返回1;
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a){
for(int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
System.out.println();
}
public static boolean isSorted(Comparable[] a){
for(int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;//前者大于后者时,返回false
return true;//排序正确时返回true
}
public static void main(String[] args) {
String[] a={"bed","bug","yes","zoo","panda","all","yet","shit"};
sort(a);
if(!isSorted(a)) System.out.println("haimei");
show(a);
}
}
快速排序
快速排序可能是应用最广泛的排序算法了,它实现简单,适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。快速排序的最大优点是它是原地排序(只需要一个很小的辅助栈),且将长度为N的数组排序所需的时间和NlgN成正比。
对于快速排序,还是比较不好理解的,上个写的不错的文章嘻嘻,动图和漫画详解快速排序。
快速排序首先要选择一个基准数,可以是第一位,然后数组左右边两个“哨兵”同时向中间移动,并把小于基准数的元素和大于基准数的元素做交换,当左右哨兵相遇时,将基准数与其交换。这样,以基准数为标志,在基准数左边的,都是比他小的元素,在基准数右边的,都是比他大的元素。然后再递归对这两个子数组进行处理,直至完全有序。
import edu.princeton.cs.algs4.StdRandom;
/**
* @Author:LinYuan
* @Description:
* @Date: Create in 11:26 2019/7/31
* @Modified By:
*/
public class QuickSort {
public static void sort(Comparable[] a){
StdRandom.shuffle(a);
sort(a,0,a.length-1);
}
private static void sort(Comparable[] a,int lo,int hi){
if(hi<=lo) return;
int t=partition(a,lo,hi);
sort(a,lo,t-1);
sort(a,t+1,hi);
}
private static int partition(Comparable[] a,int lo,int hi){
int k=lo,i=lo,j=hi+1;
while(true){
while(less(a[++i],a[k])) if(i==hi) break;
while(less(a[k],a[--j])) if(j==lo) break;
if(i>=j) break;
exch(a,i,j);
}
exch(a,lo,j);
return j;
}
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
//compareTo()方法,v>w时返回1,相等时返回0,v
//less()方法,前者大于等于后者时返回0,前者小于后者时返回1;
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a){
for(int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
System.out.println();
}
public static boolean isSorted(Comparable[] a){
for(int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;//前者大于后者时,返回false
return true;//排序正确时返回true
}
public static void main(String[] args) {
String[] a={"bed","bug","yes","zoo","panda","all","yet","shit"};
sort(a);
assert isSorted(a);
show(a);
}
}