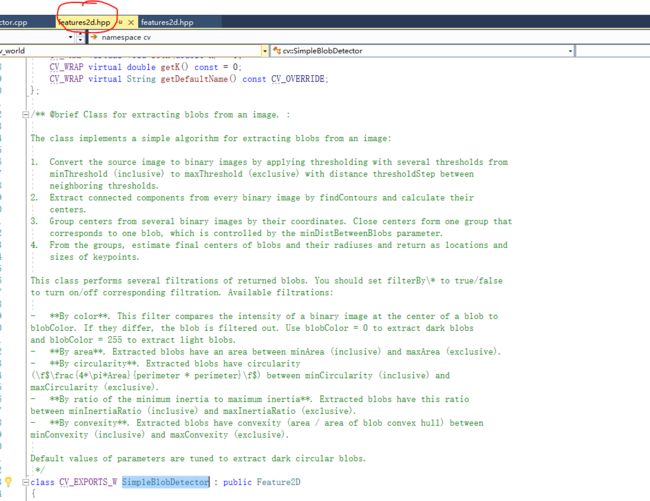
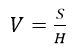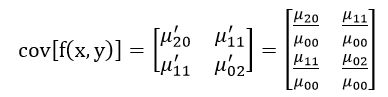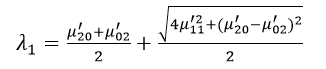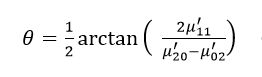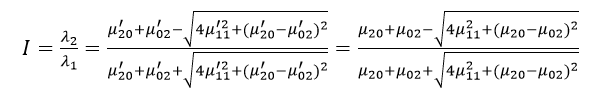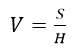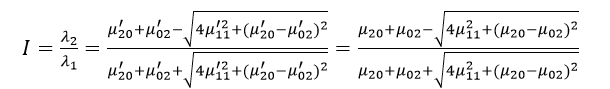一、blob基础
所谓Blob就是图像中一组具有某些共同属性（例如，灰度值）的连接像素。在上图中，深色连接区域是斑点，斑点检测的目的是识别并标记这些区域。OpenCV提供了一种方便的方法来检测斑点并根据不同的特征对其进行过滤。在OpenCV 3中，使用SimpleBlobDetector :: create方法创建智能指针调用该算法。
Python
Python
# Setup SimpleBlobDetector parameters.
params
=
cv2.SimpleBlobDetector_Params()
# Change thresholds
params.minThreshold
=
10
;
params.maxThreshold
=
200
;
# Filter by Area.
params.filterByArea
=
True
params.minArea
=
1500
# Filter by Circularity
params.filterByCircularity
=
True
params.minCircularity
=
0
.
1
# Filter by Convexity
params.filterByConvexity
=
True
params.minConvexity
=
0
.
87
# Filter by Inertia
params.filterByInertia
=
True
params.minInertiaRatio
=
0
.
01
# Create a detector with the parameters
ver
=
(cv2.
__version__
).split(
'.'
)
if
int
(ver[
0
])
<
3
:
detector
=
cv2.SimpleBlobDetector(params)
else
:
detector
=
cv2.SimpleBlobDetector_create(params)
C++
// Setup SimpleBlobDetector parameters.
SimpleBlobDetector
:
:Params params;
// Change thresholds
params.minThreshold
=
10;
params.maxThreshold
=
200;
// Filter by Area.
params.filterByArea
=
true;
params.minArea
=
1500;
// Filter by Circularity
params.filterByCircularity
=
true;
params.minCircularity
=
0.
1;
// Filter by Convexity
params.filterByConvexity
=
true;
params.minConvexity
=
0.
87;
// Filter by Inertia
params.filterByInertia
=
true;
params.minInertiaRatio
=
0.
01;
#
if CV_MAJOR_VERSION
<
3
// If you are using OpenCV 2
// Set up detector with params
SimpleBlobDetector detector(params);
// You can use the detector this way
// detector.detect( im, keypoints);
#
else
// Set up detector with params
Ptr
<SimpleBlobDetector
> detector
= SimpleBlobDetector
:
:create(params);
// SimpleBlobDetector::create creates a smart pointer.
// So you need to use arrow ( ->) instead of dot ( . )
// detector->detect( im, keypoints);
#
endif
二、blob参数设置
在OpenCV中实现的叫做SimpleBlobDetector，它基于以下描述的相当简单的算法，并且进一步由参数控制，具有以下步骤。
SimpleBlobDetector
:
:Params
:
:Params()
{
thresholdStep
=
10;
//二值化的阈值步长，即公式1的t
minThreshold
=
50;
//二值化的起始阈值，即公式1的T1
maxThreshold
=
220;
//二值化的终止阈值，即公式1的T2
//重复的最小次数，只有属于灰度图像斑点的那些二值图像斑点数量大于该值时，该灰度图像斑点才被认为是特征点
minRepeatability
=
2;
//最小的斑点距离，不同二值图像的斑点间距离小于该值时，被认为是同一个位置的斑点，否则是不同位置上的斑点
minDistBetweenBlobs
=
10;
filterByColor
=
true;
//斑点颜色的限制变量
blobColor
=
0;
//表示只提取黑色斑点；如果该变量为255，表示只提取白色斑点
filterByArea
=
true;
//斑点面积的限制变量
minArea
=
25;
//斑点的最小面积
maxArea
=
5000;
//斑点的最大面积
filterByCircularity
=
false;
//斑点圆度的限制变量，默认是不限制
minCircularity
=
0.
8f;
//斑点的最小圆度
//斑点的最大圆度，所能表示的float类型的最大值
maxCircularity
= std
:
:numeric_limits
<
float
>
:
:max();
filterByInertia
=
true;
//斑点惯性率的限制变量
minInertiaRatio
=
0.
1f;
//斑点的最小惯性率
maxInertiaRatio
= std
:
:numeric_limits
<
float
>
:
:max();
//斑点的最大惯性率
filterByConvexity
=
true;
//斑点凸度的限制变量
minConvexity
=
0.
95f;
//斑点的最小凸度
maxConvexity
= std
:
:numeric_limits
<
float
>
:
:max();
//斑点的最大凸度
}
SimpleBlobDetector
:
:Params
:
:Params()
{
thresholdStep = 10; //二值化的阈值步长，即公式1的t
minThreshold = 50; //二值化的起始阈值，即公式1的T1
maxThreshold = 220; //二值化的终止阈值，即公式1的T2
//重复的最小次数，只有属于灰度图像斑点的那些二值图像斑点数量大于该值时，该灰度图像斑点才被认为是特征点
minRepeatability = 2;
//最小的斑点距离，不同二值图像的斑点间距离小于该值时，被认为是同一个位置的斑点，否则是不同位置上的斑点
minDistBetweenBlobs = 10;
filterByColor = true; //斑点颜色的限制变量
blobColor = 0; //表示只提取黑色斑点；如果该变量为255，表示只提取白色斑点
filterByArea = true; //斑点面积的限制变量
minArea = 25; //斑点的最小面积
maxArea = 5000; //斑点的最大面积
filterByCircularity = false; //斑点圆度的限制变量，默认是不限制
minCircularity = 0. 8f; //斑点的最小圆度
//斑点的最大圆度，所能表示的float类型的最大值
maxCircularity = std : :numeric_limits < float > : :max();
filterByInertia = true; //斑点惯性率的限制变量
minInertiaRatio = 0. 1f; //斑点的最小惯性率
maxInertiaRatio = std : :numeric_limits < float > : :max(); //斑点的最大惯性率
filterByConvexity = true; //斑点凸度的限制变量
minConvexity = 0. 95f; //斑点的最小凸度
maxConvexity = std : :numeric_limits < float > : :max(); //斑点的最大凸度
}
{
thresholdStep = 10; //二值化的阈值步长，即公式1的t
minThreshold = 50; //二值化的起始阈值，即公式1的T1
maxThreshold = 220; //二值化的终止阈值，即公式1的T2
//重复的最小次数，只有属于灰度图像斑点的那些二值图像斑点数量大于该值时，该灰度图像斑点才被认为是特征点
minRepeatability = 2;
//最小的斑点距离，不同二值图像的斑点间距离小于该值时，被认为是同一个位置的斑点，否则是不同位置上的斑点
minDistBetweenBlobs = 10;
filterByColor = true; //斑点颜色的限制变量
blobColor = 0; //表示只提取黑色斑点；如果该变量为255，表示只提取白色斑点
filterByArea = true; //斑点面积的限制变量
minArea = 25; //斑点的最小面积
maxArea = 5000; //斑点的最大面积
filterByCircularity = false; //斑点圆度的限制变量，默认是不限制
minCircularity = 0. 8f; //斑点的最小圆度
//斑点的最大圆度，所能表示的float类型的最大值
maxCircularity = std : :numeric_limits < float > : :max();
filterByInertia = true; //斑点惯性率的限制变量
minInertiaRatio = 0. 1f; //斑点的最小惯性率
maxInertiaRatio = std : :numeric_limits < float > : :max(); //斑点的最大惯性率
filterByConvexity = true; //斑点凸度的限制变量
minConvexity = 0. 95f; //斑点的最小凸度
maxConvexity = std : :numeric_limits < float > : :max(); //斑点的最大凸度
}
- 阈值：通过使用以minThreshold开始的阈值对源图像进行阈值处理，将源图像转换为多个二进制图像。这些阈值以thresholdStep递增，直到maxThreshold。因此，第一个阈值为minThreshold，第二个阈值为minThreshold + thresholdStep，第三个阈值为minThreshold + 2 x thresholdStep，依此类推；
- 分组：在每个二进制图像中，连接的白色像素被分组在一起。我们称这些二进制blob；
- 合并：计算二进制图像中二进制斑点的中心，并合并比minDistBetweenBlob更近的斑点；
- 中心和半径计算：计算并返回新合并的Blob的中心和半径。
并且可以进一步设置SimpleBlobDetector的参数来过滤所需的Blob类型。
- 按颜色：首先需要设置filterByColor =True。设置blobColor = 0可选择较暗的blob，blobColor = 255可以选择较浅的blob。
- 按大小：可以通过设置参数filterByArea = 1以及minArea和maxArea的适当值来基于大小过滤blob。例如。设置minArea = 100将滤除所有少于100个像素的斑点。
- 按圆度：这只是测量斑点距圆的距离。例如。正六边形的圆度比正方形高。要按圆度过滤，请设置filterByCircularity =1。然后为minCircularity和maxCircularity设置适当的值。圆度定义为（
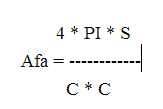）。圆的为圆度为1，正方形的圆度为PI/4，依此类推。
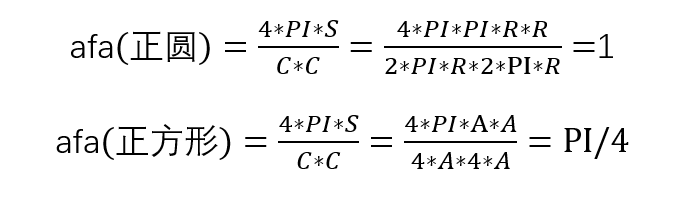
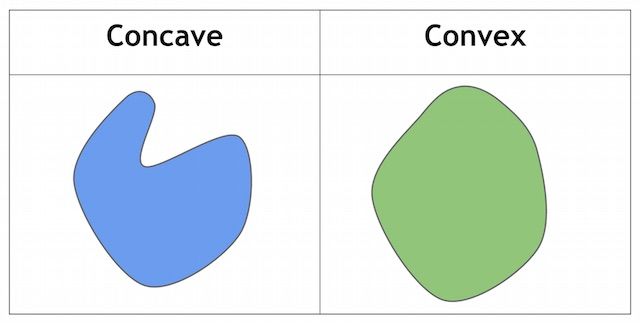
- 按凸性：凸度定义为（斑点的面积/凸包的面积）。现在，形状的“凸包”是最紧密的凸形，它完全包围了该形状，用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。直观感受上，凸性越高则里面“奇怪的部分”越少。要按凸度过滤，需设置filterByConvexity = true，minConvexity、maxConvexity应该属于[0,1]，而且maxConvexity> minConvexity。
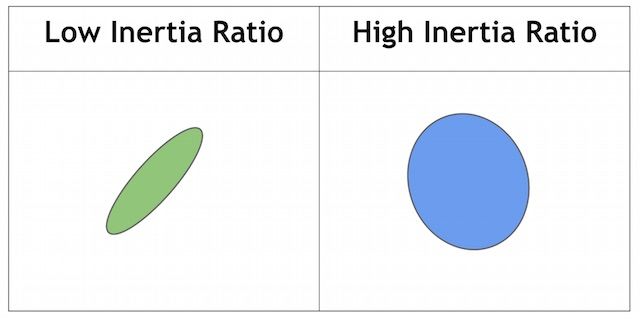
- 按惯性比：这个词汇比较抽象。我们需要知道Ratio可以衡量形状的伸长程度。简单来说。对于圆，此值是1，对于椭圆，它在0到1之间，对于直线，它是0。按惯性比过滤，设置filterByInertia = true，并设置minInertiaRatio、maxInertiaRatio同样属于[0,1]并且maxConvexity> minConvexity。
按凸性（左低右高）
按惯性比（左低右高）
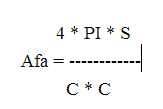）。圆的为圆度为1，正方形的圆度为PI/4，依此类推。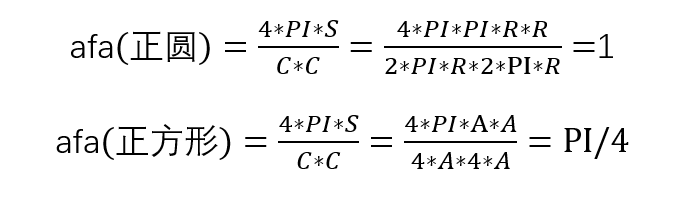| 按凸性（左低右高） | 按惯性比（左低右高） |
| |
|
三、OpenCV的blob代码解析
在它的函数定义部分(feature2d.hpp),详细地说明了该部分代码的使用方法。
实现部分代码，来源于
单文件构成，结构比较简单，主要函数集中于detect和
findBlobs
，其他的皆为配合函数。
主要的一个数据结构，
包含了中心的位置、半径和确定性。
struct CV_EXPORTS Center
{
Point2d location;
double radius;
double confidence;
};
2.1 findblob函数实现
findblob的主要过程是寻找到当前图片的轮廓，而后根据参数中的相关定义进行筛选。其中值得注意的地方。
std::vector < std::vector<Point> > contours;
findContours(binaryImage, contours, RETR_LIST, CHAIN_APPROX_NONE);
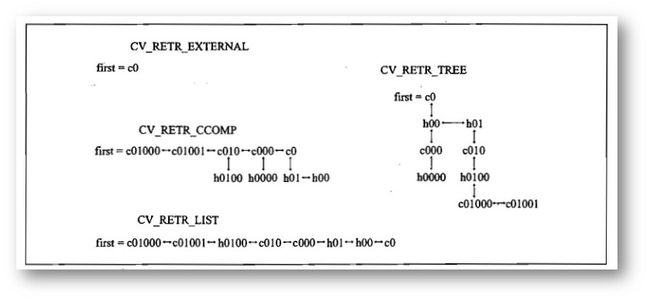
2.1.1在findContours的过程中，使用的是
RETR_LIST 和
CHAIN_APPROX_NONE
，我们来看下图
RETR_LIST
的方法是将所有的轮廓全部以链表的形式串联起来（反过来说，将丢失轮廓间的树状结构）。
2.1.2注意
轮廓遍历的大循环。进入循环后将根据参数中的每一个单项进行逐条筛选。
for (size_t contourIdx = 0; contourIdx < contours.size(); contourIdx++)
{……
2.1.3
“面积”筛选
通过
获得moms.m00
来获得面积。
Moments moms
= moments(contours[contourIdx]);
if (params.filterByArea)
{
double area
= moms.m00;
if (area
< params.minArea
|| area
>
= params.maxArea)
continue;
}
这个地方调用了moments()，该函数用于计算中心矩。
设f(x,y)是一幅数字图像，
，我们把像素的坐标看成是一个二维随机变量(X, Y)，那么一副灰度图可以用二维灰度图密度函数来表示，因此可以用矩来描述灰度图像的特征。
对于二值图像的来说，零阶矩M00等于它的面积，同时一阶矩计算质心/重心。OpenCV中是这样实现
Moments moments(InputArray array,
bool binaryImage
=
false )
class Moments
{
public
:
Moments();
Moments(
double m00,
double m10,
double m01,
double m20,
double m11,
double m02,
double m30,
double m21,
double m12,
double m03 );
Moments(
const CvMoments
& moments );
operator CvMoments()
const;
}
参数说明
- 输入参数：array是一幅单通道，8-bits的图像，或一个二维浮点数组(Point of Point2f)。binaryImage用来指示输出图像是否为一幅二值图像，如果是二值图像，则图像中所有非0像素看作为1进行计算。
- 输出参数：moments是一个类：
2.1.3
“圆度”筛选时通过来计算圆度公式，此外自带函数
arcLength
获得轮廓的周长。
double perimeter
= arcLength(contours[contourIdx],
true);
double ratio
=
4
* CV_PI
* area
/ (perimeter
* perimeter);
2.1.3“颜色”筛选，只判断“圆心”的颜色。
if (params.filterByColor)
{
if (binaryImage.at
<uchar
> (cvRound(center.location.y), cvRound(center.location.x))
!= params.blobColor)
continue;
}
这个使用方法值得商榷，在实际使用过程中不采纳。
2.1.4
"凸性"筛选，
凸图像在0-1之间取值。
if (params.filterByConvexity)
{
std
:
:vector
< Point
> hull;
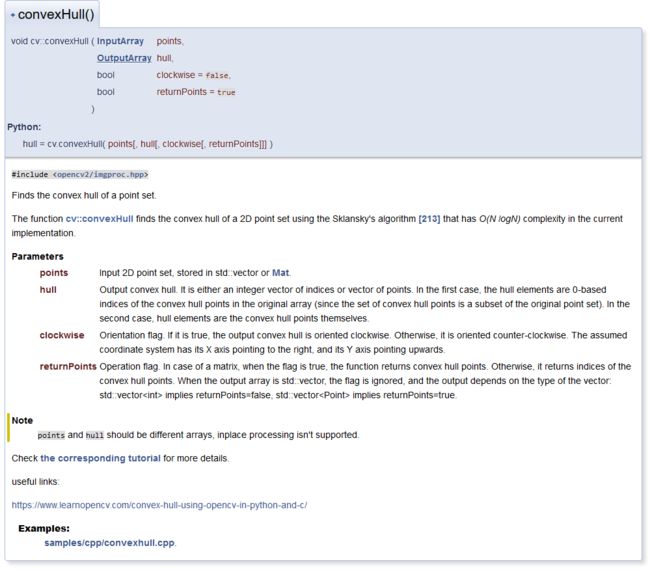
convexHull(contours[contourIdx], hull);
double area
= contourArea(contours[contourIdx]);
double hullArea
= contourArea(hull);
if (fabs(hullArea)
< DBL_EPSILON)
continue;
double ratio
= area
/ hullArea;
if (ratio
< params.minConvexity
|| ratio
>
= params.maxConvexity)
continue;
}
……
我们可以用凸度来表示斑点凹凸的程度，凸度V的定义为：
。其中，使用到了内部函数convexHull
 |
 |
2.1.5“惯性比”筛选，简单的来说，就是轮廓“扁”的程度。对于圆，此值是1，对于椭圆，它在0到1之间，对于直线，它是0。基本上就是取值在0-1之间，越扁越小。
if (params.filterByInertia)
{
double denominator
= std
:
:sqrt(std
:
:pow(
2
* moms.mu11,
2)
+ std
:
:pow(moms.mu20
- moms.mu02,
2));
const
double eps
=
1e
-
2;
double ratio;
if (denominator
> eps)
{
double cosmin
= (moms.mu20
- moms.mu02)
/ denominator;
double sinmin
=
2
* moms.mu11
/ denominator;
double cosmax
=
-cosmin;
double sinmax
=
-sinmin;
double imin
=
0.
5
* (moms.mu20
+ moms.mu02)
-
0.
5
* (moms.mu20
- moms.mu02)
* cosmin
- moms.mu11
* sinmin;
double imax
=
0.
5
* (moms.mu20
+ moms.mu02)
-
0.
5
* (moms.mu20
- moms.mu02)
* cosmax
- moms.mu11
* sinmax;
ratio
= imin
/ imax;
}
else
{
ratio
=
1;
}
if (ratio
< params.minInertiaRatio
|| ratio
>
= params.maxInertiaRatio)
continue;
center.confidence
= ratio
* ratio;
}
……
二阶中心矩称为惯性矩。如果仅考虑二阶中心矩的话，则图像完全等同于一个具有确定的大小、方向和离心率，以图像质心为中心且具有恒定辐射度的椭圆。图像的协方差矩阵为：
该矩阵的两个特征值λ1和λ2对应于图像强度（即椭圆）的主轴和次轴：
而图像的方向角度θ为：
图像的惯性率I为：
这个函数定义和代码略有不同，没有进一步研究。
2.1.6特别注意“半径”的计算方法
//compute blob radius
{
std
:
:vector
<
double
> dists;
for (size_t pointIdx
=
0; pointIdx
< contours[contourIdx].size(); pointIdx
++)
{
Point2d pt
= contours[contourIdx][pointIdx];
dists.push_back(norm(center.location
- pt));
}
std
:
:sort(dists.begin(), dists.end());
center.radius
= (dists[(dists.size()
-
1)
/
2]
+ dists[dists.size()
/
2])
/
2.;
}
采用的是排序取中间值的方法，值得借鉴。
2.2 detect函数实现
2.2.1
对于图像通道的判断，值得借鉴。
Mat grayscaleImage;
if (image.channels()
==
3
|| image.channels()
==
4)
cvtColor(image, grayscaleImage, COLOR_BGR2GRAY);
else
grayscaleImage
= image.getMat();
if (grayscaleImage.type()
!= CV_8UC1) {
CV_Error(Error
:
:StsUnsupportedFormat,
"Blob detector only supports 8-bit images!");
}
2.2.2最外层的循环采用的是遍历阈值的方法，该方法非常值得借鉴。
for (
double thresh
= params.minThreshold; thresh
< params.maxThreshold; thresh
+= params.thresholdStep)
{
Mat binarizedImage;
threshold(grayscaleImage, binarizedImage, thresh,
255, THRESH_BINARY);……
2.2.3
通过距离判断新找到的圆是否为新圆，这段绝对是值得复用的。
for (
double thresh
= params.minThreshold; thresh
< params.maxThreshold; thresh
+= params.thresholdStep)
{
Mat binarizedImage;
threshold(grayscaleImage, binarizedImage, thresh,
255, THRESH_BINARY);
std
:
:vector
< Center
> curCenters;
findBlobs(grayscaleImage, binarizedImage, curCenters);
std
:
:vector
< std
:
:vector
<Center
>
> newCenters;
for (size_t i
=
0; i
< curCenters.size(); i
++)
{
bool isNew
=
true;
for (size_t j
=
0; j
< centers.size(); j
++)
{
double dist
= norm(centers[j][ centers[j].size()
/
2 ].location
- curCenters[i].location);
isNew
= dist
>
= params.minDistBetweenBlobs
&& dist
>
= centers[j][ centers[j].size()
/
2 ].radius
&& dist
>
= curCenters[i].radius;
if (
!isNew)
{
centers[j].push_back(curCenters[i]);
size_t k
= centers[j].size()
-
1;
while( k
>
0
&& curCenters[i].radius
< centers[j][k
-
1].radius )
{
centers[j][k]
= centers[j][k
-
1];
k
--;
}
centers[j][k]
= curCenters[i];
break;
}
}
if (isNew)
newCenters.push_back(std
:
:vector
<Center
> (
1, curCenters[i]));
}
std
:
:copy(newCenters.begin(), newCenters.end(), std
:
:back_inserter(centers));
}
三、一些联想
1、面积筛选这块，那个面积函数是什么意思？
面积函数是专门有实现的。
double cv::contourArea( InputArray _contour, bool oriented )
{
CV_INSTRUMENT_REGION();
Mat contour = _contour.getMat();
int npoints = contour.checkVector(2);
int depth = contour.depth();
CV_Assert(npoints >= 0 && (depth == CV_32F || depth == CV_32S));
if( npoints == 0 )
return 0.;
double a00 = 0;
bool is_float = depth == CV_32F;
const Point* ptsi = contour.ptr<Point>();
const Point2f* ptsf = contour.ptr<Point2f>();
Point2f prev = is_float ? ptsf[npoints-1] : Point2f((float)ptsi[npoints-1].x, (float)ptsi[npoints-1].y);
for( int i = 0; i < npoints; i++ )
{
Point2f p = is_float ? ptsf[i] : Point2f((float)ptsi[i].x, (float)ptsi[i].y);
a00 += (double)prev.x * p.y - (double)prev.y * p.x;
prev = p;
}
a00 *= 0.5;
if( !oriented )
a00 = fabs(a00);
return a00;
}
但是据说，
double
area
=
moms
.
m00
;
也行，这个是为什么？
进入看看，并且删除多余的东西：
cv::Moments cv::moments( InputArray _src, bool binary )
{
CV_INSTRUMENT_REGION();
const int TILE_SIZE = 32;
MomentsInTileFunc func = 0;
uchar nzbuf[TILE_SIZE*TILE_SIZE];
Moments m;
int type = _src.type(), depth = CV_MAT_DEPTH(type), cn = CV_MAT_CN(type);
Size size = _src.size();
if( size.width <= 0 || size.height <= 0 )
return m;
#ifdef HAVE_OPENCL
CV_OCL_RUN_(type == CV_8UC1 && _src.isUMat(), ocl_moments(_src, m, binary), m);
#endif
Mat mat = _src.getMat();
if( mat.checkVector(2) >= 0 && (depth == CV_32F || depth == CV_32S))
return contourMoments(mat);
if( cn > 1 )
CV_Error( CV_StsBadArg, "Invalid image type (must be single-channel)" );
CV_IPP_RUN(!binary, ipp_moments(mat, m), m);
if( binary || depth == CV_8U )
func = momentsInTile<uchar, int, int>;
else if( depth == CV_16U )
func = momentsInTile<ushort, int, int64>;
else if( depth == CV_16S )
func = momentsInTile<short, int, int64>;
else if( depth == CV_32F )
func = momentsInTile<float, double, double>;
else if( depth == CV_64F )
func = momentsInTile<double, double, double>;
else
CV_Error( CV_StsUnsupportedFormat, "" );
Mat src0(mat);
for( int y = 0; y < size.height; y += TILE_SIZE )
{
Size tileSize;
tileSize.height = std::min(TILE_SIZE, size.height - y);
for( int x = 0; x < size.width; x += TILE_SIZE )
{
tileSize.width = std::min(TILE_SIZE, size.width - x);
Mat src(src0, cv::Rect(x, y, tileSize.width, tileSize.height));
if( binary )
{
cv::Mat tmp(tileSize, CV_8U, nzbuf);
cv::compare( src, 0, tmp, CV_CMP_NE );
src = tmp;
}
double mom[10];
func( src, mom );
if(binary)
{
double s = 1./255;
for( int k = 0; k < 10; k++ )
mom[k] *= s;
}
double xm = x * mom[0], ym = y * mom[0];
// accumulate moments computed in each tile
// + m00 ( = m00' )
m.m00 += mom[0];
// + m10 ( = m10' + x*m00' )
m.m10 += mom[1] + xm;
// + m01 ( = m01' + y*m00' )
m.m01 += mom[2] + ym;
// + m20 ( = m20' + 2*x*m10' + x*x*m00' )
m.m20 += mom[3] + x * (mom[1] * 2 + xm);
// + m11 ( = m11' + x*m01' + y*m10' + x*y*m00' )
m.m11 += mom[4] + x * (mom[2] + ym) + y * mom[1];
// + m02 ( = m02' + 2*y*m01' + y*y*m00' )
m.m02 += mom[5] + y * (mom[2] * 2 + ym);
// + m30 ( = m30' + 3*x*m20' + 3*x*x*m10' + x*x*x*m00' )
m.m30 += mom[6] + x * (3. * mom[3] + x * (3. * mom[1] + xm));
// + m21 ( = m21' + x*(2*m11' + 2*y*m10' + x*m01' + x*y*m00') + y*m20')
m.m21 += mom[7] + x * (2 * (mom[4] + y * mom[1]) + x * (mom[2] + ym)) + y * mom[3];
// + m12 ( = m12' + y*(2*m11' + 2*x*m01' + y*m10' + x*y*m00') + x*m02')
m.m12 += mom[8] + y * (2 * (mom[4] + x * mom[2]) + y * (mom[1] + xm)) + x * mom[5];
// + m03 ( = m03' + 3*y*m02' + 3*y*y*m01' + y*y*y*m00' )
m.m03 += mom[9] + y * (3. * mom[5] + y * (3. * mom[2] + ym));
}
}
completeMomentState( &m );
return m;
}
static void momentsInTile( const Mat& img, double* moments )
{
Size size = img.size();
int x, y;
MT mom[10] = {0,0,0,0,0,0,0,0,0,0};
MomentsInTile_SIMD<T, WT, MT> vop;
for( y = 0; y < size.height; y++ )
{
const T* ptr = img.ptr<T>(y);
WT x0 = 0, x1 = 0, x2 = 0;
MT x3 = 0;
x = vop(ptr, size.width, x0, x1, x2, x3);
for( ; x < size.width; x++ )
{
WT p = ptr[x];
WT xp = x * p, xxp;
x0 += p;
x1 += xp;
xxp = xp * x;
x2 += xxp;
x3 += xxp * x;
}
WT py = y * x0, sy = y*y;
mom[9] += ((MT)py) * sy; // m03
mom[8] += ((MT)x1) * sy; // m12
mom[7] += ((MT)x2) * y; // m21
mom[6] += x3; // m30
mom[5] += x0 * sy; // m02
mom[4] += x1 * y; // m11
mom[3] += x2; // m20
mom[2] += py; // m01
mom[1] += x1; // m10
mom[0] += x0; // m00
}
for( x = 0; x < 10; x++ )
moments[x] = (double)mom[x];
}
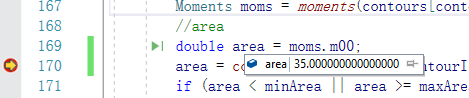
从结果来比较
| Moments moms = moments(contours[contourIdx]); double area = moms.m00; |
double area = contourArea(contours[contourIdx]); |
 |
 |
是一个东西，这样的话就更应该优选contourArea，因为更具有可解释性。但是在这里，使用m00却是有道理的：
因为moms不仅在一个地方被使用，那么这次就算就是非常值的。
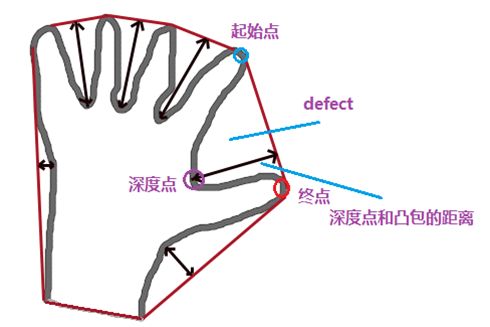
2、凸度的话，从结果图片上再继续分析；
凸度来表示斑点凹凸的程度，其定义为：
 |
简单来说，比如看这张图，area(hull)>>area(contours)，这个值越大，则表明原图这个尖子越多，可以表明是越复杂，越可能存在缺口，越不像一个平滑、规整的图像。
3、惯性里面有一个confidence是什么意思？
if (params.filterByInertia)
{
double denominator = std::sqrt(std::pow(2 * moms.mu11, 2) + std::pow(moms.mu20 - moms.mu02, 2));
const double eps = 1e-2;
double ratio;
if (denominator > eps)
{
double cosmin = (moms.mu20 - moms.mu02) / denominator;
double sinmin = 2 * moms.mu11 / denominator;
double cosmax = -cosmin;
double sinmax = -sinmin;
double imin = 0.5 * (moms.mu20 + moms.mu02) - 0.5 * (moms.mu20 - moms.mu02) * cosmin - moms.mu11 * sinmin;
double imax = 0.5 * (moms.mu20 + moms.mu02) - 0.5 * (moms.mu20 - moms.mu02) * cosmax - moms.mu11 * sinmax;
ratio = imin / imax;
}
else
{
ratio = 1;
}
if (ratio < params.minInertiaRatio || ratio >= params.maxInertiaRatio)
continue;
center.confidence = ratio * ratio;
也就是相当于：
center
.
confidence =
imin
/
imax * (
imin
/
imax)
这个来自于这里的解释：
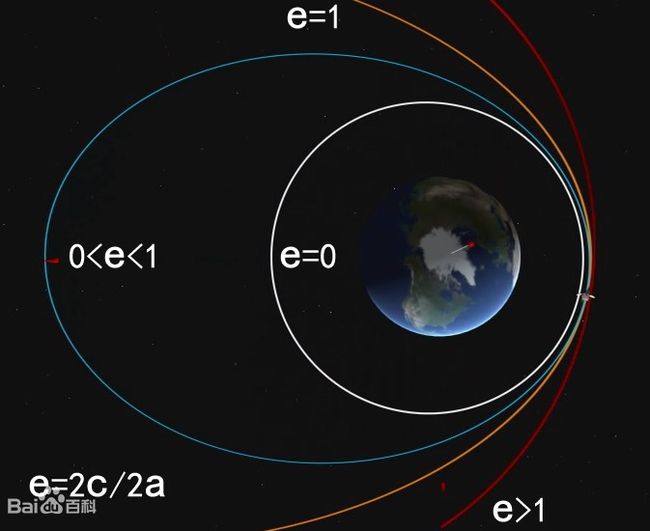
偏心率是指某一椭圆轨道与理想圆形的偏离程度，长椭圆轨道的偏心率高，而近于圆形的轨道的偏心率低。圆形的偏心率等于0，椭圆的偏心率介于0和1之间，而偏心率等于1表示的是抛物线。直接计算斑点的偏心率较为复杂，但利用图像矩的概念计算图形的惯性率，再由惯性率计算偏心率较为方便。偏心率E和惯性率I之间的关系为：
也就是
imin
/
imax
越大，E越小，越解近圆。
惯性率：
偏心率：
偏心率(离心率)
偏心率（Eccentricity）是用来描述圆锥曲线轨道形状的数学量。对于圆锥曲线（二次曲线）的（不完整）统一定义：到定点（焦点）的距离与到定直线（准线）的距离的商是常数e（离心率）的点的轨迹。
当e>1时，为双曲线的一支；当e=1时，为抛物线；当0
对于椭圆，偏心率即为两焦点间的距离（焦距，2c）和长轴长度（2a）的比值，即e=c/a。偏心率反映的是某一椭圆轨道与理想圆环的偏离程度，长椭圆轨道“偏心率”高，而近于圆形的轨道“偏心率”低。
在椭圆的标准方程 (x/a)^2+(y/b)^2=1 中，如果a>b>0焦点在X轴上，这时，a代表长轴、b代表短轴、 c代表两焦点距离的一半，有关系式 c^2=a^2-b^2，即e^2=1-(b/a)^2。因此椭圆偏心率0
4、默认参数不判断圆度，但仍体现出良好的圆的筛选。
默认情况下，是不判断圆度的，但是仍然体现出了良好的对圆的筛选。
/*
* SimpleBlobDetector
*/
SimpleBlobDetector::Params::Params()
{
thresholdStep = 10;
minThreshold = 50;
maxThreshold = 220;
minRepeatability = 2;
minDistBetweenBlobs = 10;
filterByColor = true;
blobColor = 0;
filterByArea = true;
minArea = 25;
maxArea = 5000;
filterByCircularity = false;
minCircularity = 0.8f;
maxCircularity = std::numeric_limits<float>::max();
filterByInertia = true;
//minInertiaRatio = 0.6;
minInertiaRatio = 0.1f;
maxInertiaRatio = std::numeric_limits<float>::max();
filterByConvexity = true;
//minConvexity = 0.8;
minConvexity = 0.95f;
maxConvexity = std::numeric_limits<float>::max();
}
但是它的
Convexity
很高，一般来说，如果要达到这么高的
Convexity
,那么肯定是一个封闭图形；反而也可以直接使用圆度来进行判断，但是得到的结果要少一些。
5、blob和contours的区别、对比
blob和contours是高、低配关系。可以通过代码非常明显地看出,blob调用了contours方法，但仅仅是一种方法；blob在轮廓筛选这块更成熟；但contours还有一个重要的信息，那就是“轮廓间关系”。
将来在使用上，应该推广blob方法，但是可能不仅仅是调用其函数，还是需要将其内容掰开来具体研究分析；对于有“轮廓间
关系
”的情况，应该积极主动使用contours分析。
感谢阅读至此，希望有所帮助。
来自为知笔记(Wiz)