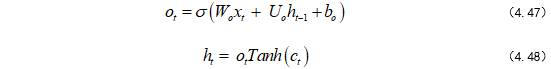1. LSTM原理
由我们所了解的RNN可知，RNN结构之所以出现梯度爆炸或者梯度消失，最本质的原因是因为梯度在传递过程中存在极大数量的连乘，为此有人提出了LSTM模型，它可以对有价值的信息进行记忆，放弃冗余记忆，从而减小学习难度。
与RNN相比，LSTM的神经元还是基于输入X和上一级的隐藏层输出h来计算，只不过内部结构变了，也就是神经元的运算公式变了，而外部结构并没有任何变化，因此上面提及的RNN各种结构都能用LSTM来替换。
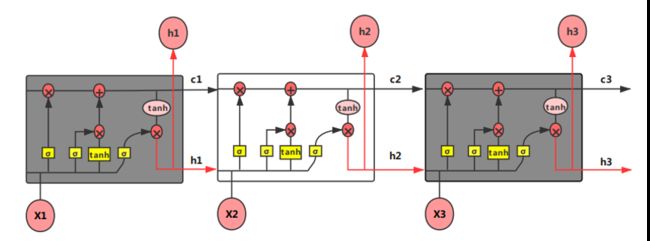
相对于RNN，LSTM的神经元加入了输入门i、遗忘门f、输出门o 和内部记忆单元c。笔者这里先给上一个整体的LSTM结构图如图 4.48所示，之后笔者再对它内部结构的运算逻辑进行详细的解释。
图 4.48 LSTM结构图
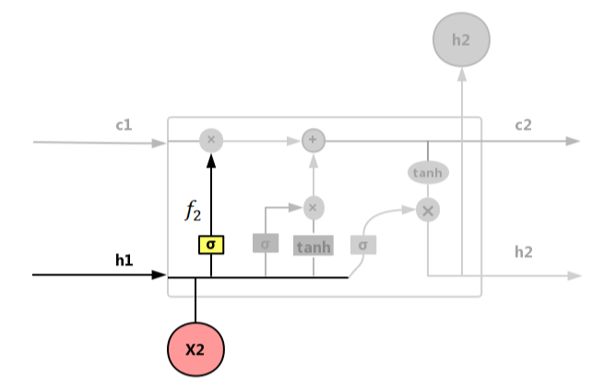
遗忘门f：控制输入X和上一层隐藏层输出h被遗忘的程度大小，如图 4.49所示。
图 4.49 遗忘门(forget gate)
遗忘门公式如式（4.43）：
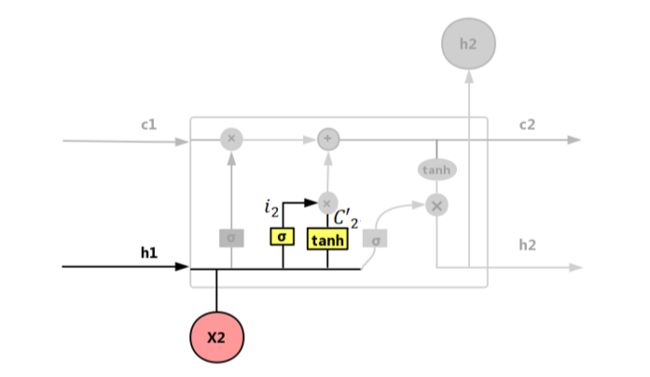
输入门 i：控制输入X和当前计算的状态更新到记忆单元的程度大小，如图 4.50所示。
图 4.50 输入门（input gate）
遗忘门公式如式（4.44）：
内部记忆单元 c：
图 4.51 内部记忆单元
内部记忆单元公式如式（4.45）~（4.46）：
输出门 o：控制输入X和当前输出取决于当前记忆单元的程度大小，如图 4.52所示。
图 4.52 输出门（output gate）
输出门公式如式（4.47）~（4.48）：
其中σ一般选择Sigmoid作为激励函数，主要是起到门控作用。因为Sigmoid函数的输出为0~1，当输出接近0或1时，符合物理意义上的关与开。tanh函数作为生成候选记忆C的选项，因为其输出为-1~1，符合大多数场景下的0中心的特征分布，且梯度（求导）在接近0处，收敛速度比sigmoid函数要快，这也是选择它的另外一个原因。不过LSTM的激励函数也不是一成不变的，大家可以根据自己的需求去更改，只要能更好地解决自己的问题即可。
对于一个训练好的LSTM模型，我们要知道它的每一个门（遗忘门、输出门和输入门）都有各自的(U, W, b)，上述公式也有所体现，这是在训练过程中得到的。而且当输入的序列不存在有用信息时，遗忘门f的值就会接近1，那么输入门i的值接近0，这样过去有用的信息就会被保存。当输入的序列存在重要信息时，遗忘门f的值就会接近0，那么输入门i的值接近1，此时LSTM模型遗忘过去的记忆，记录重要记忆。
因此我们可以看出由遗忘门、输出门、输入门和内部记忆单元共同控制LSTM输出h的设计，使得整个网络更好地把握序列信息之间的关系。
2 BiLSTM介绍
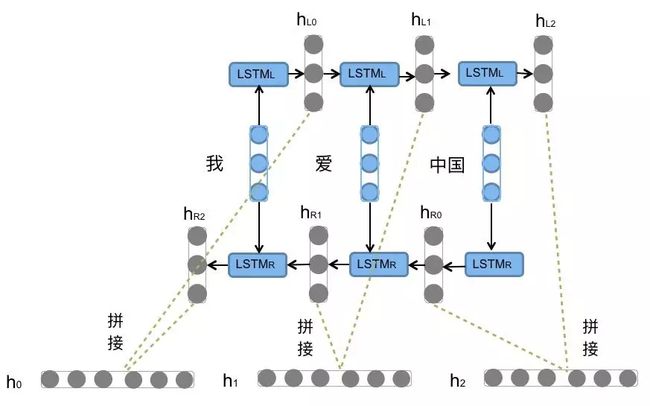
前向的LSTM与后向的LSTM结合成BiLSTM。比如，我们对“我爱中国”这句话进行编码，模型如图6所示。
图6. 双向LSTM编码句子
前向的
依次输入“我”，“爱”，“中国”得到三个向量{
, 
, 
}。后向的
依次输入“中国”，“爱”，“我”得到三个向量{
, 
, 
}。最后将前向和后向的隐向量进行拼接得到{[
, 
], [
, 
], [
, 
]}，即{
, 
, 
}。
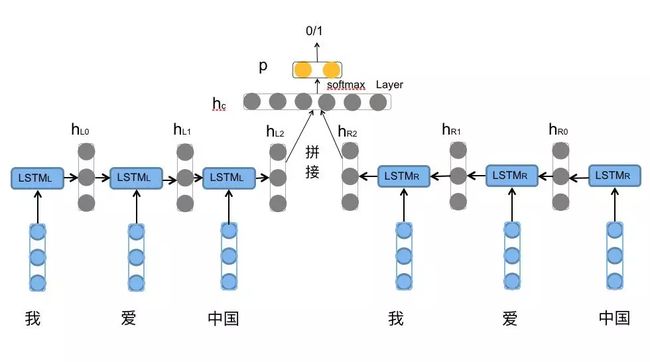
对于情感分类任务来说，我们采用的句子的表示往往是[
, 
]。因为其包含了前向与后向的所有信息，如图7所示。
图7. 拼接向量用于情感分类