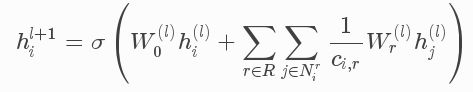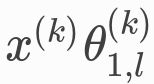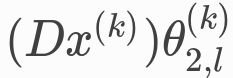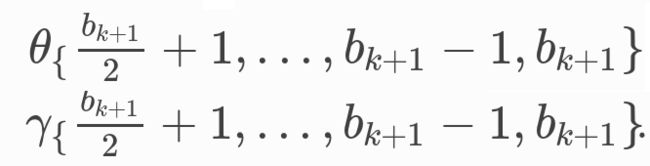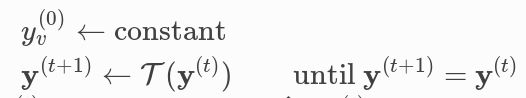Graph Convolutional Networks 图卷积网络
Semi-Supervised Classification with Graph Convolutional Networks 基于图卷积网络的半监督分类
原文：https://arxiv.org/abs/1609.02907
参考：https://blog.csdn.net/w986284086/article/details/80270653
DGL 实现：https://docs.dgl.ai/tutorials/models/1_gnn/1_gcn.html
DGL 实现（ZACHARY空手道俱乐部网络）: https://docs.dgl.ai/tutorials/basics/1_first.html
Graph and “Zachary’s karate club” problem
图的基本概念
- 顶点（vertex）
- 边（edge）
- 有向/无向图（Directed Graph / Undirected Graph）
- 边的权重（weight）
- 路径/最短路径（path / shortest path）
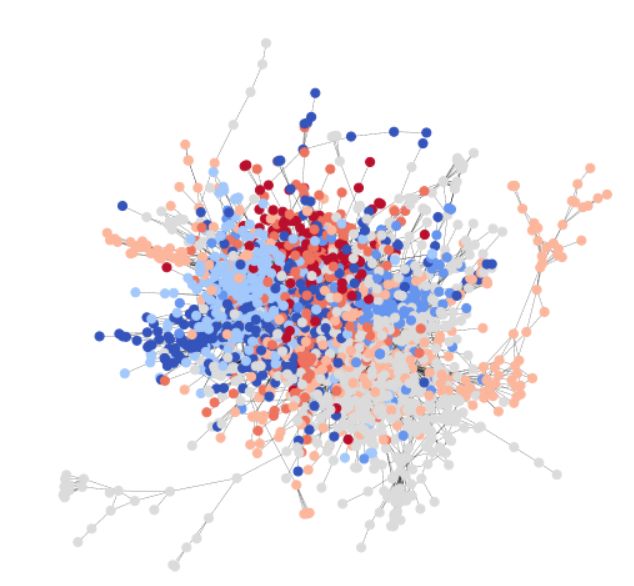
空手道俱乐部数据集
- 顶点：一个俱乐部成员
- 边：成员之间在俱乐部以外的关系
- 无向，所有权重相同
- 问题：以教练（0）和主席（33）两个人为首，将整个俱乐部分为两个派别
对一个节点的卷积
-
与某节点相邻的所有节点，对所有特征向量求和，表示为：
-
线性+非线性变换：
Graph Attention Networks 图注意力网络
原文：https://arxiv.org/abs/1710.10903
参考：https://www.cnblogs.com/chaoran/p/9720708.html
参考：https://www.cnblogs.com/wangxiaocvpr/p/7889307.html
参考：https://blog.csdn.net/b224618/article/details/81407969
DGL 实现：https://github.com/dmlc/dgl/tree/master/examples/pytorch/gat
线性变换
所有 node 共用一个 W 作 feature 的线性变换，变换后 F 和 F‘ 可以不同
N 为node 数量, F 为每个node 的 feature 数（feature vector 长度）
-
输入：
-
输出：
计算 attention coefficients
表示 node j 的 feature 对 node i 的重要性：
函数a：一个单层前馈网络 torch.bmm(head_ft, self.attn_l)
卷积
多头注意力
设置 K 个函数，计算出 K 组attention coefficient，连接K个输出：
对于最后一个卷积层，连接改为求平均：
Modeling Relational Data with Graph Convolutional Networks
原文：https://arxiv.org/abs/1703.06103
参考：https://lanzhuzhu.github.io/2017/04/30/IE/RelationExtraction/Modeling%20Relational%20Datawith%20Graph%20Convolutional%20Networks/
DGL 实现：https://docs.dgl.ai/tutorials/models/1_gnn/4_rgcn.html
普通GCN（本文第一种）利用图的结构来提取每个节点的特征，没有利用图的边。知识图谱以三元组（主体、客体和主客体之间的关系）为单位组成，因此图的边编码了重要的关系信息。而且每对节点之间可能存在多条边（对应多种关系）。
在统计关系学习（statistical relational learning, SRL）中，有两种任务，都需要从图的相邻结构中恢复丢失的信息：
- 实体分类（Entity classification），例如将实体分为某种类别，并赋予该类别中的一些特征
- 连接预测（Link prediction），例如推断某个缺失的三元组
例如知道了“小明在北京大学读书”，就能知道“小明”应该被归类为“人类”，而且知识图谱中一定有（小明，住在，中国）这样一个三元组。
R-GCN用一个图卷积网络同时解决了上述两种问题：
- 实体分类：每个节点最后使用softmax输出
- 连接预测：利用自编码器结构重建图的边
回忆一下，普通GCN的卷积操作如下：
R-GCN的卷积操作如下：
其区别在于R-GCN中，通往一个节点的不同边可以代表不同的关系。在普通GCN中，所有边共享相同的权重 W ；在R-GCN中，不同类型的边（关系）使用不同的权重 Wr ，只有同一种边（关系）才会使用同一个权重。
“不同关系对应不同权重”的做法大大增加了模型的参数量，原文使用了基分解（basis decomposition）来降低参数量和防止过拟合：
此处的 V 为基， a 为coefficient，基的数目 B 远小于数据中的关系数目
Supervised Community Detection with Line Graph Neural Networks
原文：https://arxiv.org/abs/1705.08415
DGL 实现：https://docs.dgl.ai/tutorials/models/1_gnn/6_line_graph.html
开头的GCN完成了对每个节点的分类，这里的LGNN则是对图中的节点进行聚类（“社区发现”，community detection）。这个模型的一个亮点在于将普通GCN应用在线图（line graph）中
CORA：科技论文数据集
- 节点：2708篇论文，分为7个不同机器学习领域
- 有向边：论文之间的引用关系
-
问题：通过监督学习对论文进行分类
线图
将一个老图的边，作为一个新图的节点，画出来的图。下图中的蓝点和黑线是一个老有向图，红点既是老图的边、也是新图的节点。将相邻的红点按老边的方向有方向地连起来，就得到一个线图。
LGNN（这里的计算我没有看懂）
在LGNN中有若干层，每一层的图（x）和其线图（y）在数据流中的变化过程如下图：
在图表征（x）中，第 k 层、第 l 个通道的第 i 个节点按以下公式进行 k+1 层的更新：
类似地，线图（y）中的运算为：
等号的右边可分为五部分：
-
x的线性变换
-
a linear projection of degree operator ( linear map D:F→DF where (Dx)i:=deg(i)·xi, D(x) =diag(A1)x .)on x,
-
a summation of 2j adjacency operator (linear map given by the adjacency matrix Ai,j= 1if f(i,j)∈E.) on x
-
fusing another graph’s embedding information using incidence matrix {Pm,Pd}, followed with a linear projection
-
skip-connection：将前面的非线性函数ρ换为线性变换
Stochastic Steady-state Embedding (SSE)
原文：http://proceedings.mlr.press/v80/dai18a/dai18a.pdf
DGL 实现：https://docs.dgl.ai/tutorials/models/1_gnn/8_sse_mx.html
Flood-fill / Infection algorithm（Steady-state algorithms）
在图 G=(V,E) 中，有 起始节点 s ∈ V，
设 V = {1,...,n}，yv 为节点 v 是否被标记，N(v) 为 v 的所有相邻节点（包括v本身）
对图中可以到达 s 的所有节点进行标记：
当（2）迭代足够次数后，所有可以到达 s 的节点都被标记，我们说达到了稳态（steady state）
Steady-state operator
上述过程可抽象为：
其中
在 flood-fill 算法中，T^=max
因为当且仅当 y∗=T(y∗) 时，y 在 T 下达到稳态，所以称 T 为 steady-state operator
Neural flood-fill algorithm（Steady-state embedding）
用神经网络模拟 flood-fill algorithm
- 用图神经网络 TΘ ,来代替 T
- 用向量 hv（维度为H），来代替 布尔值yv
- 为节点 v 赋予一个特征向量 xv（在 flood-fill 算法中，xv为每个节点编号的 one-hot code，用于区分不同节点）
- 只迭代有限次数，不一定达到稳态
- 迭代结束后，以 hv 为输入，每个节点可以被到达的概率为输出，训练另一个神经网络
上述过程可写成：
