Java的递归以及八皇后问题
递归
简单来说递归就是函数自己调用自己,但是这样理解会比较抽象,打个比方就是俄罗斯套娃,一个套一个
递归也需要有自己的中止判断条件,否则会一直递归下去,无限循环。
根据代码来理解会比较好理解。
递归求阶乘:
public static int test(int n) {
if (n == 1) {
return 1;
}else if (n>0){
int ans = test(n - 1) * n;
return ans;
}else {
return 1;
}
}
中止条件是 n == 0,当n=0时退出循环,ans实际上就是n(n-1)...21,达到递归的效果
迷宫回溯问题,寻找可达路径
用递归来实现,分别给四个方向上加减1,设迷宫没有走过的路径为0,墙体,障碍为1,走过而且能走通的路径为2,走不通的路径为3
代码实现如下:
package Ivan.recursion;
public class Maze {
public static void main(String[] args) {
//二维数组创建迷宫
int[][] map = new int[8][7];
//1为墙
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//设置路障
map[3][1] = 1;
map[3][2] = 1;
//输出地图
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j]);
}
System.out.println();
}
//使用递归给小球找路
findWay(map, 1, 1);
//输出小球走过的地图
System.out.println("小球走过的路径");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j]);
}
System.out.println();
}
}
/**
* @param map 地图
* @param i 小球起始横坐标
* @param j 小球起始纵坐标
* @return 找到通路返回true,否则返回false
*/
//设map[6][5]为终点
//约定1为墙,2为通路,3为走过但走不通,0为没有走过
public static boolean findWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) {
map[i][j] = 2; //假定这点能走通
if (findWay(map, i + 1, j)) { //向下走
return true;
} else if (findWay(map, i, j + 1)) { //向下走
return true;
} else if (findWay(map, i + 1, j)) { //向左走
return true;
} else if (findWay(map, i, j - 1)) {
return true;
} else {
//说明该点走不通
map[i][j] = 3;
return false;
}
} else {
//如果map[i][j] != 0
return false;
}
}
}
}
看代码理解即可,如果四个方向都没有办法走通,那么设置这个位置为3,回溯,代码运行成果如图
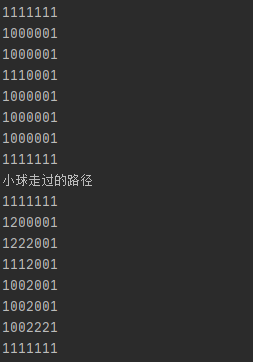
八皇后问题
八皇后简述
八皇后问题,一个古老而著名的问题,是回溯算法的典型案例。
该问题由国际西洋棋棋手马克斯·贝瑟尔于 1848 年提出:在 8×8 格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
题目理解
从题目中可以理解到,棋盘为8x8,两个皇后不能处于同一行,那么就意味着每行只能放置一个皇后,就没有必要使用二维数组去模拟这个问题。
把每个皇后的位置放在数组中,arr[7],arr[0] = i,就说明第零行,第i列的位置可以放置皇后。
再对皇后放置的位置合理性进行判断
设当前位置为i,前面总共放了n个皇后
1.不能在同一行————用一维数组模拟就可以避免这个问题
2.不能在同一列————a[n]!=a[i]
3.不能在同意斜线上————两个皇后连线的斜率!=1,引入Math包,Math.abs(n-i) != Math.abs(arr[n] - arr[i)
代码如下:
package Ivan.recursion;
public class Queen8 {
//定义一个max表示共有多少个皇后
int max = 8;
//数组arr存放皇后放置位置
int[] arr = new int[max];
public static void main(String[] args) {
Queen8 queen8 = new Queen8();
queen8.check(0);
}
//放置第n个皇后
public void check(int n) {
if (n == max){
print();
return;
}
for (int i = 0; i < max; i++) {
//先把当前的皇后n,放到该行的第一列
arr[n] = i;
if (judge(n)){
//不冲突则继续放
check(n+1);
}
//冲突则继续执行arr[n] = i;即第n个皇后放在本行的后移的一个位置
}
}
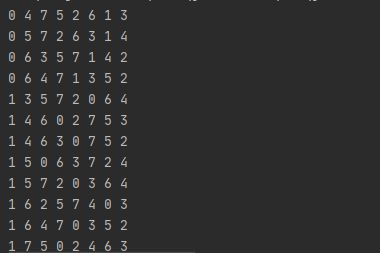
private void print() {
for (int i = 0; i < arr.length; i++) {
System.out.printf(arr[i]+" ");
}
System.out.println();
}
//判断当前位置是否冲突
/**
* @param n 表示第n个皇后
* @return 表示位置是否合理
*/
public boolean judge(int n) {
for (int i = 0; i < n; i++) {
//arr[i] == arr[n]表示第n个皇后和第i个皇后是否在同一列
//Math.abs(n-i) == Math.abs(arr[n]-arr[i])表示第n个皇后和第i个皇后是否在同一斜线 斜率
if (arr[i] == arr[n] || Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
return false;
}
}
return true;
}
}