为什么java Hashmap 中的加载因子是默认为0.75
转自:http://www.jianshu.com/p/dff8f4641814
前几天在一个群里看到有人讨论hashmap中的加载因子为什么是默认0.75。
HashMap源码中的加载因子
static final float DEFAULT_LOAD_FACTOR = 0.75f; 当时想到的是应该是“哈希冲突”和“空间利用率”矛盾的一个折衷。
跟数据结构要么查询快要么插入快一个道理,hashmap就是一个插入慢、查询快的数据结构。
加载因子是表示Hsah表中元素的填满的程度。
加载因子越大,填满的元素越多,空间利用率越高,但冲突的机会加大了。
反之,加载因子越小,填满的元素越少,冲突的机会减小,但空间浪费多了。
冲突的机会越大,则查找的成本越高。反之,查找的成本越小。
因此,必须在 "冲突的机会"与"空间利用率"之间寻找一种平衡与折衷。
但是为什么一定是0.75?而不是0.8,0.6
本着不嫌事大的精神继续深挖,在此之前先简单补充点本文需要的基础知识:
1.冲突定义:假设哈希表的地址集为[0,n),冲突是指由关键字得到的哈希地址为j(0<=j<=n-1)的位置上已经有记录。在关键字得到的哈希地址上已经有记录,那么就称之为冲突
2.处理冲突:就是为该关键字的记录扎到另一个“空”的哈希地址。即在处理哈希地址的冲突时,若得到的另一个哈希地址H1仍然发生冲突,则再求下一个地址H2,若H2仍然冲突,再求的H3,直至Hk不发生冲突为止,则Hk为记录在表中的地址。
处理冲突的几种方法:
一、 开放定址法
Hi=(H(key) + di) MOD m i=1,2,...k(k<=m-1)其中H(key)为哈希函数;m为哈希表表长;di为增量序列。
开放定址法根据步长不同可以分为3种:
1)线性探查法(Linear Probing):di=1,2,3,...,m-1
简单地说就是以当前冲突位置为起点,步长为1循环查找,直到找到一个空的位置就把元素插进去,循环完了都找不到说明容器满了。就像你去一条街上的店里吃饭,问了第一家被告知满座,然后挨着一家家去问是否有位置一样。
2)线性补偿探测法:di=Q 下一个位置满足 Hi=(H(key) + Q) mod m i=1,2,...k(k<=m-1) ,要求 Q 与 m 是互质的,以便能探测到哈希表中的所有单元。
继续用上面的例子,现在你不是挨着一家家去问了,拿出计算器算了一下,然后隔Q家问一次有没有位置。
3)伪随机探测再散列:di=伪随机数序列。还是那个例子,这是完全根据心情去选一家店来问了
缺点:
- 这种方法建立起来的hash表当冲突多的时候数据容易堆聚在一起,这时候对查找不友好;
- 删除结点不能简单地将被删结 点的空间置为空,否则将截断在它之后填人散列表的同义词结点的查找路径。因此在 用开放地址法处理冲突的散列表上执行删除操作,只能在被删结点上做删除标记,而不能真正删除结点
- 当空间满了,还要建立一个溢出表来存多出来的元素。
二、再哈希法
Hi = RHi(key),i=1,2,...k
RHi均是不同的哈希函数,即在同义词产生地址冲突时计算另一个哈希函数地址,直到不发生冲突为止。这种方法不易产生聚集,但是增加了计算时间。
缺点:增加了计算时间。
三、建立一个公共溢出区
假设哈希函数的值域为[0,m-1],则设向量HashTable[0...m-1]为基本表,每个分量存放一个记录,另设立向量OverTable[0....v]为溢出表。所有关键字和基本表中关键字为同义词的记录,不管他们由哈希函数得到的哈希地址是什么,一旦发生冲突,都填入溢出表。
简单地说就是搞个新表存冲突的元素。
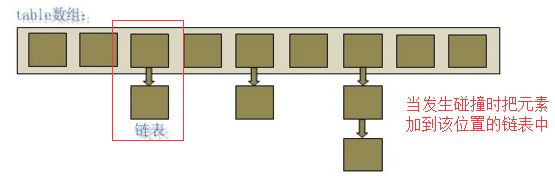
四、链地址法(拉链法)
将所有关键字为同义词的记录存储在同一线性链表中,也就是把冲突位置的元素构造成链表。
拉链法的优点:
- 拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;
- 由于拉链法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况;
- 在用拉链法构造的散列表中,删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。
拉链法的缺点:
- 指针需要额外的空间,故当结点规模较小时,开放定址法较为节省空间,而若将节省的指针空间用来扩大散列表的规模,可使装填因子变小,这又减少了开放定址法中的冲突,从而提高平均查找速度
Java中HashMap的数据结构
HashMap实际上是一个“链表散列”的数据结构,即数组和链表的结合体。
看图就可以知道Java中的hashMap使用了拉链法处理冲突。
HashMap有一个初始容量大小,默认是16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16为了减少冲突的概率,当hashMap的数组长度到了一个临界值就会触发扩容,把所有元素rehash再放到扩容后的容器中,这是一个非常耗时的操作。
而这个临界值由【加载因子】和当前容器的容量大小来确定:DEFAULT_INITIAL_CAPACITY*DEFAULT_LOAD_FACTOR ,即默认情况下是16x0.75=12时,就会触发扩容操作。
所以使用hash容器时尽量预估自己的数据量来设置初始值。具体代码实现自行去研究HashMap的源码。
基础知识补充完毕,回到正题,为什么加载因子要默认是0.75?
从hashmap源码注释里找到了这一段
Ideally, under random hashCodes, the frequency of
- nodes in bins follows a Poisson distribution
- (http://en.wikipedia.org/wiki/Poisson_distribution) with a
- parameter of about 0.5 on average for the default resizing
- threshold of 0.75, although with a large variance because of
- resizing granularity. Ignoring variance, the expected
- occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
- factorial(k)). The first values are:
- 0: 0.60653066
- 1: 0.30326533
- 2: 0.07581633
- 3: 0.01263606
- 4: 0.00157952
- 5: 0.00015795
- 6: 0.00001316
- 7: 0.00000094
- 8: 0.00000006
- more: less than 1 in ten million
注意wiki链接中的关键字:Poisson_distribution
泊淞分布啊
简单翻译一下就是在理想情况下,使用随机哈希码,节点出现的频率在hash桶中遵循泊松分布,同时给出了桶中元素个数和概率的对照表。
从上面的表中可以看到当桶中元素到达8个的时候,概率已经变得非常小,也就是说用0.75作为加载因子,每个碰撞位置的链表长度超过8个是几乎不可能的。
好了,再深挖就要挖到统计学那边去了,就此打住,重申一下使用hash容器请尽量指定初始容量,且是2的幂次方。
关于泊淞分布的知识请看
http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html#comment-356111
欢迎讨论,这个周末的任务完成了,可以放心去浪了─=≡Σ((( つ•̀ω•́)つ超人